Teoria informacji/TI Wykład 5: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 3: | Linia 3: | ||
{{definicja|[Entropia zmiennej losowej]|entropia2| | {{definicja|[Entropia zmiennej losowej]|entropia2| | ||
Jeśli <math>X: S \to {\mathcal X}</math> jest zmienną losową, określamy jej entropię jako | Jeśli <math>X: S \to {\mathcal X}</math> jest zmienną losową, określamy jej entropię jako | ||
<center><math>H_r (X) = \sum_{t \in {\mathcal X}} p (X = t) \cdot \log_r \frac{1}{p (X = t)}</math></center>}} | |||
Innymi słowy, <math>H_r(X)</math> jest równe wartości oczekiwanej | Innymi słowy, <math>H_r(X)</math> jest równe wartości oczekiwanej | ||
<center><math>H_r (X) = E \left( \log_r \frac{1}{p (X)} \right)</math></center> | |||
gdzie ''p(X) '' jest zmienną losową na ''S'' zdefiniowaną jako <math>p(X): s \mapsto p (X = X(s))</math> | gdzie ''p(X) '' jest zmienną losową na ''S'' zdefiniowaną jako <math>p(X): s \mapsto p (X = X(s))</math> | ||
<center><math>\sum_{t \in {\mathcal X}} p (X = t) \cdot \log_r \frac{1}{p (X = t)} = \sum_{t \in {\mathcal X}} \sum_{X(s) = t} p(s) \cdot \frac{1}{p (X = t)} = \sum_{s \in S} p(s) \cdot \frac{1}{p (X = X(s))}</math></center> | |||
| Linia 17: | Linia 17: | ||
{{definicja|[Entropia warunkowa]|entropia_warunkowa| Niech <math>A : S \to {\mathcal A}</math>,<math>B : S \to {\mathcal B}</math> będą dwiema zmiennymi losowymi. Dla <math>b \in {\mathcal B}</math> określamy | {{definicja|[Entropia warunkowa]|entropia_warunkowa| Niech <math>A : S \to {\mathcal A}</math>,<math>B : S \to {\mathcal B}</math> będą dwiema zmiennymi losowymi. Dla <math>b \in {\mathcal B}</math> określamy | ||
<center><math>H_r (A | b) = \sum_{a \in {\mathcal A}} p(a|b) \cdot \log_r \frac{1}{p (a|b)}</math></center> | |||
i ogólnie | i ogólnie | ||
<center><math>H_r (A | B) = \sum_{b \in {\mathcal B}} p(b) H_r (A | b)</math>.</center> | |||
Powyższą wartość nazywamy '''entropią warunkową A od B'''}} | Powyższą wartość nazywamy '''entropią warunkową A od B'''}} | ||
| Linia 26: | Linia 26: | ||
Zauważmy że jeśli ''A'' i ''B'' są niezależne, to w powyższej formule <math>p(a|b)=a</math> a więc <math>H_r(A|B)=A</math>. Z drugiej strony <math>H_r(A|A)=0</math>. Ogólnie dla dowolnej funkcji <math>\varphi : {\mathcal A} \to {\mathcal B}</math> mamy | Zauważmy że jeśli ''A'' i ''B'' są niezależne, to w powyższej formule <math>p(a|b)=a</math> a więc <math>H_r(A|B)=A</math>. Z drugiej strony <math>H_r(A|A)=0</math>. Ogólnie dla dowolnej funkcji <math>\varphi : {\mathcal A} \to {\mathcal B}</math> mamy | ||
<center><math>H_r (\varphi ( A) | A) = 0</math></center> | |||
Rzeczywiście, jeśli <math>p(A=a)>0</math> to <math>p (\varphi ( A) = \varphi (a) | A = a ) = 1</math>, i w konsekwencji <math>\log_r \frac{1}{p (\varphi ( A) = \varphi (a) | A = a )} = 0</math>. | Rzeczywiście, jeśli <math>p(A=a)>0</math> to <math>p (\varphi ( A) = \varphi (a) | A = a ) = 1</math>, i w konsekwencji <math>\log_r \frac{1}{p (\varphi ( A) = \varphi (a) | A = a )} = 0</math>. | ||
'''Entropia łączna''' | '''Entropia łączna''' | ||
Będziemy również rozważać pary ''(A,B) '' jako jedną zmienną losową <math>(A,B): S \to {\mathcal A} \times {\mathcal B}</math>, | Będziemy również rozważać pary ''(A,B) '' jako jedną zmienną losową <math>(A,B): S \to {\mathcal A} \times {\mathcal B}</math>, | ||
<center><math>(A,B) (s) = \left( A(s), B(s) \right)</math></center> | |||
Prawdopodobieństwo że ta zmienna przyjmie wartość ''(a,b)'' wynosi <math>p \left( (A,B) = (a,b) \right) = p \left( (A = a) \wedge (B = b) \right)</math>, co zapisujemy w skrócie jako <math>p(a \and b)</math>. To prawdopodobieństwo w ogólności jest inne niż <math>p(a) \cdot p(b)</math>. Jeśli dla dowolnych <math>a \in {\mathcal A}, b \in {\mathcal B}</math> | Prawdopodobieństwo że ta zmienna przyjmie wartość ''(a,b)'' wynosi <math>p \left( (A,B) = (a,b) \right) = p \left( (A = a) \wedge (B = b) \right)</math>, co zapisujemy w skrócie jako <math>p(a \and b)</math>. To prawdopodobieństwo w ogólności jest inne niż <math>p(a) \cdot p(b)</math>. Jeśli dla dowolnych <math>a \in {\mathcal A}, b \in {\mathcal B}</math> | ||
| Linia 38: | Linia 39: | ||
Entropia <math>H_r(A,B)</math> wprost z definicji wynosi | Entropia <math>H_r(A,B)</math> wprost z definicji wynosi | ||
<center><math>H_r (A,B) = \sum_{a \in {\mathcal A}, b \in {\mathcal B}} p ( a \wedge b) \cdot \log_r \frac{1}{p( a \wedge b)}</math></center> | |||
Jeśli ''A'' i ''B'' są niezależne, to | Jeśli ''A'' i ''B'' są niezależne, to | ||
<center><math>\log_r \frac{1}{p (A,B)} = \log_r \frac{1}{p (A)} + \log_r \frac{1}{p (B)}</math></center> | |||
Z liniowości wartości oczekiwanej dostajemy wtedy | Z liniowości wartości oczekiwanej dostajemy wtedy | ||
<center><math>H_r (A,B) = H_r (A) + H_r (B)</math></center> | |||
| Linia 50: | Linia 51: | ||
{{twierdzenie||do_łącznej| | {{twierdzenie||do_łącznej| Dla dowolnych A i B zachodzi | ||
<center><math>H_r (A,B) \leq H_r (A) + H_r (B)</math></center> | |||
i równość zachodzi jedynie gdy ''A'' i ''B'' są niezależne.}} | i równość zachodzi jedynie gdy ''A'' i ''B'' są niezależne.}} | ||
{{dowod||| Rozpiszemy prawą stronę tak żebyśmy mogli użyć Złotego Lematu. Użyjemy w tym celu oczywistych równości <math>p(a) =\sum_{b \in {\mathcal B}} p( a \wedge b) </math> i <math>p(b) = \sum_{a \in {\mathcal A}} p( a \wedge b)</math>. | {{dowod||| Rozpiszemy prawą stronę tak żebyśmy mogli użyć Złotego Lematu. Użyjemy w tym celu oczywistych równości | ||
<math>H_r (A) + H_r (B) = \sum_{a \in {\mathcal A}} p (a) \log_r \frac{1}{p(a)} | <math>p(a) = \sum_{b \in {\mathcal B}} p( a \wedge b) </math> i <math>p(b) = \sum_{a \in {\mathcal A}} p( a \wedge b)</math>. | ||
+ \sum_{b \in {\mathcal B}} p(b) \log_r \frac{1}{p(b)} | <center><math>\aligned | ||
H_r (A) + H_r (B) & = \sum_{a \in {\mathcal A}} p (a) \log_r \frac{1}{p(a)} | |||
+ \sum_{b \in {\mathcal B}} \sum_{a \in {\mathcal A}} p( a \wedge b) \log_r \frac{1}{p(b)} | + \sum_{b \in {\mathcal B}} p(b) \log_r \frac{1}{p(b)}\\ | ||
& = \sum_{a \in {\mathcal A}} \sum_{b \in {\mathcal B}} p( a \wedge b) \log_r \frac{1}{p(a)} | |||
+ \sum_{b \in {\mathcal B}} \sum_{a \in {\mathcal A}} p( a \wedge b) \log_r \frac{1}{p(b)}\\ | |||
& = \sum_{a \in {\mathcal A}, b \in {\mathcal B}} p( a \wedge b) \log_r \frac{1}{p(a)p(b)} | |||
\endaligned | |||
</math></center> | |||
Ważne że powyższe wyrażenie jest dobrze zdefiniowane, bo gdy <math>p(a)=0</math> lub <math>p(b)=0</math>, to również <math>p(a \and b)=0</math>. | Ważne że powyższe wyrażenie jest dobrze zdefiniowane, bo gdy <math>p(a)=0</math> lub <math>p(b)=0</math>, to również <math>p(a \and b)=0</math>. | ||
Oznaczmy chwilowo | Oznaczmy chwilowo | ||
<center><math>({\mathcal A} \times {\mathcal B})^{+} = \{ (a,b) : p(a) > 0 \mbox{ i } p(b) > 0 \}</math></center> | |||
Mamy wtedy | Mamy wtedy | ||
<center><math>\sum_{ (a,b) \in ({\mathcal A} \times {\mathcal B})^{+}} p( a \wedge b) = \sum_{ (a,b) \in ({\mathcal A} \times {\mathcal B})^{+}} p(a)\cdot p(b)= 1</math>.</center> | |||
Używając Złotego Lematu dla <math>x=p(a \and b)</math>, <math>y=p(a)\cdot p(b)</math> dla wszystkich <math>(a,b) \in ({\mathcal A} \times {\mathcal B})^{+}</math> otrzymujemy | Używając [[Teoria informacji/TI Wykład 2#złoty|Złotego Lematu]] dla <math>x=p(a \and b)</math>, <math>y=p(a)\cdot p(b)</math> dla wszystkich <math>(a,b) \in ({\mathcal A} \times {\mathcal B})^{+}</math> otrzymujemy | ||
<math>H_r (A,B) = \sum_{ (a,b) \in ({\mathcal A} \times {\mathcal B})^{+}} p( a \wedge b) \log_r \frac{1}{p( a \wedge b)} | <center><math>\aligned | ||
H_r (A,B) & = \sum_{ (a,b) \in ({\mathcal A} \times {\mathcal B})^{+}} p( a \wedge b) \log_r \frac{1}{p( a \wedge b)}\\ | |||
& \leq \sum_{ (a,b) \in ({\mathcal A} \times {\mathcal B})^{+}} p( a \wedge b) \log_r \frac{1}{p(a)p(b) }\\ | |||
& = H_r (A) + H_r (B) | |||
\endaligned | |||
</math></center> | |||
Dodatkowo równość zachodzi wyłącznie gdy <math>p(a \and b) = p(a) \cdot p(b)</math> dla wszystkich <math> (a,b) \in ({\mathcal A} \times {\mathcal B})^{+}</math> (czyli w ogóle dla wszystkich <math> a \in {\mathcal A}, b \in {\mathcal B}</math>. W drugą stronę, wiemy już że niezależność A i B implikuje tutaj równość.}} | Dodatkowo równość zachodzi wyłącznie gdy <math>p(a \and b) = p(a) \cdot p(b)</math> dla wszystkich <math> (a,b) \in ({\mathcal A} \times {\mathcal B})^{+}</math> (czyli w ogóle dla wszystkich <math> a \in {\mathcal A}, b \in {\mathcal B}</math>. W drugą stronę, wiemy już że niezależność A i B implikuje tutaj równość.}} | ||
| Linia 79: | Linia 87: | ||
{{definicja|[Informacja]|informacja|Wartość | {{definicja|[Informacja]|informacja|Wartość | ||
<center><math>I(A;B) = H_r (A) + H_r (B) - H_r (A,B)</math></center> | |||
nazywamy '''informacją wzajemną''' zmiennych A i B.}} | nazywamy '''informacją wzajemną''' zmiennych A i B.}} | ||
| Linia 89: | Linia 97: | ||
'''Komentarz''' Przekształcając definicję informacji analogicznie jak w ostatnim dowodzie, otrzymujemy: | '''Komentarz''' Przekształcając definicję informacji analogicznie jak w ostatnim dowodzie, otrzymujemy: | ||
<center><math>I(A;B) = \sum_{a \in {\mathcal A}, b \in {\mathcal B}} p( a \wedge b) \left( \log \frac{1}{p(a)p(b) } - \log \frac{1}{p( a \wedge b)} \right)</math></center> | |||
<math>I(A;B) = \sum_{a \in {\mathcal A}, b \in {\mathcal B}} p( a \wedge b) \left( \log \frac{1}{p(a)p(b) } - \log \frac{1}{p( a \wedge b)} \right)</math> | |||
W takiej postaci widać że informacja jest pewną miarą odległości pomiędzy faktycznym rozkładem zmiennej (A;B), a jej rozkładem gdyby A i B były niezależne. | W takiej postaci widać że informacja jest pewną miarą odległości pomiędzy faktycznym rozkładem zmiennej (A;B), a jej rozkładem gdyby A i B były niezależne. | ||
| Linia 100: | Linia 107: | ||
{{fakt|[Zasada łańcuchowa]|łańcuch| | {{fakt|[Zasada łańcuchowa]|łańcuch| Dla dowolnych A i B zachodzi | ||
<center><math>H(A,B)=H(A|B)+H(B)</math></center>}} | |||
{{dowod||dw_łańcuch|Obliczamy: | {{dowod||dw_łańcuch|Obliczamy: | ||
<math>H | <center><math>\aligned | ||
H(A,B) & = \sum_{a \in {\mathcal A}, b \in {\mathcal B}} p ( a \wedge b) \cdot \log \frac{1}{p( a \wedge b)}\\ | |||
& = \sum_{a \in {\mathcal A}} \sum_{b \in {\mathcal B}} p(a|b) p(b) \cdot \log \frac{1}{p(a|b) p(b)} \\ | |||
\cdot \log \frac{1}{p(a|b) p(b)} | & = \sum_{a \in {\mathcal A}} \sum_{b \in {\mathcal B}} p(a|b) p(b) \cdot \left( \log \frac{1}{p(a|b)} + \log \frac{1}{p(b)} \right)\\ | ||
& = \sum_{b \in {\mathcal B}} p(b) \cdot \sum_{a \in {\mathcal A}} p(a|b) \cdot \log \frac{1}{p(a|b)} + \sum_{b \in {\mathcal B}} p(b) \log \frac{1}{p(b)} \cdot \sum_{a \in {\mathcal A}} p(a|b) \\ | |||
& = H(A|B) + H(B) | |||
\cdot \left( \log \frac{1}{p(a|b)} + \log \frac{1}{p(b)} \right) | \endaligned | ||
</math></center>}} | |||
p(a|b) \cdot \log \frac{1}{p(a|b)} + \sum_{b \in {\mathcal B}} p(b) \log \frac{1}{p(b)} \cdot \sum_{a \in {\mathcal A}} p(a|b) | |||
Używając zasady łańcuchowej, możemy wyliczać informację na różne sposoby: | Używając zasady łańcuchowej, możemy wyliczać informację na różne sposoby: | ||
<math>I(A;B)=H(A)-H(A|B)=H(B)-H(B|A)</math> | <center><math>I(A;B)=H(A)-H(A|B)=H(B)-H(B|A)</math></center> | ||
Kolejną rzeczą jaką możemy zauważyć to <math>I(A;B) \leq \min \{H(A), H(B)\}</math> | Kolejną rzeczą jaką możemy zauważyć to <math>I(A;B) \leq \min \{H(A), H(B)\}</math> | ||
| Linia 126: | Linia 129: | ||
Łatwo możemy też uogólnić zasadę łańcuchową na przypadek <math>n \ge 2</math> zmiennych <math>A_1, A_2, \ldots , A_n</math> | Łatwo możemy też uogólnić zasadę łańcuchową na przypadek <math>n \ge 2</math> zmiennych <math>A_1, A_2, \ldots , A_n</math> | ||
<math>H(A_1, \ldots , A_n ) = H(A_1 | A_2, \ldots , A_n ) + H(A_2, \ldots , A_n ) | <center><math>\aligned | ||
H(A_1, \ldots , A_n ) & = H(A_1 | A_2, \ldots , A_n ) + H(A_2, \ldots , A_n ) \\ | |||
& = H(A_1 | A_2, \ldots , A_n ) + H(A_2 | A_3 , \ldots , A_n) + H(A_3, \ldots , A_n)\\ | |||
& = \sum_{i = 1}^n H(A_i | A_{i+1} , \ldots , A_n) | |||
\endaligned | |||
</math></center> | |||
(przyjmujemy konwencję <math>H(A|\emptyset)=H(A)</math>) | (przyjmujemy konwencję <math>H(A|\emptyset)=H(A)</math>) | ||
| Linia 137: | Linia 142: | ||
{{fakt|[Warunkowa zasada łańcuchowa]|łańcuch2| | {{fakt|[Warunkowa zasada łańcuchowa]|łańcuch2|Dla dowolnych A, B i C zachodzi | ||
<center><math>H(A,B|C)=H(A|B,C)+H(B|C)</math></center>}} | |||
{{dowod||dw_łańcuch2| | {{dowod||dw_łańcuch2|Dla dowolnego <math>c \in \mathcal{C}</math> rozwijamy | ||
<math>H | <center><math>\aligned | ||
H(A,B| c) & = \sum_{a \in {\mathcal A}, b \in {\mathcal B}} p ( a \wedge b | c) \cdot \log \frac{1}{p( a \wedge b| c )}\\ | |||
& = \sum_{a, b} p (a | b \wedge c) \cdot p(b|c) \cdot \left( \log \frac{1}{p (a | b \wedge c)} + \log \frac{1}{p (b|c) } \right)\\ | |||
& = \sum_{b} p(b|c) \cdot \sum_{a} p (a | b \wedge c) \cdot \log \frac{1}{p (a | b \wedge c)} + \sum_{b} p(b|c) \cdot \log \frac{1}{p (b|c) } \cdot \underbrace{\sum_{a} p (a | b \wedge c)}_{=1} | |||
\endaligned | |||
</math></center> | |||
W powyższym wyliczeniu sumy po a i b obejmują te wartości, dla których odpowiednie prawdopodobieństwa zależne są zdefiniowane (<math>p(x|y)</math> nie jest określone jeśli <math>p(y)=0</math>). | W powyższym wyliczeniu sumy po a i b obejmują te wartości, dla których odpowiednie prawdopodobieństwa zależne są zdefiniowane (<math>p(x|y)</math> nie jest określone jeśli <math>p(y)=0</math>). | ||
Używamy tu łatwego faktu, że jeśli <math>p(a \and b|c)>0</math>, to | Używamy tu łatwego faktu, że jeśli <math>p(a \and b|c)>0</math>, to | ||
<center><math>p ( a \wedge b | c) = \frac{ p(a \wedge b \wedge c)}{p( c)}= \frac{ p(a \wedge b \wedge c)}{ p (b \wedge c)} \cdot \frac{p (b \wedge c)}{p(c)} = p (a | b \wedge c) \cdot p(b|c)</math></center> | |||
Uśredniając po <math>p(c)</math> dostajemy: | |||
<center><math>\aligned | |||
H(A,B|C) & = \sum_{c \in {\mathcal C}} p(c) \cdot H (A,B | c)\\ | |||
& = \sum_{c} p(c) \cdot \sum_{b} p(b|c) \cdot \sum_{a} p (a | b \wedge c) | |||
\cdot \log \frac{1}{p (a | b \wedge c)} + \sum_{c} p(c) \cdot \sum_{b} p(b|c) \cdot \log \frac{1}{p (b|c) }\\ | |||
& = \underbrace{\sum_{b,c} p(b \wedge c) \cdot \sum_{a} p (a | b \wedge c) \cdot \log \frac{1}{p (a | b \wedge c)}}_{=H(A| B,C)} + \underbrace{\sum_{c} p(c) \cdot \sum_{b} p(b|c) \cdot \log \frac{1}{p (b|c) }}_{=H (B | C)} | |||
\endaligned | |||
</math></center>}} | |||
{{definicja|[Informacja warunkowa]|inf_warunkowa| | {{definicja|[Informacja warunkowa]|inf_warunkowa| | ||
Definiujemy '''informację wzajemną A i B warunkowaną przez C''' jako | Definiujemy '''informację wzajemną A i B warunkowaną przez C''' jako | ||
<center><math>\aligned | |||
<math> I(A;B |C) = H(A |C) + H(B|C) - \underbrace{H(A,B|C)}_{=H(A|B,C) + H(B|C)} | I(A;B |C) & = H(A |C) + H(B|C) - \underbrace{H(A,B|C)}_{=H(A|B,C) + H(B|C)} \\ | ||
& = H(A |C) - H(A|B,C) | |||
\endaligned | |||
</math></center> | |||
I wreszcie, '''informację wzajemną A, B i C''' definiujemy jako: | I wreszcie, '''informację wzajemną A, B i C''' definiujemy jako: | ||
<center><math>R(A;B;C)=I(A;B)-I(A;B|C)</math></center>}} | |||
Łatwo sprawdzimy że ta definicja jest rzeczywiście symetryczna, tzn nie zależy od kolejności A, B i C: | Łatwo sprawdzimy że ta definicja jest rzeczywiście symetryczna, tzn nie zależy od kolejności A, B i C: | ||
<center><math>\aligned | |||
I(A;C) - I(A;C|B) = H(A) - H(A|C) - \left( H (A|B) - H(A| B,C) \right) \\ | |||
& = \underbrace{H(A) - H (A|B)}_{=I(A;B)} - \underbrace{ H(A|C) - H(A| B,C)}_{=I(A;B |C)} | |||
\endaligned | |||
</math></center> | |||
<math>I(A; | Należy jednak pamiętać że w przeciwieństwie do <math>I(A;B)</math> i <math>I(A;B|C)</math>, zdefiniowana powyżej <math>R(A;B;C)</math> może mieć '''ujemną''' wartość. | ||
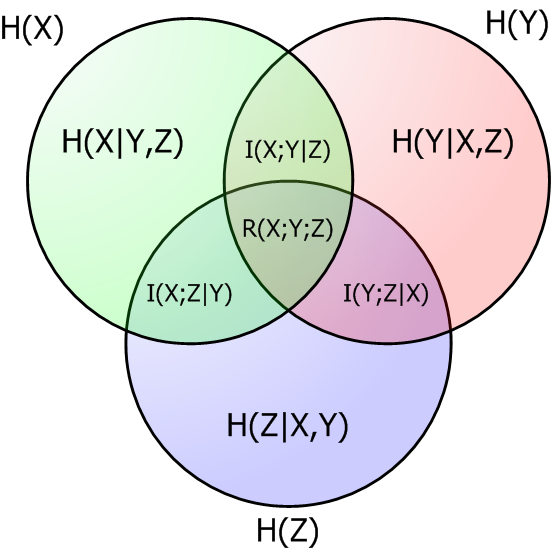
Zależności pomiędzy wartościami H(X), H(Y), H(Z), H(X,Y), H(X,Y|Z), I(X;Y), I(X;Y|Z), R(X;Y;Z) itd. można przedstawić w postaci diagramu: | Zależności pomiędzy wartościami <math>H(X), H(Y), H(Z), H(X,Y), H(X,Y|Z), I(X;Y), I(X;Y|Z), R(X;Y;Z)</math> itd. można przedstawić w postaci diagramu: | ||
[[Grafika:Venn4.png]] | <center>[[Grafika:Venn4.png]]</center> | ||
Wersja z 12:16, 2 sie 2006
Entropia warunkowa i informacja wzajemna
Definicja [Entropia zmiennej losowej]
Jeśli jest zmienną losową, określamy jej entropię jako
Innymi słowy, jest równe wartości oczekiwanej
gdzie p(X) jest zmienną losową na S zdefiniowaną jako
Umowa notacyjna Jeśli zmienne losowe o których mowa będą wynikały z kontekstu, często będziemy omijać zapis i pisać po prostu a. Przykładowo będziemy pisać p(x|y) zamiast , zamiast itp.
Definicja [Entropia warunkowa]
i ogólnie
Zauważmy że jeśli A i B są niezależne, to w powyższej formule a więc . Z drugiej strony . Ogólnie dla dowolnej funkcji mamy
Rzeczywiście, jeśli to , i w konsekwencji .
Entropia łączna
Będziemy również rozważać pary (A,B) jako jedną zmienną losową ,
Prawdopodobieństwo że ta zmienna przyjmie wartość (a,b) wynosi , co zapisujemy w skrócie jako . To prawdopodobieństwo w ogólności jest inne niż . Jeśli dla dowolnych , mówimy że zmienne losowe A i B są niezależne.
Entropia wprost z definicji wynosi
Jeśli A i B są niezależne, to
Z liniowości wartości oczekiwanej dostajemy wtedy
W ogólnym przypadku możemy udowodnić:
Twierdzenie
Dowód
i .
Ważne że powyższe wyrażenie jest dobrze zdefiniowane, bo gdy lub , to również .
Oznaczmy chwilowo
Mamy wtedy
Używając Złotego Lematu dla , dla wszystkich otrzymujemy
Definicja [Informacja]
Komentarz Powyższę definicję łatwo zrozumieć w odniesieniu do Gry w 20 pytań. Przypuścmy że mamy zidentyfikować obiekt który jest parą (a,b) gdzie a i b są wartościami zmiennych losowych A i B. Jeśli A i B są niezależne, najlepsze co możemy zrobić to zidentyfikować niezależnie a i b. Tym samym gramy w dwie niezależne gry „pytania o a” i „pytania o b” (co odpowiada równości ). Jeśli jednak A i B są zależne, możemy wykorzystać tę wzajemną informację do zmniejszenia liczby pytań.
Dla zwiększenia czytelności tekstu, od tej pory będziemy zwykle omijać dolny indeks r, pisząc H, I, itp. Wszędzie tam gdzie nie napisano inaczej, wszystkie twierdzenia odnoszą się do przypadku dowolnego . Bez utraty ogólności czytelnik może założyć r=2.
Komentarz Przekształcając definicję informacji analogicznie jak w ostatnim dowodzie, otrzymujemy:
W takiej postaci widać że informacja jest pewną miarą odległości pomiędzy faktycznym rozkładem zmiennej (A;B), a jej rozkładem gdyby A i B były niezależne.
Warto zauważyć że powyższa suma jest nieujemna, choć niektóre składniki mogą być ujemne.
Istnieje odpowiednik równości , który stosuje się do zmiennych zależnych:
Fakt [Zasada łańcuchowa]
Dowód
Używając zasady łańcuchowej, możemy wyliczać informację na różne sposoby:
Kolejną rzeczą jaką możemy zauważyć to
Łatwo możemy też uogólnić zasadę łańcuchową na przypadek zmiennych
(przyjmujemy konwencję )
Bardziej wyrafinowane uogólnienie możemy uzyskać stosując entropię warunkową:
Fakt [Warunkowa zasada łańcuchowa]
Dowód
W powyższym wyliczeniu sumy po a i b obejmują te wartości, dla których odpowiednie prawdopodobieństwa zależne są zdefiniowane ( nie jest określone jeśli ).
Używamy tu łatwego faktu, że jeśli , to
Uśredniając po dostajemy:
Definicja [Informacja warunkowa]
Definiujemy informację wzajemną A i B warunkowaną przez C jako
I wreszcie, informację wzajemną A, B i C definiujemy jako:
Łatwo sprawdzimy że ta definicja jest rzeczywiście symetryczna, tzn nie zależy od kolejności A, B i C:
Należy jednak pamiętać że w przeciwieństwie do i , zdefiniowana powyżej może mieć ujemną wartość.
Zależności pomiędzy wartościami itd. można przedstawić w postaci diagramu: