Sw3.6-m1-1.2-Slajd13

Systemy wbudowane(9)

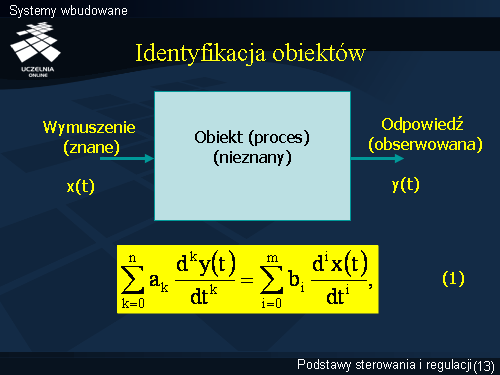
Jak wspomniano, jednym z istotnych problemów sterowania jest identyfikacja właściwości dynamicznych obiektu. Mogą tu zachodzić dwie klasyczne sytuacje. Pierwsza dotyczy przypadku gdy opis dynamiki jest znany na podstawie znajomości zachowania się obiektu wynikającej z wiedzy technologa. Znacznie częściej jednakże mamy do czynienia z sytuacją nieznajomości dynamiki obiektu. Uzyskanie informacji o dynamice obiektu jest możliwe poprzez obserwację jego zachowania na znane pobudzenie (wymuszenie). Teoretycznie można stosować różne znane wymuszenia w celu uzyskania tej wiedzy, jednak w praktyce stosuje się kilka najbardziej charakterystycznych wybranych wymuszeń.

Wróćmy do problemu opisu dynamiki. Ograniczymy się na początek do układów liniowych z jednym wejściem i jednym wyjściem, które opisywane są równaniami liniowymi, w ogólności różniczkowymi, zwyczajnymi (zmienną niezależną jest czas – t), o stałych współczynnikach, wiążących wielkość wejściową x(t) i wyjściową y(t). Równanie dynamiki obiektu przyjmie zatem ogólną postać (1) podaną na rysunku, gdzie:

y(t ) – wielkość wyjściowa,

x(t ) – wielkość wejściowa,

ak , k = 0, 1, 2, ..., n – parametry układu,

bi , i = 0, 1, 2, ..., m – parametry układu,

n – rząd wielkości wyjściowej,

m – rząd wielkości wejściowej.

Rozwiązaniem ogólnym powyższego równania różniczkowego jest funkcja y(t), której postać można wyznaczyć znając funkcję wejściową x(t).

Przyjmując zerowe warunki początkowe, tzn. y(l )(0) = 0 dla l = 0, 1, 2,\ldots, n–1 , można znaleźć funkcję będącą szczegółowym rozwiązaniem równania.

Warunek n ? m jest często nazywany warunkiem realizowalności fizycznej układu (nie istnieje obiekt fizyczny, dla którego powyższy warunek nie jest spełniony).

Powyższy, bardzo naturalny opis dynamiki obiektu (tzw. opis w dziedzinie zmiennej czasu) jest rzadko stosowany, ze względu na trudności z rozwiązywaniem równań różniczkowych, szczególnie w bardziej złożonych przypadkach.

Poszukiwanie rozwiązania równania różniczkowego można uprościć stosując transformację Laplace’a. Ogólnie mówiąc, pozwala ona na przekształcenie równania różniczkowego w równanie algebraiczne. Problem poszukiwania funkcji będącej rozwiązaniem równania różniczkowego zamienia się na problem poszukiwania wartości zmiennych, które są rozwiązaniem równania algebraicznego.

<< Poprzedni slajd | Spis treści | Następny slajd >>