PEE Moduł 9: Różnice pomiędzy wersjami
U_2 |
Nie podano opisu zmian |
||
| Linia 455: | Linia 455: | ||
: <math>T_u(s)=\frac{0,5}{s^2+0,5s+0,5}</math> | : <math>T_u(s)=\frac{0,5}{s^2+0,5s+0,5}</math> | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top"|NOTATKI BEZ SLAJDÓW | |||
''Zadanie 9.2'' | |||
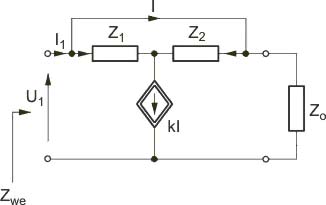
Wyznaczyć impedancję wejściową w postaci operatorowej dla obwodu przedstawionego na rys. poniższym. Impedancję wejściową potraktować jako transmitancję napięciowo-prądową. | |||
{| | |||
|valign="top" width="500px"|[[Grafika:PEE_M9_Rtxt2.jpg]] | |||
|} | |||
Wersja z 06:21, 2 sie 2006

|
Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów |

|
Na slajdzie 9 przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej T(s). |

|
Charakterystyki częstotliwościowe układu n-tego rzędu
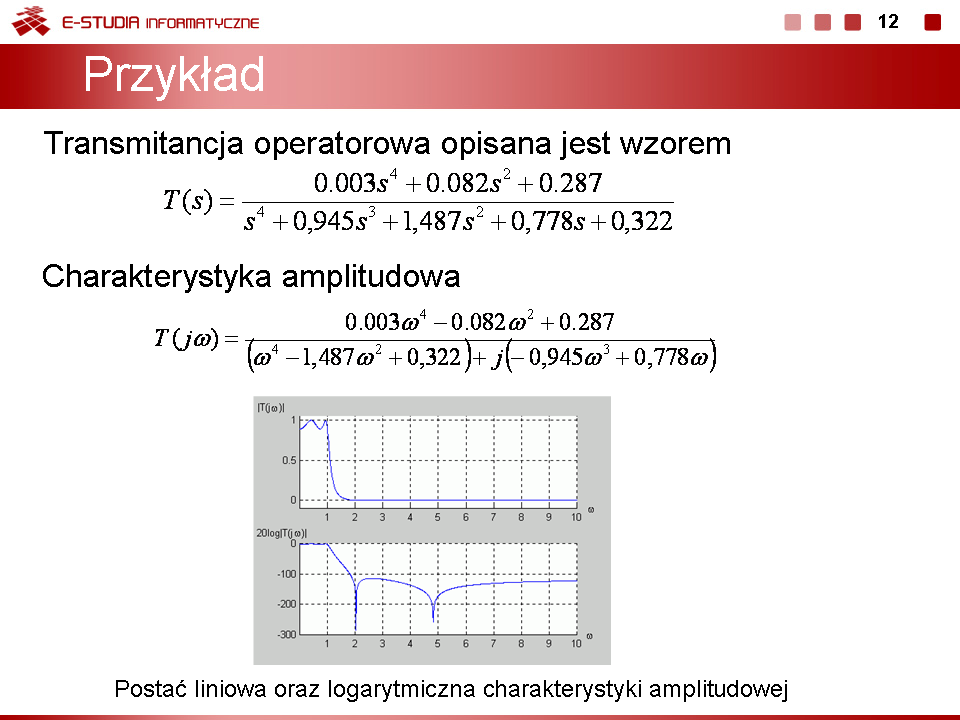
Najbardziej ogólnym przypadkiem jest układ opisany transmitancją operatorową T(s) n-tego rzędu o postaci ogólnej zadanej wzorem
Transmitancja widmowa takiego układu wyznaczana jest z transmitancji operatorowej przez podstawienie . W wyniku otrzymuje się
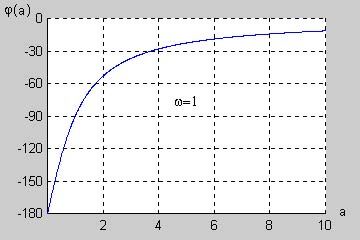
Użytkownik ustala stopień licznika i mianownika transmitancji, a także wartości wszystkich współczynników wielomianu licznika i mianownika. Określa również zakres pulsacji, dla którego wykreślane będą charakterystyki częstotliwościowe. W programie założono, że maksymalny rząd układu nie powinien przekroczyć wartości 9. Wykorzystując podane wcześniej zależności częstotliwościowe program wykreśla charakterystyki amplitudowe (liniową i logarytmiczną wyrażoną w decybelach) oraz charakterystykę fazową w stopniach. Charakterystyki filtru zostają wykreślone w oddzielnych oknach, pozwalających na skalowanie oraz oglądanie w powiększeniu poszczególnych odcinków krzywych. |
|
Zadania sprawdzające
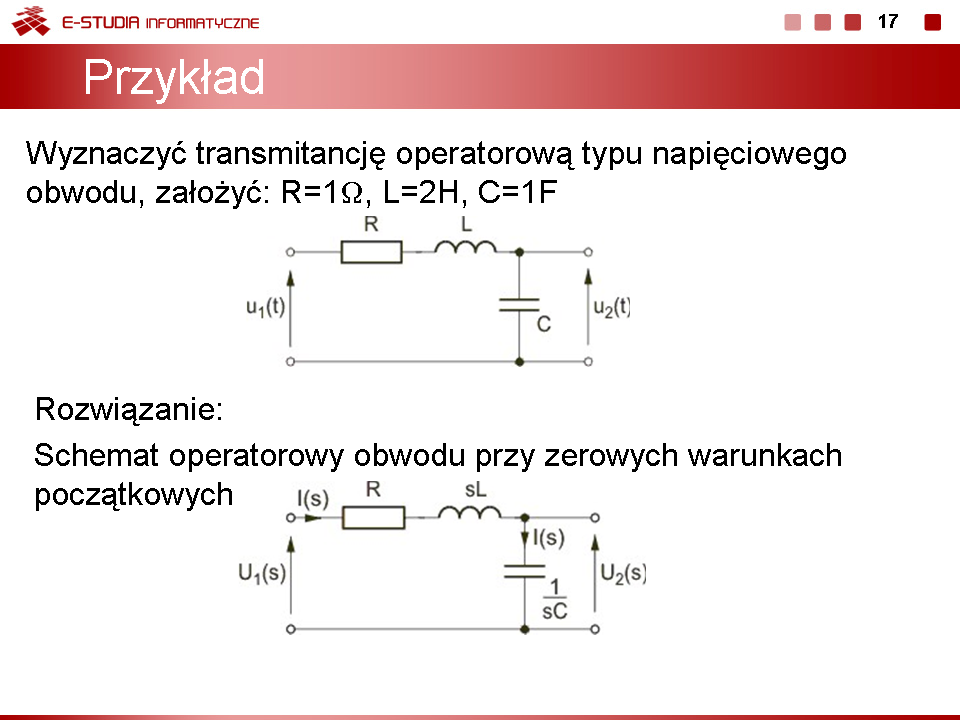
Zadanie 9.1 Wyznaczyć transmitancję operatorową typu napięciowego obwodu z rys. pierwszego na slajdzie 17. Założyć: , , .
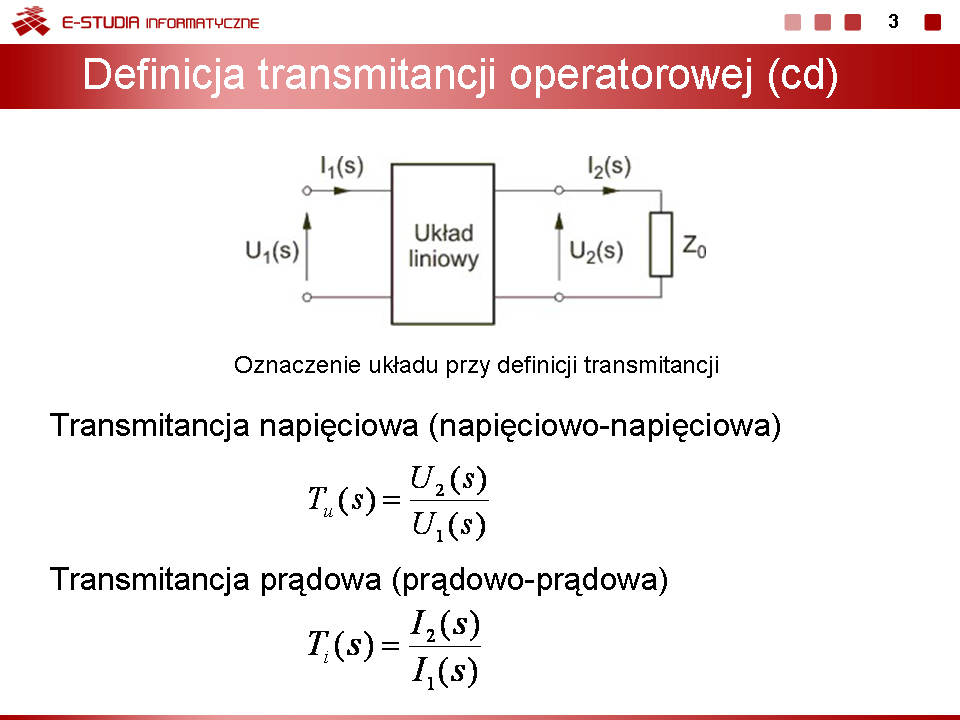
Schemat operatorowy obwodu przy zerowych warunkach początkowych stosowany do wyznaczenia transmitancji przedstawiony jest na rys. drugim na slajdzie 17. Kolejne etapy wyznaczania transmitancji: Prąd I(s)
Napięcie wyjściowe
Transmitancja napięciowa Po podstawieniu wartości liczbowych otrzymuje się |
| NOTATKI BEZ SLAJDÓW
Wyznaczyć impedancję wejściową w postaci operatorowej dla obwodu przedstawionego na rys. poniższym. Impedancję wejściową potraktować jako transmitancję napięciowo-prądową.
|