Analiza matematyczna 1/Ćwiczenia 2: Funkcje elementarne: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „,↵</math>” na „</math>,” |
m Zastępowanie tekstu – „<math> ” na „<math>” |
||
| Linia 24: | Linia 24: | ||
a) Odwrotnością | a) Odwrotnością | ||
funkcji <math>f</math> jest funkcja | funkcji <math>f</math> jest funkcja | ||
<math> x\mapsto \frac{1}{f(x)}=\frac{1}{-x+2}</math>.<br> | <math>x\mapsto \frac{1}{f(x)}=\frac{1}{-x+2}</math>.<br> | ||
b) Wyznaczamy <math>y</math> z równania <math>x=-y+2</math>. Stąd <math>g(x)=-x+2</math> jest | b) Wyznaczamy <math>y</math> z równania <math>x=-y+2</math>. Stąd <math>g(x)=-x+2</math> jest | ||
funkcją odwrotną do <math>f</math>. A więc funkcją odwrotną do <math>f</math> jest | funkcją odwrotną do <math>f</math>. A więc funkcją odwrotną do <math>f</math> jest | ||
| Linia 133: | Linia 133: | ||
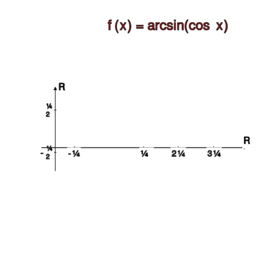
Jeśli <math>0\leq x\leq \pi</math>, to różnica | Jeśli <math>0\leq x\leq \pi</math>, to różnica | ||
<math>\frac{\pi}{2}-x\in \left[-\frac{\pi}{2}, \frac{\pi}{2}\right]</math>. Korzystając ze wzoru | <math>\frac{\pi}{2}-x\in \left[-\frac{\pi}{2}, \frac{\pi}{2}\right]</math>. Korzystając ze wzoru | ||
redukcyjnego: <math> \cos x=\sin\left(\frac{\pi}{2}-x\right)</math>, otrzymujemy | redukcyjnego: <math>\cos x=\sin\left(\frac{\pi}{2}-x\right)</math>, otrzymujemy | ||
<center><math>\arcsin(\cos | <center><math>\arcsin(\cos | ||
x)=\arcsin\left(\sin\left(\frac{\pi}{2}-x\right)\right)=\frac{\pi}{2}-x</math>,</center> | x)=\arcsin\left(\sin\left(\frac{\pi}{2}-x\right)\right)=\frac{\pi}{2}-x</math>,</center> | ||
| Linia 142: | Linia 142: | ||
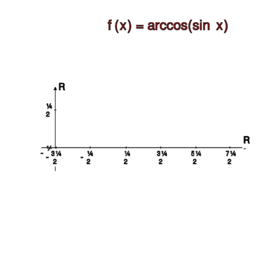
Funkcja <math>x\mapsto \arccos(\sin x)</math> ma okres <math>2\pi</math> i jest określona dla wszystkich liczb rzeczywistych. Podobnie jak w poprzednim przykładzie określimy więc jej wartość w przedziale <math>[-\pi, \pi]</math>. Dzięki okresowości wystarczy to, aby określić jej wartość dla dowolnej liczby rzeczywistej <math>x</math>. Zauważmy, że funkcja <math> y\mapsto f(y)=\arccos y-\frac{\pi}{2}</math> jest nieparzysta, więc <math>f(-y)=-f(y)</math>, stąd | Funkcja <math>x\mapsto \arccos(\sin x)</math> ma okres <math>2\pi</math> i jest określona dla wszystkich liczb rzeczywistych. Podobnie jak w poprzednim przykładzie określimy więc jej wartość w przedziale <math>[-\pi, \pi]</math>. Dzięki okresowości wystarczy to, aby określić jej wartość dla dowolnej liczby rzeczywistej <math>x</math>. Zauważmy, że funkcja <math>y\mapsto f(y)=\arccos y-\frac{\pi}{2}</math> jest nieparzysta, więc <math>f(-y)=-f(y)</math>, stąd | ||
<center> | <center> | ||
| Linia 157: | Linia 157: | ||
</center> | </center> | ||
dla <math> x\in \bigg[0, \frac{\pi}{2}\bigg]</math>. Natomiast dla | dla <math>x\in \bigg[0, \frac{\pi}{2}\bigg]</math>. Natomiast dla | ||
<math> x\in \bigg[\frac{\pi}{2},\pi\bigg]</math> mamy równość | <math>x\in \bigg[\frac{\pi}{2},\pi\bigg]</math> mamy równość | ||
<center> | <center> | ||
| Linia 165: | Linia 165: | ||
Stąd dla | Stąd dla | ||
<math> \bigg|x-\frac{\pi}{2}\bigg|\leq \frac{\pi}{2}</math> mamy | <math>\bigg|x-\frac{\pi}{2}\bigg|\leq \frac{\pi}{2}</math> mamy | ||
<center> | <center> | ||
| Linia 173: | Linia 173: | ||
Korzystając teraz z nieparzystości | Korzystając teraz z nieparzystości | ||
funkcji | funkcji | ||
<math> y\mapsto \arccos y-\frac{\pi}{2}</math> dla <math>x\in [-\pi, 0]</math>, | <math>y\mapsto \arccos y-\frac{\pi}{2}</math> dla <math>x\in [-\pi, 0]</math>, | ||
otrzymamy <math>\arccos(\sin x)=\pi-\bigg|x+\frac{\pi}{2}\bigg|</math>. Stąd | otrzymamy <math>\arccos(\sin x)=\pi-\bigg|x+\frac{\pi}{2}\bigg|</math>. Stąd | ||
ostatecznie dla <math>x\in[-\pi, \pi]</math> mamy | ostatecznie dla <math>x\in[-\pi, \pi]</math> mamy | ||
Wersja z 22:18, 11 wrz 2023
Funkcje elementarne
Ćwiczenie 2.1.
Dana jest funkcja afiniczna . Wyznaczyć:
a) odwrotność tej funkcji,
b) funkcję odwrotną do ,
c) złożenie , , , .
d) Czy istnieje malejąca funkcja
afiniczna taka, że ?
Ćwiczenie 2.2.
Dana jest homografia
. Wyznaczyć:
a) odwrotność tej homografii,
b) homografię odwrotną,
c) złożenie , , oraz .
d) Czy istnieje homografia taka, że
?
Ćwiczenie 2.3.
Wyrazić w prostszej postaci:
a) , ,
b) , ,
c) , ,
d) , ,
e) , .
Ćwiczenie 2.4.
Wykazać, że dla dowolnych liczb ,
zachodzą równości:
a) ,
b) .
Ćwiczenie 2.5.
a) Niech dla ... Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla ...
Ćwiczenie 2.6.
a) Niech dla ... Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla ...
c) Wykazać, że dla dowolnej liczby .. istnieje
wielomian taki, że oraz są restrykcjami -
odpowiednio do przedziałów oraz -
wielomianu .