PEE Moduł 9: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 256: | Linia 256: | ||
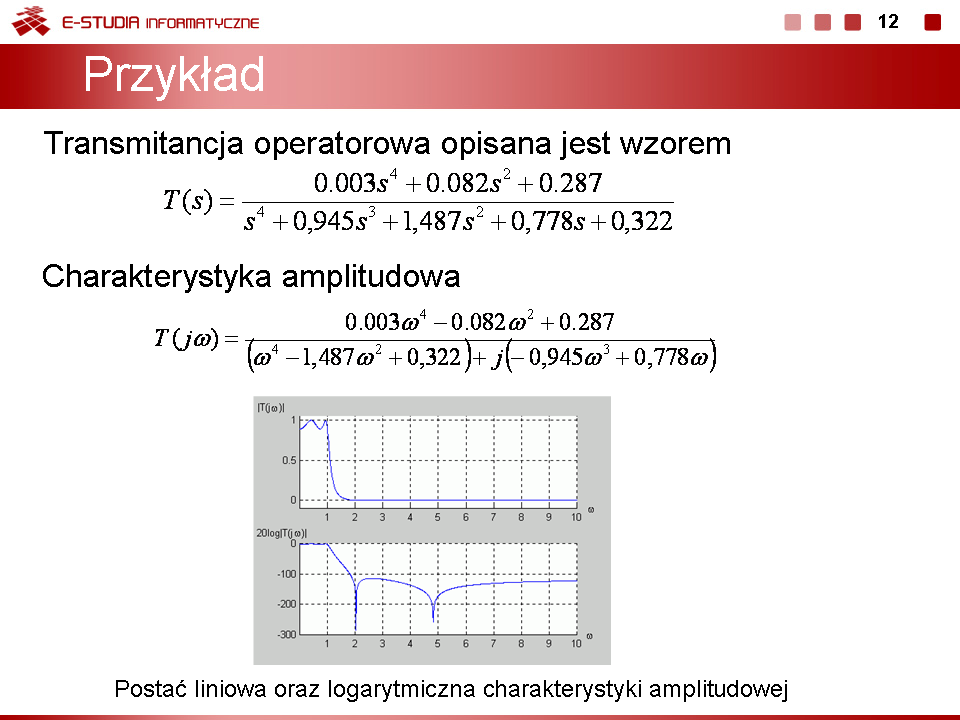
Charakterystyki częstotliwościowe przedstawia się zwykle na wykresie modułu lub fazy w zależności od pulsacji (częstotliwości). Jeśli wielkości podlegające wykreślaniu różnią się znacznie pod względem wartości (np. zmieniają się w zakresie od <math>1\,</math> do <math>10^6</math>) wygodnie jest wprowadzić skalę logarytmiczną zwykle o podstawie 10. Dotyczy to określonego zakresu częstotliwości. W przypadku charakterystyki amplitudowej skalę logarytmiczną przelicza się na decybele (dB) definiując '''logarytmiczną charakterystykę amplitudową''' | Charakterystyki częstotliwościowe przedstawia się zwykle na wykresie modułu lub fazy w zależności od pulsacji (częstotliwości). Jeśli wielkości podlegające wykreślaniu różnią się znacznie pod względem wartości (np. zmieniają się w zakresie od <math>1\,</math> do <math>10^6</math>) wygodnie jest wprowadzić skalę logarytmiczną zwykle o podstawie 10. Dotyczy to określonego zakresu częstotliwości. W przypadku charakterystyki amplitudowej skalę logarytmiczną przelicza się na decybele (dB) definiując '''logarytmiczną charakterystykę amplitudową''' | ||
: <math>20log_{10}(|T(j\omega)|)</math> | : <math>20log_{10}(|T(j\omega)|)</math> | ||
| Linia 344: | Linia 343: | ||
Charakterystyka amplitudowa jest typu hiperbolicznego, a charakterystyka fazowa stała (przesunięcie fazowe stałe i równe <math>-90^\circ</math> niezależnie od częstotliwości). | Charakterystyka amplitudowa jest typu hiperbolicznego, a charakterystyka fazowa stała (przesunięcie fazowe stałe i równe <math>-90^\circ</math> niezależnie od częstotliwości). | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd15.png]] | |||
|valign="top"|'''Przesuwnik fazowy''' | |||
Przesuwnik fazowy jest układem przesuwającym fazę napięcia wyjściowego względem wejściowego bez zmiany amplitudy sygnału. Transmitancję przesuwnika fazowego określa zależność | |||
: <math>T(s)=\frac{-s+a}{s+a}</math> | |||
Charakterystyka częstotliwościowa przesuwnika określona jest następującą relacją | |||
<math>T(j\omega)=\frac{-j\omega+a}{j\omega+a}=\frac{\sqrt{\omega^2+a^2}}{\sqrt{\omega^2+a^2}}\cdot \frac{e^{-j\phi(\omega)}}{e^{j\phi(\omega)}}=</math> | |||
: <math>=1e^{-j2\phi(\omega)}</math> | |||
gdzie kąt <math>\phi(\omega)</math> określony jest wzorem <math>\phi(\omega)=arctg(\frac{\omega}{a})</math>. Powyższa zależność potwierdza, że przesuwnik fazowy nie zmienia amplitudy sygnału wejściowego <math>(|T(j\omega)|=1)</math> a wpływa jedynie na przesunięcie fazowe między sygnałem wejściowym i wyjściowym. | |||
Charakterystyka fazowa przesuwnika określona jest zależnością | |||
: <math>\varphi(\omega)=-2arctg(\frac{\omega}{a})</math> | |||
Na slajdzie 15 przedstawiono wykres charakterystyki fazowej przesuwnika o transmitancji ze slajdu 6 w funkcji pulsacji dla wartości a=1. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 23:06, 1 sie 2006

|
Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów |

|
Na slajdzie 9 przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej T(s). |