Analiza matematyczna 2/Ćwiczenia 12: Całka krzwoliniowa. Twierdzenie Greena: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „.↵</math>” na „</math>” |
m Zastępowanie tekstu – „,↵</math>” na „</math>,” |
||
| Linia 5: | Linia 5: | ||
Policzyć | Policzyć | ||
<center><math>\int\limits_C ydx+2x dy | <center><math>\int\limits_C ydx+2x dy</math>,</center> | ||
</math></center> | |||
gdzie <math>C</math> jest łukiem cykloidy danej | gdzie <math>C</math> jest łukiem cykloidy danej | ||
| Linia 49: | Linia 48: | ||
<center> | <center> | ||
<math>\int\limits_K (x+y)dx+y^2 dy | <math>\int\limits_K (x+y)dx+y^2 dy</math>, | ||
</math> | |||
</center> | </center> | ||
| Linia 185: | Linia 183: | ||
y} | y} | ||
= | = | ||
3x^2+4xy | 3x^2+4xy</math>,</center> | ||
</math></center> | |||
a zatem całka nie zależy od drogi całkowania. | a zatem całka nie zależy od drogi całkowania. | ||
| Linia 248: | Linia 245: | ||
<center><math>\int \big(3x^2y+2xy^2+1\big)dx | <center><math>\int \big(3x^2y+2xy^2+1\big)dx | ||
= | = | ||
\int \frac{\partial \varrho}{\partial x}(x,y)dx | \int \frac{\partial \varrho}{\partial x}(x,y)dx</math>,</center> | ||
</math></center> | |||
dostaniemy | dostaniemy | ||
| Linia 255: | Linia 251: | ||
<center><math>\varrho(x,y) | <center><math>\varrho(x,y) | ||
= | = | ||
x^3y+x^2y^2+x+g(y) | x^3y+x^2y^2+x+g(y)</math>,</center> | ||
</math></center> | |||
gdzie <math>g</math> jest pewną | gdzie <math>g</math> jest pewną | ||
| Linia 267: | Linia 262: | ||
\frac{\partial(x^3y+x^2y^2+y+g(y))}{\partial y} | \frac{\partial(x^3y+x^2y^2+y+g(y))}{\partial y} | ||
= | = | ||
x^3+2x^2y+1+g'(y) | x^3+2x^2y+1+g'(y)</math>,</center> | ||
</math></center> | |||
a skoro mamy mieć | a skoro mamy mieć | ||
| Linia 274: | Linia 268: | ||
<center><math>x^3+2x^2y+1 | <center><math>x^3+2x^2y+1 | ||
= | = | ||
\frac{\partial \varrho}{\partial y}(x,y) | \frac{\partial \varrho}{\partial y}(x,y)</math>,</center> | ||
</math></center> | |||
to musi być | to musi być | ||
| Linia 281: | Linia 274: | ||
<center><math>g'(y) | <center><math>g'(y) | ||
= | = | ||
0 | 0</math>,</center> | ||
</math></center> | |||
czyli | czyli | ||
| Linia 306: | Linia 298: | ||
4 | 4 | ||
= | = | ||
\varrho(1,1)-\varrho(0,0) | \varrho(1,1)-\varrho(0,0)</math>,</center> | ||
</math></center> | |||
co obrazuje ogólne twierdzenie, że dla pola potencjalnego całka | co obrazuje ogólne twierdzenie, że dla pola potencjalnego całka | ||
| Linia 318: | Linia 309: | ||
Korzystając z twierdzenia Greena, policzyć | Korzystając z twierdzenia Greena, policzyć | ||
<center><math>\int\limits_K -yx^2dx+xy^2dy | <center><math>\int\limits_K -yx^2dx+xy^2dy</math>,</center> | ||
</math></center> | |||
gdzie <math>K</math> jest okręgiem | gdzie <math>K</math> jest okręgiem | ||
| Linia 352: | Linia 342: | ||
Policzyć całkę | Policzyć całkę | ||
<center><math>\int\limits_K(e^x+e^y-y )dx+(xe^y)dy | <center><math>\int\limits_K(e^x+e^y-y )dx+(xe^y)dy</math>,</center> | ||
</math></center> | |||
gdzie <math>K</math> jest wykresem funkcji | gdzie <math>K</math> jest wykresem funkcji | ||
| Linia 456: | Linia 445: | ||
Policzyć całkę krzywoliniową: | Policzyć całkę krzywoliniową: | ||
<center><math>\int\limits_K (e^{x}\sin y)dx+(e^{x}\cos y)dy | <center><math>\int\limits_K (e^{x}\sin y)dx+(e^{x}\cos y)dy</math>,</center> | ||
</math></center> | |||
gdzie <math>K</math> jest parabolą | gdzie <math>K</math> jest parabolą | ||
| Linia 529: | Linia 517: | ||
<math>\frac{x^2}{a^2}+\frac{y^2}{b^2} | <math>\frac{x^2}{a^2}+\frac{y^2}{b^2} | ||
= | = | ||
1 | 1</math>, | ||
</math> | |||
</center> | </center> | ||
| Linia 585: | Linia 572: | ||
<math>x^{\frac{2}{3}}+y^{\frac{2}{3}} | <math>x^{\frac{2}{3}}+y^{\frac{2}{3}} | ||
= | = | ||
a^{\frac{2}{3}} | a^{\frac{2}{3}}</math>, | ||
</math> | |||
</center> | </center> | ||
Aktualna wersja na dzień 21:43, 11 wrz 2023
Całka krzywoliniowa. Twierdzenie Greena
Ćwiczenie 12.1.
Policzyć
gdzie jest łukiem cykloidy danej parametrycznie:
Ćwiczenie 12.2.
Policzyć
,
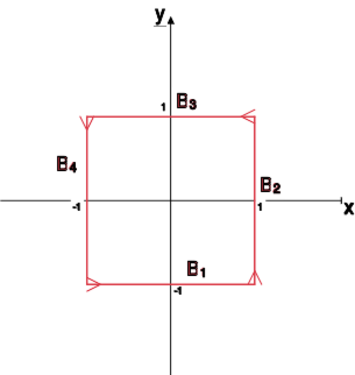
gdzie jest kwadratem o wierzchołkach w obieganym przeciwnie do ruchu wskazówek zegara.
Ćwiczenie 12.3.
W pewnym polu sił składowe pola wynoszą
Policzyć pracę potrzebną do przesunięcia punktu materialnego wzdłuż krzywej łączącej punkt z punktem , danej wzorem .
Ćwiczenie 12.4.
Znaleźć (lub odgadnąć) potencjał dla pola sił z ćwiczenia 12.3.
Ćwiczenie 12.5.
Korzystając z twierdzenia Greena, policzyć
gdzie jest okręgiem środku w i promieniu .
Ćwiczenie 12.6.
Policzyć całkę
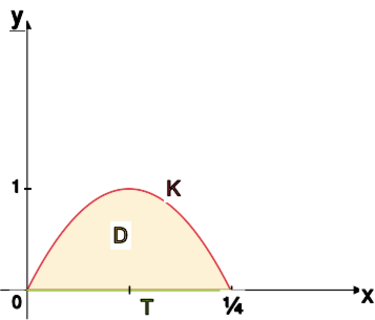
gdzie jest wykresem funkcji , dla .
Ćwiczenie 12.7.
Policzyć całkę krzywoliniową:
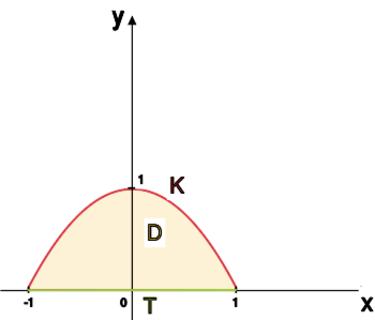
gdzie jest parabolą pomiędzy punktami a .
Ćwiczenie 12.8.
Za pomocą całki krzywoliniowej skierowanej obliczyć pole ograniczone elipsą
,
gdzie są dane.
Ćwiczenie 12.9.
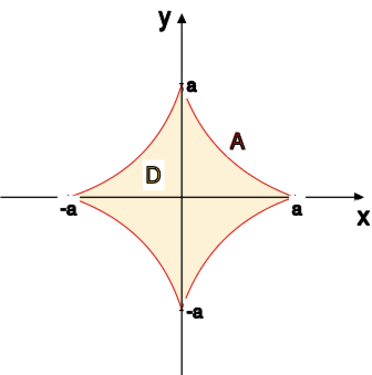
Za pomocą całki krzywoliniowej skierowanej obliczyć pole ograniczone asteroidą
,
gdzie jest dane.