Analiza matematyczna 1/Ćwiczenia 2: Funkcje elementarne: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „.</math>” na „</math>.” |
m Zastępowanie tekstu – „.↵</math>” na „</math>” |
||
| Linia 36: | Linia 36: | ||
= | = | ||
\left\{ \begin{array}{ll} f, &\text{ jeśli }n \text{ jest liczbą nieparzystą},\\ | \left\{ \begin{array}{ll} f, &\text{ jeśli }n \text{ jest liczbą nieparzystą},\\ | ||
\mathrm{id}\, &\text{ jeśli }n \text{ jest liczbą parzystą},\end{array}\right | \mathrm{id}\, &\text{ jeśli }n \text{ jest liczbą parzystą},\end{array}\right</math></center> | ||
</math></center> | |||
wobec tego <math>f^9=f</math>.<br> | wobec tego <math>f^9=f</math>.<br> | ||
| Linia 87: | Linia 86: | ||
= | = | ||
\left\{ \begin{array}{ll} f, &\text{ jeśli }n \text{ jest liczbą nieparzystą},\\ | \left\{ \begin{array}{ll} f, &\text{ jeśli }n \text{ jest liczbą nieparzystą},\\ | ||
\mathrm{id}\, &\text{ jeśli }n \text{jest liczbą parzystą,}\end{array}\right | \mathrm{id}\, &\text{ jeśli }n \text{jest liczbą parzystą,}\end{array}\right</math></center> | ||
</math></center> | |||
wobec tego <math>f^3=f</math>, <math>f^{11}=f</math>.<br> | wobec tego <math>f^3=f</math>, <math>f^{11}=f</math>.<br> | ||
| Linia 148: | Linia 146: | ||
<center> | <center> | ||
<math>\arccos (-y)=\pi -\arccos y</math> dla <math> | <math>\arccos (-y)=\pi -\arccos y</math> dla <math> | ||
|y|\leq\frac{\pi}{2} | |y|\leq\frac{\pi}{2}</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 165: | Linia 162: | ||
<center> | <center> | ||
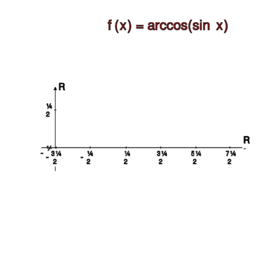
<math>\arccos (\sin x) =-\bigg(\frac{\pi}{2}-x\bigg) =x-\frac{\pi}{2} | <math>\arccos (\sin x) =-\bigg(\frac{\pi}{2}-x\bigg) =x-\frac{\pi}{2}</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 173: | Linia 169: | ||
<center> | <center> | ||
<math>\arccos (\sin x)) =\bigg|x-\frac{\pi}{2}\bigg| | <math>\arccos (\sin x)) =\bigg|x-\frac{\pi}{2}\bigg|</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 187: | Linia 182: | ||
&\frac{\pi}{2}-x, &\text{ dla } & -\frac{\pi}{2} \leq x\leq \frac{\pi}{2}\\ | &\frac{\pi}{2}-x, &\text{ dla } & -\frac{\pi}{2} \leq x\leq \frac{\pi}{2}\\ | ||
&x-\frac{\pi}{2}, &\text{ dla } & +\frac{\pi}{2} \leq x\leq \pi.\end{align} | &x-\frac{\pi}{2}, &\text{ dla } & +\frac{\pi}{2} \leq x\leq \pi.\end{align} | ||
\right | \right</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 205: | Linia 199: | ||
Podobnie <math>x\mapsto \mathrm{arc\,ctg}\,(\mathrm{tg}\, x)</math> jest nieparzysta, okresowa o okresie <math>\pi</math>. Wystarczy więc rozważyć ją np. w przedziale <math>\bigg(-\frac{\pi}{2},\frac{\pi}{2}\bigg)</math>, gdzie zachodzi równość: | Podobnie <math>x\mapsto \mathrm{arc\,ctg}\,(\mathrm{tg}\, x)</math> jest nieparzysta, okresowa o okresie <math>\pi</math>. Wystarczy więc rozważyć ją np. w przedziale <math>\bigg(-\frac{\pi}{2},\frac{\pi}{2}\bigg)</math>, gdzie zachodzi równość: | ||
<center><math>\mathrm{arc\,ctg}\,(\mathrm{tg}\, x)=\mathrm{arc\,ctg}\,(\mathrm{ctg}\,(\frac{\pi}{2}-x))=\frac{\pi}{2}-x | <center><math>\mathrm{arc\,ctg}\,(\mathrm{tg}\, x)=\mathrm{arc\,ctg}\,(\mathrm{ctg}\,(\frac{\pi}{2}-x))=\frac{\pi}{2}-x</math></center> | ||
</math></center> | |||
d) Pamiętając, że <math>\mathrm{tg}\, u=\frac{1}{\mathrm{ctg}\, u}</math>, otrzymamy | d) Pamiętając, że <math>\mathrm{tg}\, u=\frac{1}{\mathrm{ctg}\, u}</math>, otrzymamy | ||
Wersja z 21:32, 11 wrz 2023
Funkcje elementarne
Ćwiczenie 2.1.
Dana jest funkcja afiniczna . Wyznaczyć:
a) odwrotność tej funkcji,
b) funkcję odwrotną do ,
c) złożenie , , , .
d) Czy istnieje malejąca funkcja
afiniczna taka, że ?
Ćwiczenie 2.2.
Dana jest homografia
. Wyznaczyć:
a) odwrotność tej homografii,
b) homografię odwrotną,
c) złożenie , , oraz .
d) Czy istnieje homografia taka, że
?
Ćwiczenie 2.3.
Wyrazić w prostszej postaci:
a) , ,
b) , ,
c) , ,
d) , ,
e) , .
Ćwiczenie 2.4.
Wykazać, że dla dowolnych liczb ,
zachodzą równości:
a) ,
b) .
Ćwiczenie 2.5.
a) Niech dla ... Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla ...
Ćwiczenie 2.6.
a) Niech dla ... Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla ...
c) Wykazać, że dla dowolnej liczby .. istnieje
wielomian taki, że oraz są restrykcjami -
odpowiednio do przedziałów oraz -
wielomianu .