Analiza matematyczna 1/Ćwiczenia 2: Funkcje elementarne

Funkcje elementarne

Ćwiczenie 2.1.

Dana jest funkcja afiniczna $f(x)=-x+2$. Wyznaczyć:
a) odwrotność tej funkcji,
b) funkcję odwrotną do $f$,
c) złożenie $f^2=f\circ f$, $f^3=f\circ f\circ f$, $f^4=f\circ f\circ f\circ f$, $f^9=f\circ f\circ f\circ f\circ f\circ f\circ f\circ f\circ f$.
d) Czy istnieje malejąca funkcja afiniczna $g$ taka, że $(g\circ g)(x)=4x+3$?

Wskazówka

a) Co to jest odwrotność?
b) Wystarczy wyznaczyć $y$ z równania $x=f(y)$.
c) Skorzystać z definicji złożenia. Składanie funkcji jest łączne.
d) Niech $g(x)=ax+b$. Jakie warunki muszą spełniać współczynniki $a$ i $b$, aby $(g\circ g)(x)=4x+3$?

Rozwiązanie

a) Odwrotnością funkcji $f$ jest funkcja $x\mapsto \frac{1}{f(x)}=\frac{1}{-x+2}$.
b) Wyznaczamy $y$ z równania $x=-y+2$. Stąd $g(x)=-x+2$ jest funkcją odwrotną do $f$. A więc funkcją odwrotną do $f$ jest $f$.
c) Funkcją odwrotną do $f$ jest $f$, więc $f\circ f=\mathrm{i}\mathrm{d}$,, gdzie $\mathrm{i}\mathrm{d}:x\mapsto x$ oznacza odwzorowanie identycznościowe. Wobec tego $f^3=(f\circ f)\circ f=\mathrm{i}\mathrm{d}\circ f=f$. Podobnie $f^4=(f\circ f)\circ (f\circ f)=\mathrm{i}\mathrm{d}\circ \mathrm{i}\mathrm{d}=\mathrm{i}\mathrm{d}$,. Spostrzegamy, że:

$f^n=\{\begin{array}{ll}f,& \text{ jeśli }n\text{ jest liczbą nieparzystą},\\ \mathrm{i}\mathrm{d}& \text{ jeśli }n\text{ jest liczbą parzystą},\end{array}$

wobec tego $f^9=f$.
d) Jeśli $g(x)=ax+b$, to $(g\circ g)(x)=a(ax+b)+b=a^{2}x+ab+b$. Jeśli $(g\circ g)(x)=4x+3$, to współczynniki $a$, $b$ muszą spełniać układ równań:

Parser nie mógł rozpoznać (błąd składni): {\displaystyle \left\{\begin{array}{l} a^2=4\\ (a+1)b=3 \end{array}\right} .

który spełniają dwie pary liczb $(a,b)\in \{(-2,-3),(2,1)\}$. Funkcja $g_1(x)=-2x-3$ jest malejąca, a $g_2(x)=2x+1$ jest rosnącą funkcją afiniczną.

Ćwiczenie 2.2.

Dana jest homografia $f(x)=\frac{x+1}{x-1}$. Wyznaczyć:
a) odwrotność tej homografii,
b) homografię odwrotną,
c) złożenie $f^2=f\circ f$, $f^3=f\circ f\circ f$, $f^4=f\circ f\circ f\circ f$ oraz $f^{11}=f\circ f\circ f\circ f\circ f\circ f\circ f\circ f\circ f\circ f\circ f$.
d) Czy istnieje homografia $g:\mathbb{ℝ}\mapsto \mathbb{ℝ}$ taka, że $g\circ g=f$?

Wskazówka

a), b) c) Zastosować wskazówki do ćwiczenia 2.1.
d) Niech $g(x)=\frac{ax+b}{cx+d}$. Zauważyć, że można przyjąć, że $c=1$ (dlaczego?). Jakie równania muszą spełniać współczynniki $a,b,d$, aby $g\circ g=f$?

Rozwiązanie

a) Odwrotnością danej homografii jest $x\mapsto \frac{1}{f(x)}=\frac{x-1}{x+1}$.
b) Homografię odwrotną do $f$ otrzymamy, wyznaczając $x$ z równania $y=\frac{x+1}{x-1}$. Stąd $x=\frac{y+1}{y-1}$, czyli homografią odwrotną do $f$ jest ta sama funkcja.
c) Skoro $f^{-1}=f$, więc - podobnie jak w ćwiczeniu 2.1. - złożenie $f\circ f=\mathrm{i}\mathrm{d}$,, $f^4=(f\circ f)\circ (f\circ f)=\mathrm{i}\mathrm{d}\circ \mathrm{i}\mathrm{d}=\mathrm{i}\mathrm{d}$,. Spostrzegamy, że:

$f^n=\{\begin{array}{ll}f,& \text{ jeśli }n\text{ jest liczbą nieparzystą},\\ \mathrm{i}\mathrm{d}& \text{ jeśli }n\text{jest liczbą parzystą,}\end{array}$

wobec tego $f^3=f$, $f^{11}=f$.
d) Niech $g(x)=\frac{ax+b}{cx+d}$. Współczynnik $c\ne 0$, gdyż w przeciwnym przypadku funkcja $g$ byłaby afiniczna i złożenie $g\circ g$ byłoby funkcją afiniczną, co nie jest możliwe. Skoro $c\ne 0$ możemy podzielić licznik i mianownik rozważanego ułamka przez stałą $c$ i przyjąć, że $c=1$ to znaczy: $g(x)=\frac{ax+b}{x+d}$. Wobec tego

$\begin{array}{rl}(g\circ g)(x)=& g(g(x))=\frac{ag(x)+b}{g(x)+d}\\ =& \frac{a\frac{ax+b}{x+d}+b}{\frac{ax+b}{x+d}+d}=\frac{a(ax+b)+b(x+d)}{ax+b+d(x+d)}=\frac{(a^2+b)x+(ab+bd)}{(a+d)x+(b+d^2)}.\end{array}$

Równość $g\circ g=f$ zachodziłaby, gdyby odpowiednie współczynniki homografii $g\circ g$ oraz $f$ były równe,

$0\ne a^2+b=b(a+d)=a+d=-(b+d^2)$.

Ale jest to niemożliwe, gdyż z równości $b(a+d)=a+d$ wynika, że $b=1$, co pociąga za sobą w konsekwencji nierówność: $1\le a^2+1=a^2+b=-(b+d^2)=-(1+d^2)\le -1$, która jest fałszywa. Nie ma więc takiej homografii $g:\mathbb{ℝ}\mapsto \mathbb{ℝ}$, aby $g\circ g=f$.

Ćwiczenie 2.3.

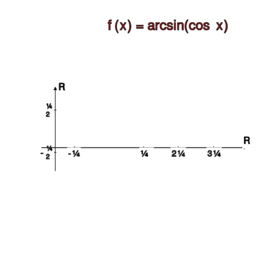
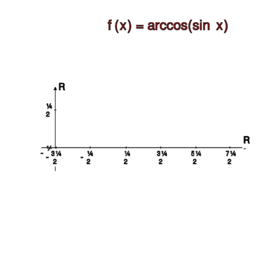
Wyrazić w prostszej postaci:
a) $\arcsin (\cos x)$, $\arccos (\sin x)$,
b) $\sin (\arccos x)$, $\cos (\arcsin x)$,
c) $\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}(\mathrm{c}\mathrm{t}\mathrm{g}x)$, $\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{t}\mathrm{g}(\mathrm{t}\mathrm{g}x)$,
d) $\mathrm{t}\mathrm{g}(\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{t}\mathrm{g}x)$, $\mathrm{c}\mathrm{t}\mathrm{g}(\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}x)$,
e) $\sinh (\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)$, $\cosh (\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}x)$.

Wskazówka

a) Skorzystać ze związku: $\arccos x=\arcsin (-x)+\frac{\pi }{2}$.
b) Skorzystać z jedynki trygonometrycznej.

Rozwiązanie

a) Zauważmy, że funkcja $x\mapsto \arcsin (\cos x)$ jest określona w każdym punkcie zbioru liczb rzeczywistych i jest okresowa o okresie $2\pi$. Wystarczy więc wyznaczyć jej wartości w jakimkolwiek przedziale postaci $[a-\pi ,a+\pi ]$. Funkcja cosinus jest parzysta, stąd złożenie $x\mapsto \arcsin (\cos x)$ jest funkcją parzystą. Wystarczy więc rozważyć wyrażenie $\arcsin (\cos x)$ w zbiorze $0\le x\le \pi$. Jeśli $0\le x\le \pi$, to różnica $\frac{\pi }{2}-x\in [-\frac{\pi }{2},\frac{\pi }{2}]$. Korzystając ze wzoru redukcyjnego: $\cos x=\sin (\frac{\pi }{2}-x)$, otrzymujemy

$\arcsin (\cos x)=\arcsin (\sin (\frac{\pi }{2}-x))=\frac{\pi }{2}-x$, dla $0\le x\le \pi$. Wobec parzystości rozważanej funkcji mamy dla $-\pi \le x\le \pi$ równość $\arcsin (\cos x)=\frac{\pi }{2}-|x|$.

Rysunek do ćwiczenia 2.3.(a)

Rysunek do ćwiczenia 2.3.(a)

Funkcja $x\mapsto \arccos (\sin x)$ ma okres $2\pi$ i jest określona dla wszystkich liczb rzeczywistych. Podobnie jak w poprzednim przykładzie określimy więc jej wartość w przedziale $[-\pi ,\pi ]$. Dzięki okresowości wystarczy to, aby określić jej wartość dla dowolnej liczby rzeczywistej $x$. Zauważmy, że funkcja $y\mapsto f(y)=\arccos y-\frac{\pi }{2}$ jest nieparzysta, więc $f(-y)=-f(y)$, stąd

$\arccos (-y)=\pi -\arccos y$ dla $|y|\le \frac{\pi }{2}.$

Rozumując jak poprzednio, na mocy wzoru redukcyjnego równość: $\sin x=\cos (\frac{\pi }{2}-x)$. Stąd

$\arccos (\sin x))=\arccos (\cos (\frac{\pi }{2}-x))=\frac{\pi }{2}-x,$

dla $x\in [0,\frac{\pi }{2}]$. Natomiast dla $x\in [\frac{\pi }{2},\pi ]$ mamy równość

$\arccos (\sin x)=-(\frac{\pi }{2}-x)=x-\frac{\pi }{2}.$

Stąd dla $|x-\frac{\pi }{2}|\le \frac{\pi }{2}$ mamy

$\arccos (\sin x))=|x-\frac{\pi }{2}|.$

Korzystając teraz z nieparzystości funkcji $y\mapsto \arccos y-\frac{\pi }{2}$ dla $x\in [-\pi ,0]$, otrzymamy $\arccos (\sin x)=\pi -|x+\frac{\pi }{2}|$. Stąd ostatecznie dla $x\in [-\pi ,\pi ]$ mamy

$\arccos (\sin x)=\{\begin{array}{rlrl}& \frac{3\pi }{2}+x,& \text{ dla }& -\pi \le x\le -\frac{\pi }{2}\\ & \frac{\pi }{2}-x,& \text{ dla }& -\frac{\pi }{2}\le x\le \frac{\pi }{2}\\ & x-\frac{\pi }{2},& \text{ dla }& +\frac{\pi }{2}\le x\le \pi .\end{array}$

b) Niech $y=\arccos x$. Zatem $\sin y\ge 0$. Z jedynki trygonometrycznej: ${\sin }^{2}y=1-{\cos }^{2}y=1-x^2$. Stąd $\sin (\arccos x)=\sqrt{1-x^2}$ dla $-1\le x\le 1$.

Podobnie dostajemy równość: $\cos (\arcsin x)=\sqrt{1-x^2}$ dla $-1\le x\le 1$.
c) Funkcja $x\mapsto \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}(\mathrm{c}\mathrm{t}\mathrm{g}x)$ jest nieparzysta, gdyż jest złożeniem dwóch funkcji nieparzystych: $x\mapsto \mathrm{c}\mathrm{t}\mathrm{g}x$ oraz $u\mapsto \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}u$. Jest okresowa o okresie $\pi$ wystarczy więc rozważyć ją np. na przedziale $0<x<\pi$. Ze wzoru redukcyjnego mamy $\mathrm{c}\mathrm{t}\mathrm{g}x=\mathrm{t}\mathrm{g}(\frac{\pi }{2}-x)$, stąd

$\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}(\mathrm{c}\mathrm{t}\mathrm{g}x)=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}\left(\mathrm{t}\mathrm{g}(\frac{\pi }{2}-x)\right)=\frac{\pi }{2}-x,$

dla $0<x<\pi$.

Podobnie $x\mapsto \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{t}\mathrm{g}(\mathrm{t}\mathrm{g}x)$ jest nieparzysta, okresowa o okresie $\pi$. Wystarczy więc rozważyć ją np. w przedziale $(-\frac{\pi }{2},\frac{\pi }{2})$, gdzie zachodzi równość:

$\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{t}\mathrm{g}(\mathrm{t}\mathrm{g}x)=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{t}\mathrm{g}(\mathrm{c}\mathrm{t}\mathrm{g}(\frac{\pi }{2}-x))=\frac{\pi }{2}-x.$

d) Pamiętając, że $\mathrm{t}\mathrm{g}u=\frac{1}{\mathrm{c}\mathrm{t}\mathrm{g}u}$, otrzymamy $\mathrm{t}\mathrm{g}(\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{t}\mathrm{g}x)=\frac{1}{\mathrm{c}\mathrm{t}\mathrm{g}(\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{t}\mathrm{g}x)}=\frac{1}{x}$, dla $x\ne 0$.

Podobnie: $\mathrm{c}\mathrm{t}\mathrm{g}(\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}x)=\frac{1}{\mathrm{t}\mathrm{g}(\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}x)}=\frac{1}{x}$, dla $x\ne 0$.
e) Z jedynki hiperbolicznej $\sinh (u)=\sqrt{{\cosh }^{2}u-1}$ dla $u\ge 0$. Po podstawieniu $u:=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x$, dostajemy $\sinh (\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)=\sqrt{x^2-1}$, dla $x\ge 1$.

Z kolei ${\cosh }^{2}v=1+{\sinh }^{2}v$. Funkcja $x\mapsto \cosh (\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}x)$ jest określona na całym zbiorze liczb rzeczywistych i jest parzysta. Mamy równość:

$\cosh (\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}x)=\sqrt{1+{\sinh }^2(\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}x)}=\sqrt{1+x^2},$

prawdziwą dla wszystkich liczb rzeczywistych $x$.

Ćwiczenie 2.4.

Wykazać, że dla dowolnych liczb $x$, $y$ zachodzą równości:
a) $\cosh (x+y)=\cosh x\cosh y+\sinh x\sinh y$,
b) $\sinh (x+y)=\sinh x\cosh y+\cosh x\sinh y$.

Wskazówka

a) Warto przekształcić wpierw prawą stronę równości, skorzystać z definicji funkcji $\sinh$ oraz $\cosh$, wykonać mnożenie i zredukować wyrazy podobne.
b) Należy postąpić podobnie jak w punkcie a) zadania.

Rozwiązanie

a) Z definicji funkcji $\sinh$ i $\cosh$ mamy:

$\begin{array}{rl}4(\cosh x\cosh y+\sinh x\sinh y)& =(e^x+e^{-x})(e^y+e^{-y})(e^x-e^{-x})(e^y-e^{-y})\\ & =e^{x+y}+e^{x-y}+e^{-x+y}+e^{-x-y}+e^{x+y}-e^{x-y}-e^{-x+y}+e^{-x-y}\\ & =2(e^{x+y}+e^{-(x+y)})\\ & =4\cosh (x+y),\end{array}$

stąd $\cosh x\cosh y+\sinh x\sinh y=\cosh (x+y)$.

b) Dokonując podobnych przekształceń jak w punkcie a), otrzymujemy:

$\begin{array}{rl}4(\sinh x\cosh y+\cosh x\sinh y)& =(e^x-e^{-x})(e^y+e^{-y})(e^x+e^{-x})(e^y-e^{-y})\\ & =e^{x+y}+e^{x-y}-e^{-x+y}-e^{-x-y}+e^{x+y}-e^{x-y}{+}^{-x+y}-e^{-x-y}\\ & =2(e^{x+y}-e^{-(x+y)})\\ & =4\sinh (x+y),\end{array}$

stąd $\sinh x\cosh y+\cosh x\sinh y=\sinh (x+y)$.

Ćwiczenie 2.5.

a) Niech $T_n(x):=\cos (n\arccos x)$ dla $n=0,1,2,.$... Wykaż, że $T_0(x)=1$, $T_1(x)=x$ oraz

$T_{n+2}(x)=2x{T}_{n+1}(x)-T_n(x),$

dla $n\ge 0$.
b) Wykazać, że funkcja $T_n(x)=\cos (n\arccos x)$ jest wielomianem zmiennej $x$, dla $n=0,1,2,3,.$...

Wskazówka

a) Przekształcić $T_{n+2}$ oraz $T_{n+1}$, wykorzystując wzory wyrażające sinus i cosinus sumy $x+y$, analogiczne do tych, które zostały wykazane w ćwiczeniu 2.4., a mianowicie:

$\begin{array}{rl}\cos (x+y)& =\cos x\cos y-\sin x\sin y,\\ \sin (x+y)& =\sin x\cos y+\cos x\sin y.\end{array}$

b) Suma i iloczyn wielomianów jest wielomianem. Wykorzystać formułę z punktu a) zadania.

Rozwiązanie

a) Niech $y:=\arccos x$. Stosując znane wzory na cosinus i sinus sumy $x+y$ oraz jedynkę trygonometryczną, otrzymamy

$\begin{array}{rl}{T}_{n+2}(x)& =\cos (ny+2y)\\ & =\cos (ny)\cos (2y)-\sin (ny)\sin (2y)\\ & =\cos (ny)(2{\cos }^{}y-1)-\sin (ny)2\sin y\cos y\\ & =T_n(x)(2x^2-1)-2x\sin (n\arccos x)\sin (\arccos x),\end{array}$

gdyż $\cos y=\cos (\arccos x)=x$ oraz $\cos ny=\cos (n\arccos x)=T_n(x)$. Przekształćmy także

$\begin{array}{rl}{T}_{n+1}(x)& =\cos (ny+y)\\ & =\cos (ny)\cos (y)-\sin (ny)\sin (y)\\ & =T_n(x)x-\sin (n\arccos x)\sin (\arccos x).\end{array}$

Stąd $\sin (n\arccos x)\sin (\arccos x)=x{T}_n(x)-T_{n+1}(x)$. Wobec tego

$\begin{array}{rl}{T}_{n+2}(x)& =T_n(x)(2x^2-1)-2x\sin (n\arccos x)\sin (\arccos x)\\ & =T_n(x)(2x^2-1)-2x(x{T}_n(x)-T_{n+1}(x))\\ & =2x{T}_{n+1}(x)-T_n(x).\end{array}$

b) Formuła wykazana w punkcie b) pozwala wyznaczyć $T_{n+2}$ dla $n=0,1,2,.$... Iloczyn i suma wielomianów jest wielomianem. Funkcje $T_0(x)=1$ oraz $T_1(x)=x$ są wielomianami zmiennej $x$, więc każda kolejna funkcja

$\begin{array}{rlrlr}{T}_2(x)& =2x{T}_1(x)-T_0(x)=2x^2-1,T_3(x)& =2x{T}_2(x)-T_1(x)=4x^3-3x,T_4(x)& =2x{T}_3(x)-T_2(x)=8x^4-8x^2+1,T_5(x)& =2x{T}_4(x)-T_3(x)=16x^5-20x^3+5x,...\end{array}$

jest również wielomianem zmiennej $x$.

Ćwiczenie 2.6.

a) Niech $U_n(x):=\cosh (n\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)$ dla $n=0,1,2,.$... Wykaż, że $U_0(x)=1$, $U_1(x)=x$ oraz

$U_{n+2}(x)=2x{U}_{n+1}(x)-U_n(x),$
dla $n\ge 0$.

b) Wykazać, że funkcja $U_n(x)=\cosh (n\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)$ jest wielomianem zmiennej $x$, dla $n=0,1,2,3,.$...
c) Wykazać, że dla dowolnej liczby $n=0,1,2,3,.$.. istnieje wielomian $W_n$ taki, że $U_n$ oraz $T_n$ są restrykcjami - odpowiednio do przedziałów $[1,\mathrm{\infty })$ oraz $[-1,1]$ - wielomianu $W_n$.

Wskazówka

a) Warto uprościć $U_{n+2}$ oraz $U_{n+1}$, wykorzystując wzory wykazane w ćwiczeniu 2.4.
b) Suma i iloczyn wielomianów jest wielomianem. Wykorzystać formułę z punktu a) zadania.
c) Porównać formuły z punktów b) w ćwiczeniu 2.5. i ćwiczeniu 2.6. Wyznaczyć dziedziny funkcji $T_n$ oraz $U_n$.

Rozwiązanie

Niech $y:=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x$. Postępując podobnie jak w ćwiczeniu 2.5. tzn. stosując wykazane w ćwiczeniu 2.4. wzory na cosinus hiperboliczny i sinus hiperboliczny sumy $x+y$ oraz jedynkę hiperboliczną, otrzymamy

$\begin{array}{rl}{U}_{n+2}(x)& =\cosh (ny+2y)\\ & =\cosh (ny)\cosh (2y)+\sinh (ny)\sinh (2y)\\ & =\cosh (ny)(2{\cosh }^{}y-1)+\sinh (ny)2\sinh y\cosh y\\ & =U_n(x)(2x^2-1)+2x\sinh (n\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)\sinh (\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x),\end{array}$

gdyż $\cosh y=\cosh (\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)=x$ oraz $\cosh (ny)=\cosh (n\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)=U_n(x)$. Przekształćmy także

$\begin{array}{rl}{U}_{n+1}(x)& =\cosh (ny+y)\\ & =\cosh (ny)\cosh (y)+\sinh (ny)\sinh (y)\\ & =U_n(x)x+\sinh (n\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)\sinh (\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x).\end{array}$

Stąd $\sinh (n\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)\sinh (\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)=-x{U}_n(x)+U_{n+1}(x)$. Wobec tego

$\begin{array}{rl}{U}_{n+2}(x)& =U_n(x)(2x^2-1)+2x\sinh (n\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)\sinh (\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)\\ & =U_n(x)(2x^2-1)+2x(-x{U}_n(x)+U_{n+1}(x))\\ & =2x{U}_{n+1}(x)-U_n(x).\end{array}$

b) Zauważmy, że formuła wykazana w punkcie b) pozwala wyznaczyć $U_{n+2}$ dla $n=0,1,2,.$... Iloczyn i suma wielomianów jest wielomianem. Ponadto funkcje $U_0(x)=1$ oraz $U_1(x)=x$ są wielomianami zmiennej $x$, więc każda kolejna funkcja

$\begin{array}{rl}{U}_2(x)& =2x{U}_1(x)-U_0(x)=2x^2-1,\\ U_3(x)& =2x{U}_2(x)-U_1(x)=4x^3-3x,\\ U_4(x)& =2x{U}_3(x)-U_2(x)=8x^4-8x^2+1,\\ U_5(x)& =2x{U}_4(x)-U_3(x)=16x^5-20x^3+5x,...\end{array}$

jest również wielomianem zmiennej $x$.
c) Formuły pozwalające wyznaczyć $T_{n+2}$ oraz $U_{n+2}$ są identyczne:

$\begin{array}{rl}{T}_{n+2}(x)& =2x{T}_{n+1}(x)-T_n,T_0(x)=1,T_1(x)=x,\\ U_{n+2}(x)& =2x{U}_{n+1}(x)-U_n,U_0(x)=1,U_1(x)=x.\end{array}$

Wielomiany $T_n$ oraz $U_n$ są więc zacieśnieniem -- odpowiednio do przedziałów $[-1,1]$ oraz $[1,\mathrm{\infty })$ - tego samego wielomianu
$W_n$, $n=0,1,2,.$... Zwróćmy uwagę na fakt, że dziedziną każdej z funkcji $T_n(x)=\cos (n\arccos x)$ jest przedział $[-1,1]$ a dziedziną funkcji $U_n(x)=\cosh (n\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}x)$ - przedział $[1,+\mathrm{\infty })$. Stąd formalnie równość funkcji $T_n(x)=U_n(x)$ ma sens w części wspólnej obu dziedzin, tj. w punkcie $x=1$.