PEE Moduł 9: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „,</math>” na „</math>,” |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| Linia 203: | Linia 203: | ||
: <math>T(j\omega)=T(s)|_{s=j\omega}</math> | : <math>T(j\omega)=T(s)|_{s=j\omega}</math> | ||
Transmitancja widmowa reprezentuje sobą liczbę zespoloną będącą funkcją pulsacji <math>\omega\</math>,. Przedstawiając ją w postaci wykładniczej, to jest <math>T(j\omega)=|T(j\omega)|e^{j\varphi (\omega)}</math> można zdefiniować dwa rodzaje charakterystyk częstotliwościowych: | Transmitancja widmowa reprezentuje sobą liczbę zespoloną będącą funkcją pulsacji <math>\omega\ </math>,. Przedstawiając ją w postaci wykładniczej, to jest <math>T(j\omega)=|T(j\omega)|e^{j\varphi (\omega)}</math> można zdefiniować dwa rodzaje charakterystyk częstotliwościowych: | ||
* '''charakterystyka amplitudowa''' przedstawia sobą zależność modułu transmitancji widmowej <math>T(j\omega)</math> od pulsacji <math>\omega\</math>, (częstotliwości f), to jest <math>|T(j\omega)|</math> | * '''charakterystyka amplitudowa''' przedstawia sobą zależność modułu transmitancji widmowej <math>T(j\omega)</math> od pulsacji <math>\omega\ </math>, (częstotliwości f), to jest <math>|T(j\omega)|</math> | ||
* '''charakterystyka fazowa''' określa zależność argumentu transmitancji widmowej <math>T(j\omega)</math> od pulsacji (częstotliwości) to jest <math>\varphi (\omega)</math>. Charakterystyka fazowa reprezentuje sobą przesunięcie fazowe między sygnałem wejściowym a wyjściowym dla danej pulsacji <math>\omega\</math>,. | * '''charakterystyka fazowa''' określa zależność argumentu transmitancji widmowej <math>T(j\omega)</math> od pulsacji (częstotliwości) to jest <math>\varphi (\omega)</math>. Charakterystyka fazowa reprezentuje sobą przesunięcie fazowe między sygnałem wejściowym a wyjściowym dla danej pulsacji <math>\omega\ </math>,. | ||
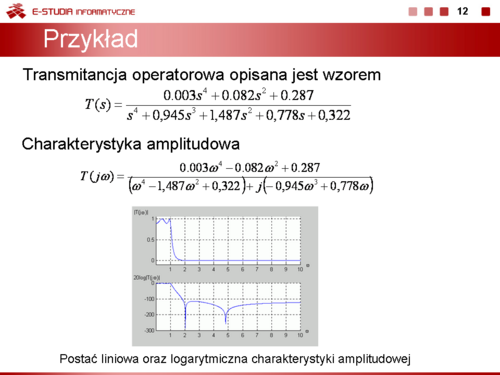
Charakterystyki częstotliwościowe przedstawia się zwykle na wykresie modułu lub fazy w zależności od pulsacji (częstotliwości). Jeśli wielkości podlegające wykreślaniu różnią się znacznie pod względem wartości (np. zmieniają się w zakresie od <math>1\</math>, do <math>10^6</math>) wygodnie jest wprowadzić skalę logarytmiczną zwykle o podstawie 10. Dotyczy to określonego zakresu częstotliwości. W przypadku charakterystyki amplitudowej skalę logarytmiczną przelicza się na decybele (dB) definiując '''logarytmiczną charakterystykę amplitudową''' | Charakterystyki częstotliwościowe przedstawia się zwykle na wykresie modułu lub fazy w zależności od pulsacji (częstotliwości). Jeśli wielkości podlegające wykreślaniu różnią się znacznie pod względem wartości (np. zmieniają się w zakresie od <math>1\ </math>, do <math>10^6</math>) wygodnie jest wprowadzić skalę logarytmiczną zwykle o podstawie 10. Dotyczy to określonego zakresu częstotliwości. W przypadku charakterystyki amplitudowej skalę logarytmiczną przelicza się na decybele (dB) definiując '''logarytmiczną charakterystykę amplitudową''' | ||
: <math>20log_{10}(|T(j\omega)|)</math> | : <math>20log_{10}(|T(j\omega)|)</math> | ||
| Linia 341: | Linia 341: | ||
Załączony do podręcznika program interakcyjny '''CHARAKTERYSTYKI''' umożliwia wykreślanie charakterystyk częstotliwościowych (amplitudowych i fazowych) układów opisanych za pomocą transmitancji operatorowej o postaci określonej wzorem powyższym. | Załączony do podręcznika program interakcyjny '''CHARAKTERYSTYKI''' umożliwia wykreślanie charakterystyk częstotliwościowych (amplitudowych i fazowych) układów opisanych za pomocą transmitancji operatorowej o postaci określonej wzorem powyższym. | ||
Transmitancja widmowa <math>T(j\omega)</math> takiego układu wyznaczana jest z transmitancji operatorowej <math>T(s)\</math>, przez podstawienie <math>s=j\omega</math>. W wyniku otrzymuje się | Transmitancja widmowa <math>T(j\omega)</math> takiego układu wyznaczana jest z transmitancji operatorowej <math>T(s)\ </math>, przez podstawienie <math>s=j\omega</math>. W wyniku otrzymuje się | ||
: <math>T(s)=\frac{b_m(j\omega)^m+b_{m-1}(j\omega)^{m-1}+...+b_1j\omega+b_0}{a_n(j\omega)^n+a_{n-1}(j\omega)^{n-1}+...+a_1j\omega+a_0}</math> | : <math>T(s)=\frac{b_m(j\omega)^m+b_{m-1}(j\omega)^{m-1}+...+b_1j\omega+b_0}{a_n(j\omega)^n+a_{n-1}(j\omega)^{n-1}+...+a_1j\omega+a_0}</math> | ||
| Linia 349: | Linia 349: | ||
: <math>T(j\omega)=A(\omega)+jB(\omega)</math> | : <math>T(j\omega)=A(\omega)+jB(\omega)</math> | ||
Część rzeczywista <math>A(\omega)</math> i urojona <math>B(\omega)</math> są funkcjami zarówno współczynników <math>a_i</math>, <math>b_i</math> licznika i mianownika transmitancji operatorowej, jak i aktualnej wartości pulsacji <math>\omega\</math>,. Charakterystyka amplitudowa przedstawia sobą moduł transmitancji widmowej określony wzorem | Część rzeczywista <math>A(\omega)</math> i urojona <math>B(\omega)</math> są funkcjami zarówno współczynników <math>a_i</math>, <math>b_i</math> licznika i mianownika transmitancji operatorowej, jak i aktualnej wartości pulsacji <math>\omega\ </math>,. Charakterystyka amplitudowa przedstawia sobą moduł transmitancji widmowej określony wzorem | ||
: <math>|T(j\omega)|=\sqrt{A^2(\omega)+B^2(\omega)}</math> | : <math>|T(j\omega)|=\sqrt{A^2(\omega)+B^2(\omega)}</math> | ||
| Linia 374: | Linia 374: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd17.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd17.png|500px]] | ||
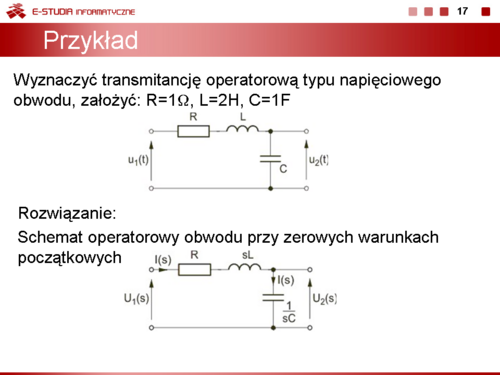
|valign="top"|Jako przykład wyznaczymy transmitancję operatorową typu napięciowego obwodu (górny rysunek na slajdzie obok). Przyjmijmy: <math>R=1\Omega</math>, <math>L=2H\</math>,, <math>C=1F\</math>,. | |valign="top"|Jako przykład wyznaczymy transmitancję operatorową typu napięciowego obwodu (górny rysunek na slajdzie obok). Przyjmijmy: <math>R=1\Omega</math>, <math>L=2H\ </math>,, <math>C=1F\ </math>,. | ||
| Linia 459: | Linia 459: | ||
Transmitancja widmowa obwodu określona jest na podstawie transmitancji operatorowej <math>T_u(s)\</math>, przy założeniu <math>s=j\omega</math> | Transmitancja widmowa obwodu określona jest na podstawie transmitancji operatorowej <math>T_u(s)\ </math>, przy założeniu <math>s=j\omega</math> | ||
: <math>T_u(j\omega)=\frac{1}{j\omega RC+1}</math> | : <math>T_u(j\omega)=\frac{1}{j\omega RC+1}</math> | ||
| Linia 474: | Linia 474: | ||
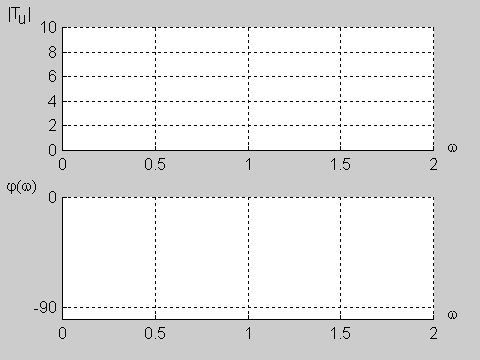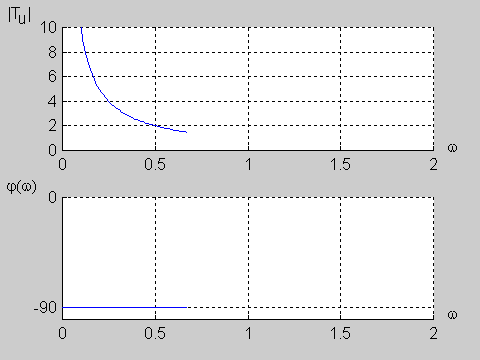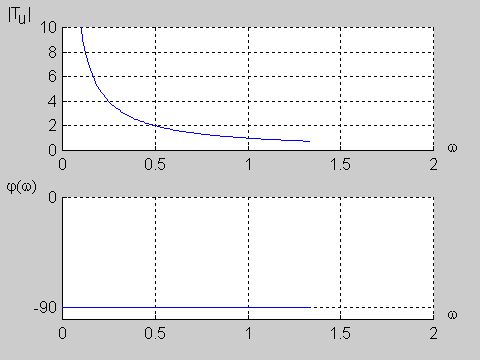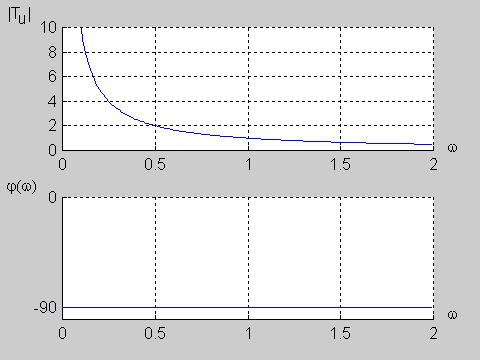
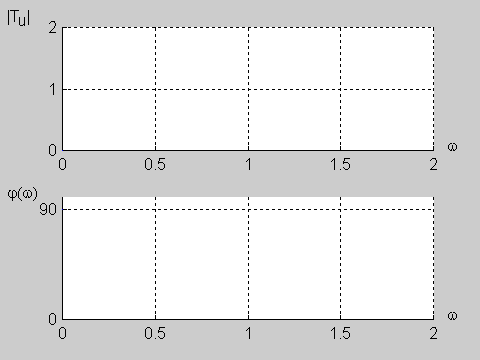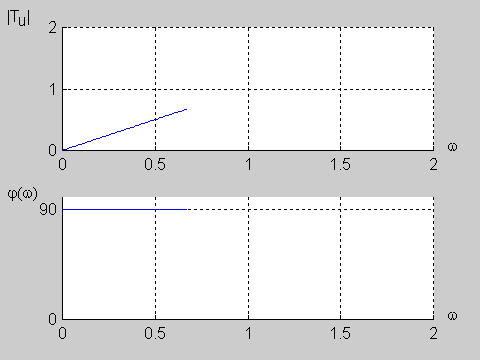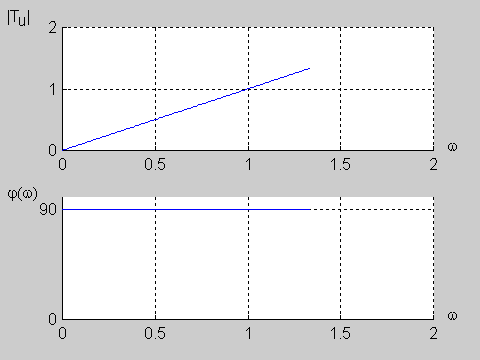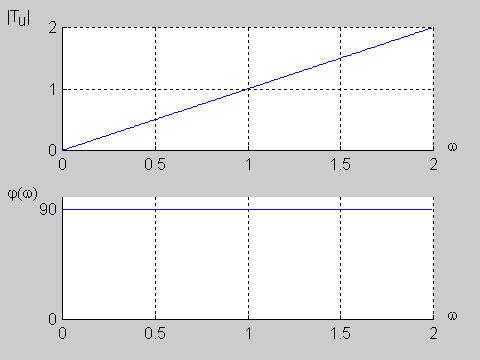
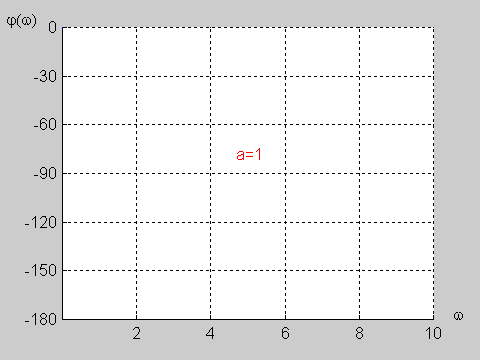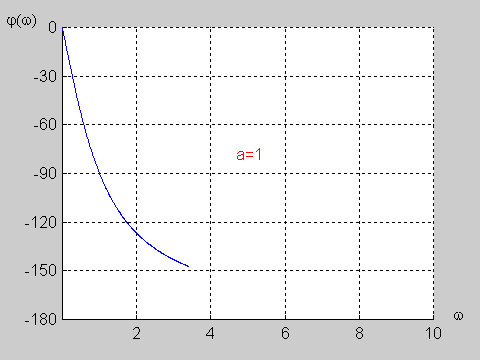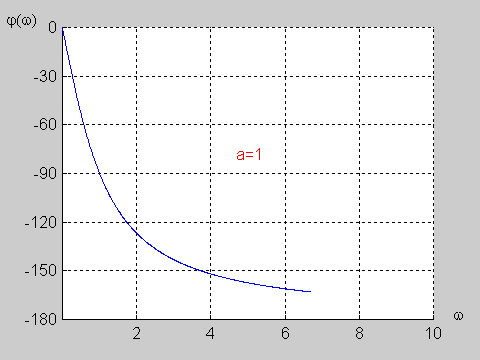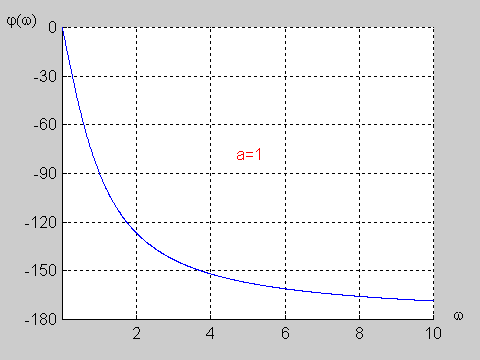
Na poniższym rysunku przedstawiono charakterystykę amplitudową i fazową dla wartości jednostkowych elementów obwodu (<math>R=1\Omega</math> i <math>C=1F\</math>,) | Na poniższym rysunku przedstawiono charakterystykę amplitudową i fazową dla wartości jednostkowych elementów obwodu (<math>R=1\Omega</math> i <math>C=1F\ </math>,) | ||
{| | {| | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_rys_9_10.gif]] | |valign="top" width="500px"|[[Grafika:PEE_M9_rys_9_10.gif]] | ||
|} | |} | ||
Aktualna wersja na dzień 12:04, 5 wrz 2023

|
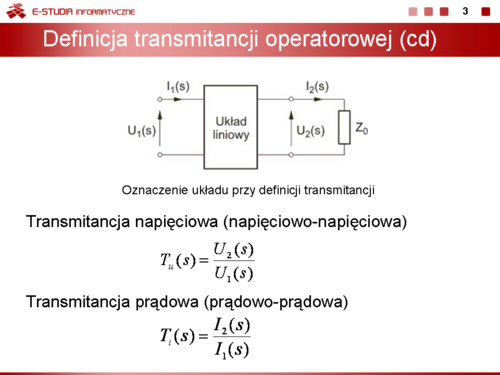
Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów |
|
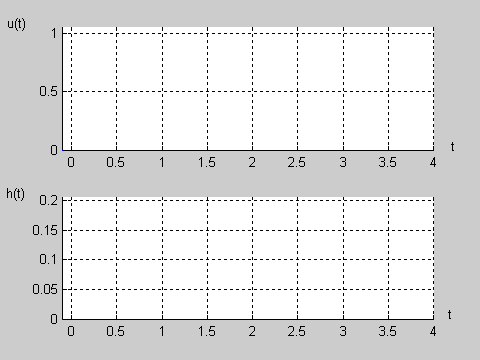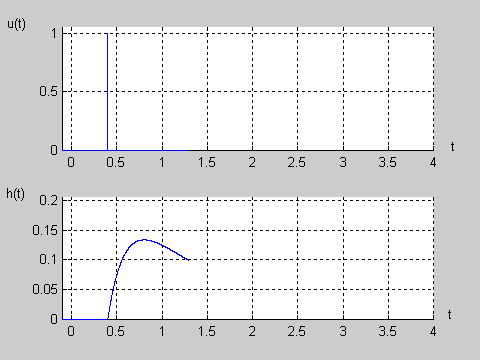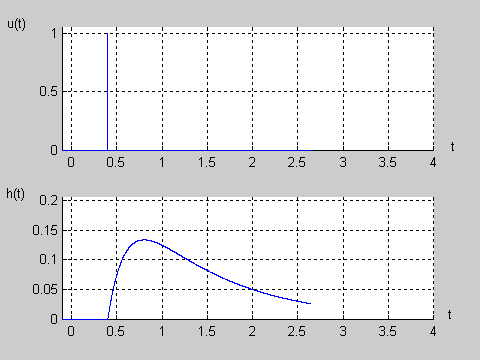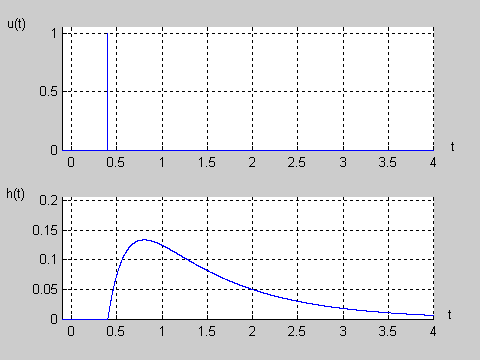
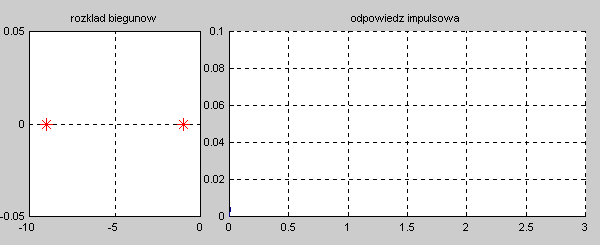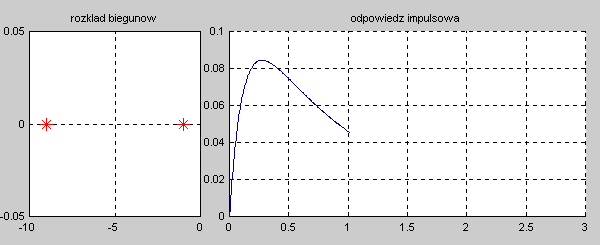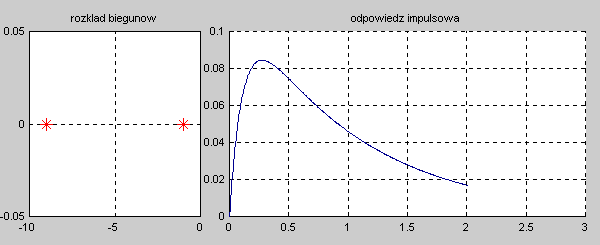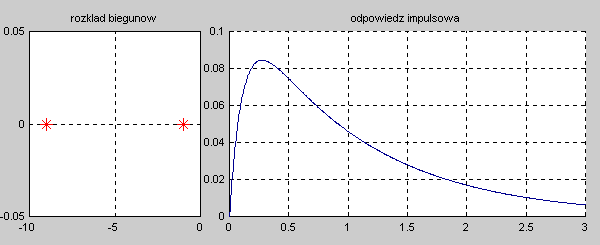
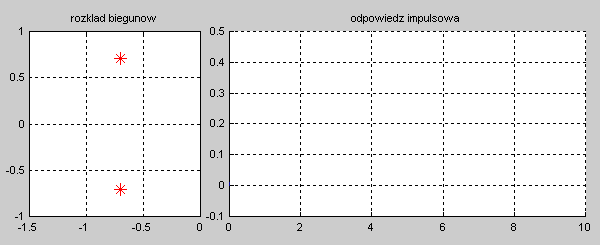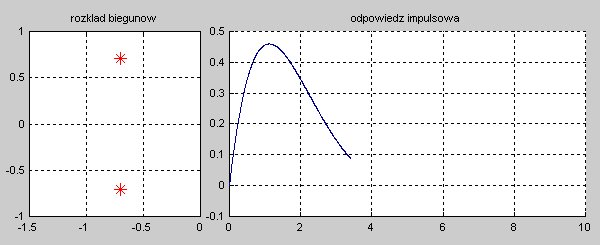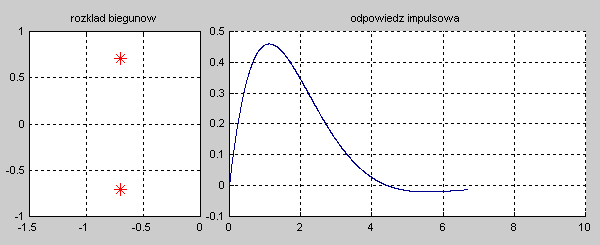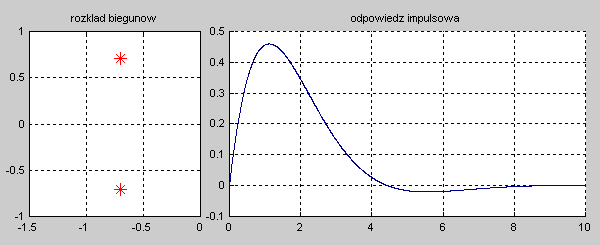
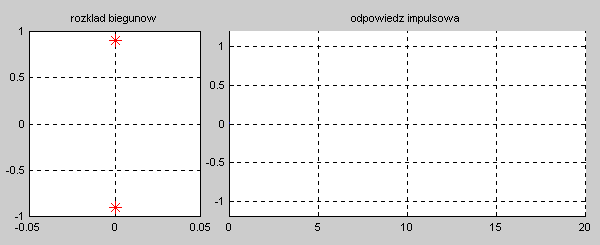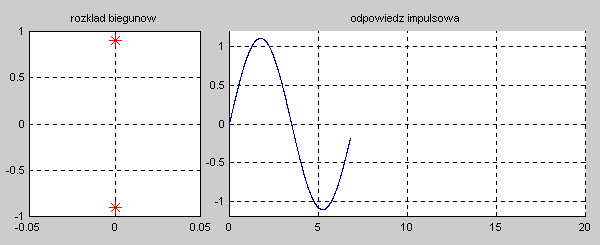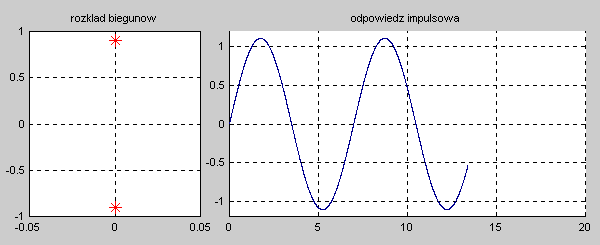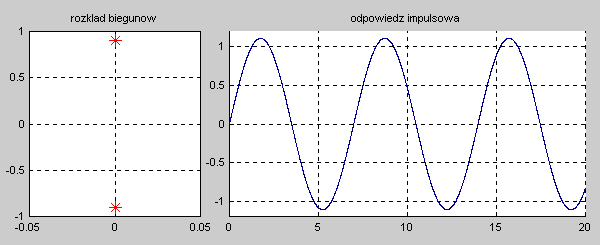
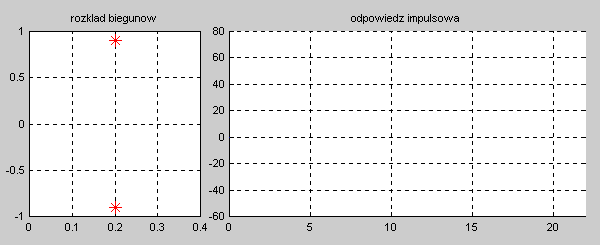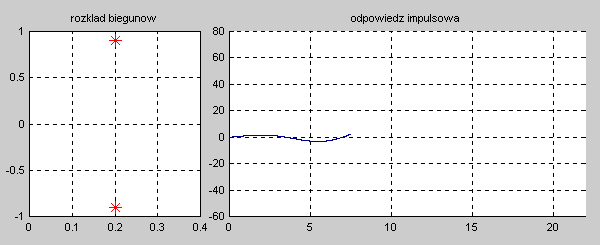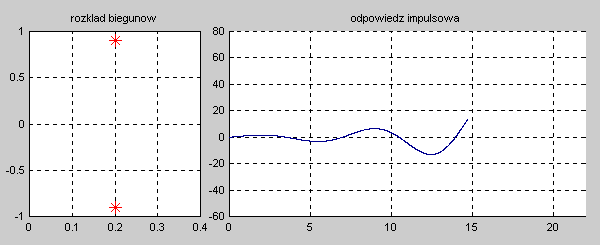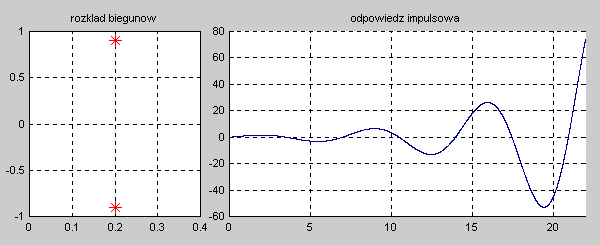
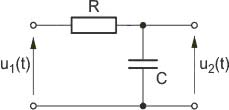
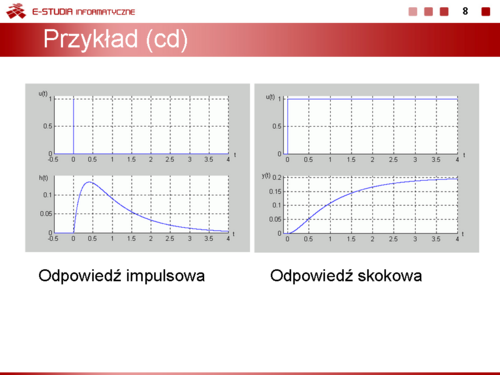
Na slajdzie obok i animacjach poniżej przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej . |

|
Najbardziej ogólnym przypadkiem jest układ opisany transmitancją operatorową T(s) n-tego rzędu o postaci ogólnej zadanej wzorem
Załączony do podręcznika program interakcyjny CHARAKTERYSTYKI umożliwia wykreślanie charakterystyk częstotliwościowych (amplitudowych i fazowych) układów opisanych za pomocą transmitancji operatorowej o postaci określonej wzorem powyższym. Transmitancja widmowa takiego układu wyznaczana jest z transmitancji operatorowej , przez podstawienie . W wyniku otrzymuje się Transmitancja widmowa przedstawia sobą funkcję zespoloną pulsacji i może być zapisana w postaci ogólnej jako Część rzeczywista i urojona są funkcjami zarówno współczynników , licznika i mianownika transmitancji operatorowej, jak i aktualnej wartości pulsacji ,. Charakterystyka amplitudowa przedstawia sobą moduł transmitancji widmowej określony wzorem Charakterystyka fazowa jest fazą transmitancji widmowej i wyznaczana jest z zależności |
| <applet code="filtr.class" archive="images/6/6a/PEE_M9_filtr.jar" width="462" height="363">
</applet> |
Omawiane zależności zostały wykorzystane do badania charakterystyk częstotliwościowych układów opisanych transmitancją operatorową zadawaną przez użytkownika.
Użytkownik ustala stopień licznika i mianownika transmitancji, a także wartości wszystkich współczynników wielomianu licznika i mianownika. Określa również zakres pulsacji, dla którego wykreślane będą charakterystyki częstotliwościowe. W programie założono, że maksymalny rząd układu nie powinien przekroczyć wartości 9. Wykorzystując podane wcześniej zależności częstotliwościowe program wykreśla charakterystyki amplitudowe (liniową i logarytmiczną wyrażoną w decybelach) oraz charakterystykę fazową w stopniach. Charakterystyki filtru zostają wykreślone w oddzielnych oknach, pozwalających na skalowanie oraz oglądanie w powiększeniu poszczególnych odcinków krzywych. |
|
Jako przykład wyznaczymy transmitancję operatorową typu napięciowego obwodu (górny rysunek na slajdzie obok). Przyjmijmy: , ,, ,.
|

|
Kolejne etapy wyznaczania transmitancji:
Prąd I(s) Napięcie wyjściowe Transmitancja napięciowa Po podstawieniu wartości liczbowych otrzymuje się |
| Zadania sprawdzające
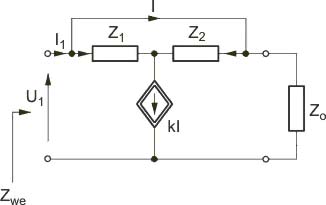
Wyznaczyć impedancję wejściową w postaci operatorowej dla obwodu przedstawionego na poniższym rysunku. Impedancję wejściową potraktować jako transmitancję napięciowo-prądową.
Rozwiązanie Z prawa prądowego i napięciowego Kirchhoffa napisanych dla obwodu z powyzszego rysunku otrzymuje się
Zadanie 9.2 Wyznaczyć charakterystyki częstotliwościowe obwodu przedstawionego na poniższym rysunku biorąc pod uwagę transmitancję napięciową.
Transmitancja napięciowa obwodu określona jest wzorem
|