PEE Moduł 3

---

Moc chwilowa Wartość chwilową napięcia i prądu gałęzi oznaczymy odpowiednio przez $u(t)=U_{m}sin(\omega t)$ oraz $i(t)=I_{m}sin(\omega t-\phi )$ przyjmując dla uproszczenie fazę początkową napięcia równą zeru. Moc chwilowa $p(t)$, jako jedyna z mocy jest funkcją czasu i definiuje się ją w postaci iloczynu wartości chwilowych prądu $i(t)$ oraz $u(t)$ napięcia w obwodzie $p(t)=u(t)i(t)$ Przy wymuszeniu sinusoidalnym moc chwilowa opisana jest wzorem Parser nie mógł rozpoznać (nieznana funkcja „\varphp”): {\displaystyle p(t)=u(t)i(t)=U_mI_m sin(\omega t)sin(\omega t-\varphi)=\frac{U_mI_m}{2}[cos\varphp-cos(2\omega t-\varphi)]=|U||I|[cos \varphi-cos(2\omega t- \varphi)]}

---

Moc czynna Moc czynną definiuje się jako wartość średnią za okres z mocy chwilowej, to jest $P=\frac{1}{T}\underset{t_0}{\overset{t_0+T}{\int }}p(t)dt$ Podstawiając do powyższego wzoru funkcję określającą moc chwilową w obwodzie, po wykonaniu operacji całkowania otrzymuje się $P=|U||I|cos\phi$ Moc czynna w obwodzie o wymuszeniu sinusoidalnym jest więc wielkością stałą równą iloczynowi modułów wartości skutecznych napięcia i prądu oraz cosinusa kąta przesunięcia fazowego między wektorem napięcia i prądu. Współczynnik $cos\phi$ odgrywa ogromną rolę w praktyce i nosi specjalną nazwę współczynnika mocy.

---

Moc czynna stanowi składową stałą mocy chwilowej. Jest ona nieujemna dla obwodu RLC a w granicznym przypadku przy $\phi =\pm \pi /2\to P_L=P_C=0$ jest równa zeru. Moc czynna osiąga wartość największą $P=|U||I|$ wtedy, gdy $\phi =0$ to znaczy gdy odbiornik ma charakter rezystancyjny, $cos\phi =1$ Wartość najmniejszą $(P=0)$ moc osiąga w przypadku granicznym, gdy $\phi =\pm \pi /2$ to znaczy gdy odbiornikiem jest cewka idealna lub kondensator idealny, $cos\phi =0$ Oznacza to, że na elementach reaktancyjnych nie wydziela się moc czynna. Z przytoczonych rozważań wynika, moc czynną wydzielaną w rezystorze można opisać następujacymi wzorami $P=|U||I|cos\phi =R|I{|}^2=G|U{|}^2$ w których prąd $I$, oraz napięcie $U$, odpowiadają rezystorowi $R$,. Jednostką mocy czynnej jest wat ($W)$, przy czym $1W=1AV$. W praktyce stosuje się również wielokrotności wata w postaci kilowata $(1kW=1000W)$ lub megawata $(1MW=10^{6}W)$ oraz wartości ułamkowe, np. miliwat $(mW)$ lub mikrowat $(\mu W)$ Do pomiaru mocy czynnej służy watomierz. Klasyczny watomierz jest przyrządem pomiarowym posiadającym cewkę prądową (o impedancji wewnętrznej bliskiej zeru) do pomiaru prądu gałęziowego obwodu i cewkę napięciową (o impedancji wewnętrznej bliskiej nieskończoności) do pomiaru napięcia między punktami obwodu, dla którego mierzymy moc czynną. Początki uzwojeń obu cewek oznaczać będziemy na schematach przy pomocy gwiazdek. Znak gwiazdki przy cewce prądowej wskazuje kierunek prądu $I_w$ watomierza przyjęty za dodatni (prąd płynie od gwiazdki do watomierza). W przypadku cewki napięciowej gwiazdka wskazuje przyjęty kierunek wyższego potencjału (napięcia $U_w$) obwodu. Wskazanie watomierza jest wówczas określone wzorem , które przy naszych oznaczeniach prądu i napięcia watomierza przyjmą postać $P=|U_w||I_w|cos\phi$ Przyjmując założenie idealizujące, że impedancja cewki prądowej watomierza jest równa zeru a cewki napięciowej równa nieskończoności watomierz nie ma żadnego wpływu na rozpływy prądów i rozkłady napięć w badanym obwodzie elektrycznym.

---

Moc bierna W obwodach elektrycznych prądu sinusoidalnego definiuje się trzecią wielkość energetyczną będącą iloczynem napięcia i prądu oraz sinusa kąta przesunięcia fazowego między nimi. Wielkość ta oznaczana jest literą $Q$ i nazywana mocą bierną $Q=|U||I|sin\phi$ Jednostką mocy biernej jest war (var) będący skrótem nazwy woltamper reaktywny. W przypadku rezystora, dla którego przesunięcie fazowe jest równe zeru $(\phi =0\to Q_R=0)$ moc bierna jest zerowa Moc bierna może się więc wydzielać jedynie na elementach reaktancyjnych, gdyż tylko dla nich przesunięcie fazowe prądu i napięcia jest różne od zera. Przesunięcie fazowe prądu i napięcia na elementach reaktancyjnych (cewce i kondensatorze) przyjmuje wartość $+90$ dla cewki oraz $-90$ dla kondensatora, co oznacza, że sinus kąta jest odpowiednio równy $+1$ dla cewki (moc bierna cewki jest uważana za dodatnią) oraz Parser nie mógł rozpoznać (błąd składni): {\displaystyle –1} dla kondensatora (moc bierna kondensatora jest uważana za ujemną). Stąd przy pominięciu znaku wzór na moc bierną elementów reaktancyjnych o reaktancji $X$ może być przedstawiony w trzech równorzędnych postaciach $|Q|=||U|\cdot |I|\cdot sin\phi |=X|I{|}^2=\frac{1}{X}|U{|}^2$ W ogólności kąt przesunięcia fazowego $\phi$ uważa się za dodatni dla obwodów o charakterze indukcyjnym (napięcie wyprzedza prąd) a za ujemny dla obwodów o charakterze pojemnościowym (napięcie opóźnia się względem prądu). Moc bierna obwodów o charakterze indukcyjnym jest w sumie mocą indukcyjną, kojarzona z liczbą dodatnią a moc bierna obwodów o charakterze pojemnościowym jest więc w sumie mocą pojemnościową i kojarzoną z liczbą ujemną.

---

Moc pozorna zespolona Czwartym rodzajem mocy wprowadzanym w obwodach elektrycznych jest tak zwana moc pozorna zespolona. Jest ona proporcjonalna do wartości skutecznych prądu i napięcia, i oznaczana literą $S$. Moc pozorna zespolona definiowana jest formalnie jako liczba zespolona w postaci iloczynu wartości skutecznej zespolonej napięcia $U$ i wartości skutecznej sprzężonej prądu $I$.

---

Zależność na moc pozorną zespoloną można przedstawić również w postaci wykładniczej $S=|S|e^j{}^{\phi }$ W zależności tej $|S|$ wyraża moduł mocy pozornej zespolonej, który może być wyrażony w postaci iloczynu modułów wartości skutecznych prądu i napięcia $|S|=|U||I|=\sqrt{P^2+Q^2}$ Z wykresu wektorowego obwodu przedstawionego na rysunku możliwe jest wyznaczenie współczynnika mocy. Mianowicie $cos\phi =\frac{P}{|S|}$ Wartość współczynnika mocy wyznaczona z powyższej zależności jest identyczna z wartością wynikającą z relacji prądowo-napięciowych zachodzących dla wielkości bramowych obwodu.

---

Dla ułatwienia korzystania z pojęć mocy zestawiono poniżej najważniejsze postacie wzorów na moc czynną, bierną i pozorną Moc pozorna zespolona $S=U{I}^{*}=P+jQ$ Moc czynna $P=Re(S)=|U|I|cos\phi =|I_R{|}^{2}R=\frac{|U_R{|}^2}{R}$ Moc bierna $Q=Im(S)=|U||I|sin\phi =\pm |I_X{|}^{2}X=\pm \frac{|U_X{|}^2}{X}$ Znak plus dotyczy mocy biernej cewki a minus kondensatora.

---

Bilans mocy W obwodzie elektrycznym, jak w każdym układzie fizycznym obowiązuje prawo zachowania energii. W przypadku obwodów prawo to przekształca się w tak zwane prawo bilansu mocy. Jeśli całkowitą moc pozorną zespoloną wytworzoną przez źródło (lub wiele źródeł występujących w obwodzie) oznaczymy przez $S_g$, a sumaryczną moc pozorną zespoloną wydzieloną w elementach odbiornika przez $S_o$,, to biorąc pod uwagę prawo zachowania energii obie moce muszą być sobie równe, to znaczy $S_g=S_o$,. Jest to tak zwana zasada bilansu mocy w obwodach elektrycznych. W tak sformułowanej zasadzie bilansu mocy przyjmuje się standardowo, że zwroty prądów i napięć w elementach odbiornikowych są przeciwne sobie a w elementach źródłowych takie same. Jeśli przyjmiemy ujednoliconą zasadę znakowania prądów i napięć na gałęziach obwodu, zakładającą, że niezależnie od rodzaju elementu zwroty prądu i napięcia na gałęzi są przeciwne sobie, to zasadę bilansu mocy można sformułować w ten sposób, że suma mocy pozornej zespolonej liczonej po wszystkich elementach w obwodzie elektrycznym jest równa zeru, $S_g+S_o=0$.

---

<applet code="moce_demo.class" archive="images/a/a9/PEE_M3_moce.jar" width="600" height="580"></applet>

Umieszczony obok program pozwala na analizę w trybie on-line obwodu RLC o strukturze przedstawionej na rysunku. Użytkownik wybiera elementy obwodu włączone w strukturę i wpisuje ich wartości. Po naciśnięciu przycisku OBLICZ program automatycznie obliczy wartości wszystkich prądów, napięć i mocy elementów, podając jednocześnie bilans mocy.

---

Dla zilustrowania wprowadzonych tu pojęć mocy oraz zasady bilansowania się mocy rozpatrzymy przykład obwodu przedstawionego na rysunku. Niech dany będzie obwód RLC o strukturze przedstawionej na rysunku zasilany z sinusoidalnego źródła napięcia $e(t)=100\sqrt{2}sin(\omega t+45^o)$ V o wartości $\omega =1\frac{rad}{s}$. Wartości elementów obwodu są następujące: $R=1\mathrm{\Omega },C=0,5F,L=1H$. Należy wyznaczyć wartości skuteczne zespolone prądów i napięć elementów oraz moce i bilans mocy w obwodzie.

---

Rozwiązanie Wartości zespolone impedancji i napięcia wymuszającego w obwodzie przy danych wartościach elementów są równe: $Z_L=j\omega L=j1,Z_C=-j1/\omega C=-j2,E=100e^j{}^{45^o}$ Impedancja zastępcza połączenia równoległego L i R równa się $Z_R{}_L=\frac{R{Z}_L}{R+Z_L}=0,707e^j{}^{45^o}$ Impedancja zastępcza połączenia szeregowego $Z_C$ i $Z_{RL}$ jest równa $Z=Z_C+Z_{RL}=-j2+0,5+j0,5=1,58e^{-j71,6^o}$

---

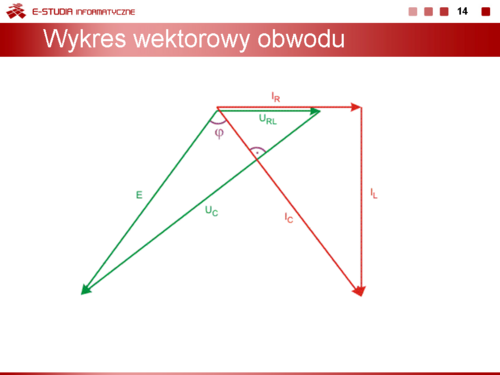
Napięcia na poszczególnych elementach obwodu dane są w postaci $I_C=\frac{E}{Z}=\frac{100e^{j45^o}}{1,58e^{-j71,6^o}}=63,3e^{j116,6^o}$ $U_C=Z_C{I}_C=126,6e^j{}^{26,6^o}$ $U_R{}_L=Z_R{}_L{I}_C=44,72e^j{}^{161,6^o}$ Prądy cewki i rezystora obliczone z prawa Ohma równają się $I_L=\frac{U_R{}_L}{Z_L}=44,72e^j{}^{71,6^o}$ $I_R=\frac{U_R{}_L}{R}=44,72e^j{}^{161,6^o}$

---

Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie.

---

Poszczególne rodzaje mocy wydzielonej w obwodzie równają się: Moc pozorna zespolona wydawana przez źródło $S=E\cdot I_C^{*}=(2000-j6000)V\cdot A$ Moc wydzielana na rezystorze $P_R=R|I_R{|}^2=2000W$ Moc bierna cewki i kondensatora $Q_L=Im(U_R{}_L\cdot I_L^{*})=2000var$ $Q_C=Im(U_C\cdot I_C^{*})=-8000var$ Całkowita moc bierna wydzielona na cewce i kondensatorze równa się $Q=Q_L+Q_C=-6000var$ Moc wydzielona na rezystorze oraz cewce i kondensatorze równa się dokładnie mocy dostarczonej przez źródło. Bilans mocy generowanej przez źródło i mocy wydzielonej w odbiorniku jest zatem równy zeru.

---

Energia magazynowana w idealnym kondensatorze Cewka i kondensator traktowane jako idealne elementy obwodowe należą do elementów magazynujących energię elektryczną. Rozpatrzmy kondensator o pojemności $C$, zasilony z generatora napięciowego $u(t)$,. Obliczymy energię dostarczoną do tego kondensatora w czasie od $t_0$, do $t$,. Energia ta może być obliczona jako całka z mocy chwilowej $W(t_0,t)=\underset{t_0}{\overset{t}{\int }}p(\tau )d\tau$ Uwzględniając wzór na moc chwilową i dokonując odpowiednich operacji całkowania otrzymujemy $W(t_0,t)=\underset{t_0}{\overset{t}{\int }}u(\tau )i(\tau )d\tau =\underset{t_0}{\overset{t}{\int }}u(\tau )C\frac{du(\tau )}{d\tau }d\tau =C\underset{u(t_0)}{\overset{u(t)}{\int }}udu$ Uwzględniając wzór na moc chwilową i dokonując odpowiednich operacji całkowania otrzymujemy $W(t_0,t)=C\underset{0}{\overset{u(t)}{\int }}udu=\frac{1}{2}C{u}^2(t)$ Zasadniczą cechą kondensatora idealnego jest jego bezstratność, co oznacza, że energia zgromadzona na nim pozostaje w nim zmagazynowana. Zatem kondensator naładowany do napięcia stałego U posiada energię równą $W=\frac{1}{2}C{U}^2$ Jest to bardzo ważna własność kondensatora, wykorzystywana do magazynowania energii elektrycznej.

---

Energia magazynowana w idealnej cewce Rozpatrzmy cewkę o indukcyjności $L$, zasiloną z generatora napięciowego $u(t)$,. Obliczymy energię dostarczoną do tej cewki w czasie od $t_0$, do $t$,. Energia ta, podobnie jak w przypadku kondensatora, może być obliczona jako całka z mocy chwilowej $W(t_0,t)=\underset{t_0}{\overset{t}{\int }}p(\tau )d\tau$ Uwzględniając wzór na moc chwilową i dokonując odpowiednich operacji całkowania otrzymujemy $W(t_0,t)=\underset{t_0}{\overset{t}{\int }}u(\tau )i(\tau )d\tau =\underset{t_0}{\overset{t}{\int }}i(\tau )L\frac{di(\tau )}{d\tau }d\tau =L\underset{i(t_0)}{\overset{i(t)}{\int }}idi$ Załóżmy, że czas t0 jest taką chwilą, w której prąd cewki $i(t)$, jest zerowy. W takim razie wzór na energię upraszcza się do postaci $W(t_0,t)=L\underset{0}{\overset{i(t)}{\int }}idi=\frac{1}{2}L{i}^2(t)$ Zasadniczą cechą cewki idealnej jest jej bezstratność, co oznacza, że energia dostarczona do niej pozostaje w niej zmagazynowana. Zatem cewka, przez która przepływa prąd stały I posiada energię równą $W=\frac{1}{2}L{I}^2$ W odróżnieniu od kondensatora, w którym energia związana była z napięciem między okładkami (ładunkiem) energia cewki jest uzależniona od prądu (strumienia magnetycznego). Stąd przyjmuje się, że kondensator magazynuje energię w polu elektrycznym a cewka w polu magnetycznym.

---

Zadania sprawdzające Zadanie 3.1 Sporządzić bilans mocy w obwodzie przedstawionym na rysunku. Przyjąć następujące wartości elementów: $e(t)=50\sqrt{2}sin(\omega t)V,\omega =1\frac{rad}{s},L=10H,C=0,1F,R_1=15\mathrm{\Omega },R_2=10\mathrm{\Omega }$. Rozwiązanie Wartości symboliczne elementów obwodu: $\omega =1$ $E=50$ Parser nie mógł rozpoznać (nieznana funkcja „\omegaL”): {\displaystyle Z_L=j\omegaL=j10} $Z_C=\frac{1}{j\omega C}=-j10$ Impedancje obwodu: $\frac{1}{Z_{AB}}=\frac{1}{R_2}+\frac{1}{Z_L}+\frac{1}{Z_C}=0,1$ $Z_{AB}=10$ $Z=Z_{AB}+R_1=25$ Prądy i napięcia w obwodzie: $I=E/Z=2$ $U_{AB}=I{Z}_{AB}=20$ $I_1=\frac{U_{AB}}{Z_C}=j2$ $I_2=\frac{U_{AB}}{Z_L}=-j2$ $I_3=\frac{U_{AB}}{R_2}=2$ Moc wydawana prze źródło $S_E=E{I}_{*}=50\cdot 2=100+j0$ Moce elementów $P_{R_1}=|I{|}^2{R}_1=60W$ $P_{R_2}=|I_3{|}^2{R}_2=40W$ $Q_L=|I_2{|}^2\omega L=40var$ $Q_C=-|I_1{|}^2\frac{1}{\omega C}=-40var$ Moc całkowita odbiornika $S_{odb}=P_{R_1}+P_{R_2}+j{Q}_L+j{Q}_C=100+j0$ Moc odbiornika jest dokładnie równa mocy źródła.