PEE Moduł 9: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 40: | Linia 40: | ||
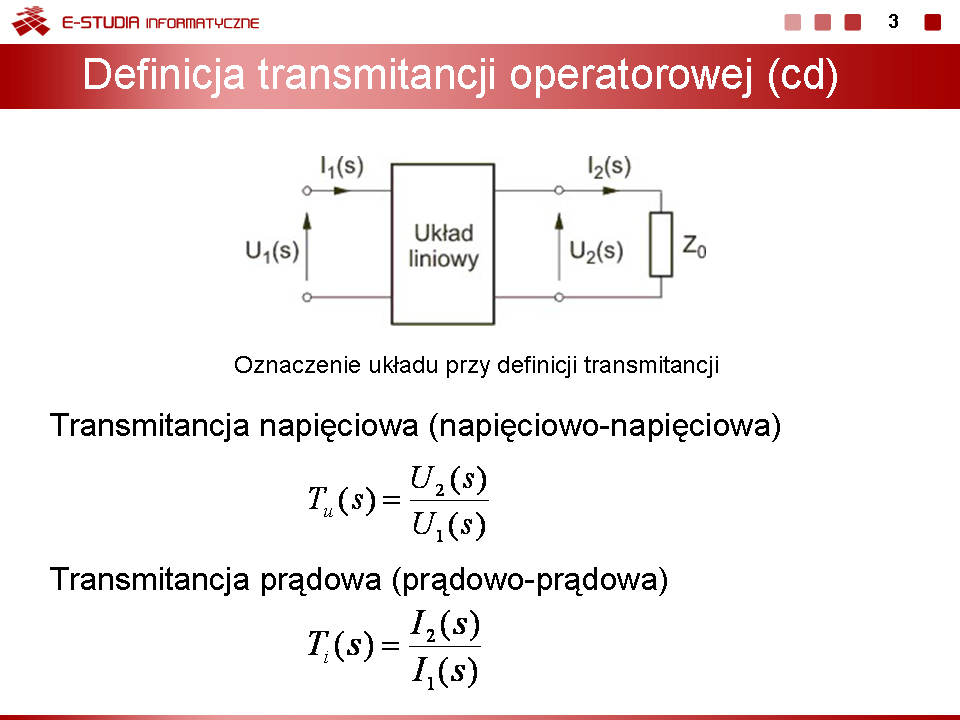
: <math>T_i(s)=\frac{I_2(s)}{I_1(s)}</math> | : <math>T_i(s)=\frac{I_2(s)}{I_1(s)}</math> | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd4.png]] | |||
|valign="top"|'''Transmitancja napięciowo-prądowa''' | |||
Transmitancja napięciowo-prądowa przyjmuje napięcie na dowolnym elemencie obwodu jako sygnał wyjściowy Y(s). Sygnałem wejściowym X(s) jest wymuszenie prądowe. Jest zatem zdefiniowana w postaci | |||
: <math>T_{ui}(s)=\frac{U_2(s)}{I_1(s)}</math> | |||
Napięcie <math>U_2</math> mierzone jest w stanie jałowym <math>(Z_0=\infty)</math> obwodu. | |||
'''Transmitancja prądowo-napięciowa''' | |||
Transmitancję prądowo-napięciową definiuje się jako stosunek prądu wyjściowego do napięcia wejściowego (sygnałem wejściowym X(s) jest napięcie wymuszające a sygnałem wyjściowym Y(s) prąd dowolnego elementu w obwodzie) | |||
: <math>T_{iu}(s)=\frac{I_2(s)}{U_1(s)}</math> | |||
Szczególnym przypadkiem transmitancji napięciowo-prądowej jest impedancja wejściowa układu, w definicji której przyjmuje się, że prąd i napięcie dotyczą tej samej bramy wejściowej. Jej definicja jest przyjmowana w postaci | |||
: <math>Z_{we}(s)=\frac{U_1(s)}{I_1(s)}</math> | |||
Definicja impedancji wejściowej układu zakłada dowolny stan obciążenia <math>Z_0</math>. Należy jednak zwrócić uwagę, że każda zmiana impedancji obciążenia zmienia impedancję wejściową. Stąd definiując impedancję wejściową należy sprecyzować, przy jakim obciążeniu jest ona wyznaczana. | |||
W identyczny sposób można zdefiniować impedancję wyjściową, w której prąd i napięcie dotyczą bramy wyjściowej układu Odwrotność impedancji wejściowej (lub wyjściowej) nazywana jest admitancją wejściową (wyjściową), która może być zinterpretowana jako szczególny przypadek transmitancji prądowo-napięciowej. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd5.png]] | |||
|valign="top"|'''Transmitancja operatorowa obwodów RLC''' | |||
Przy wyznaczaniu transmitancji operatorowej obwodu zawierającego rezystancje, indukcyjności, indukcyjności sprzężone i pojemności wykorzystuje się model operatorowy poszczególnych elementów R, L, C i M wprowadzony w lekcji poprzedniej. Przy założeniu zerowych warunków początkowych dla indukcyjności i pojemności modele tych elementów nie zawierają źródeł a jedynie impedancje operatorowe Z(s). Zestaw impedancji operatorowych dla elementów pasywnych przedstawiono na slajdzie 5. | |||
Dla obwodów pasywnych zawierających elementy R, L, C i M obliczenie transmitancji operatorowej polega na zastąpieniu elementu rzeczywistego poprzez ich impedancje operatorowe a następnie wykorzystując dowolną metodę analizy (metoda praw Kirchhoffa, węzłowa, oczkowa, Thevenina, Nortona) należy wyznaczyć odpowiedź operatorową w funkcji wymuszenia. Wobec liniowości obwodu każda jego odpowiedź (dowolny prąd i dowolne napięcie) jest liniową funkcją wymuszenia. Obliczając transmitancję dzieli się odpowiedź przez wymuszenie, w wyniku czego zmienna będąca wymuszeniem ulega redukcji i w efekcie transmitancja zależy wyłącznie od parametrów RLC obwodu oraz źródeł sterowanych, będąc jednocześnie funkcją zmiennej zespolonej s. Metodę wyznaczania transmitancji operatorowej zilustrujemy na przykładzie obwodu LC przedstawionego na slajdzie 8. | |||
W ogólnym przypadku obwodu elektrycznego liniowego zawierającego rezystory, cewki i kondensatory oraz źródła sterowane dowolna transmitancja operatorowa ma postać funkcji wymiernej o stopniu licznika równym m i stopniu mianownika równym n | |||
<math>T(s)=\frac{L(s)}{M(s)}=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0}</math> | |||
Współczynniki <math>a_i</math> mianownika oraz <math>b_i</math> licznika są funkcjami parametrów elementów obwodu i dla ich konkretnych wartości przyjmują wartości rzeczywiste. Najwyższy stopień wielomianu jest równy (w szczególnych przypadkach mniejszy) liczbie elementów reaktancyjnych (cewek i kondensatorów) obwodu. Najczęściej w obwodach występujących w praktyce stopień mianownika jest nie mniejszy niż stopień licznika. | |||
Pojęcie impedancji operatorowej jest uogólnieniem impedancji zespolonej elementów stosowanej w metodzie symbolicznej przy analizie stanów ustalonych w obwodzie zawierającym wymuszenia sinusoidalne. Łatwo pokazać to zakładając <math>s=j\omega</math> we wzorach określających odpowiednie impedancje operatorowe. Dla elementów indukcyjnych i pojemnościowych przy założeniu <math>s=j\omega</math> otrzymuje się następujące zależności | |||
: <math>Z_L(s)|_{s=j\omega}=j\omega L=Z_L(j\omega)</math> | |||
: <math>Z_M(s)|_{s=j\omega}=\pm j\omega M=Z_M(j\omega)</math> | |||
: <math>Z_C(s)|_{s=j\omega}=\frac{1}{j\omega C}=Z_C(j\omega)</math> | |||
Impedancje <math>Z(j\omega)</math> reprezentują impedancje symboliczne elementów RLC, obowiązujące w analizie stanów ustalonych przy wymuszeniach sinusoidalnych. Założenie <math>s=j\omega</math> upraszcza zatem opis obwodu w stanie nieustalonym do opisu obwodu w stanie ustalonym przy założeniu wymuszenia sinusoidalnego. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 15:08, 1 sie 2006

|
Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów |