|
|
| Linia 121: |
Linia 121: |
| {| border="0" cellpadding="4" width="125%" | | {| border="0" cellpadding="4" width="125%" |
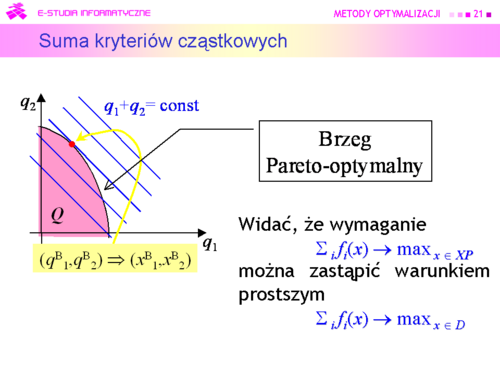
| |width="500px" valign="top"|[[Grafika:MO_M10_Slajd21.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M10_Slajd21.png|thumb|500px]] |
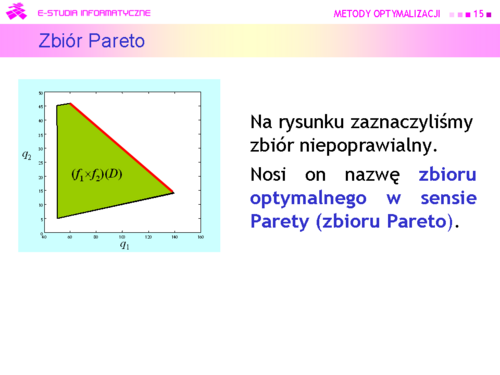
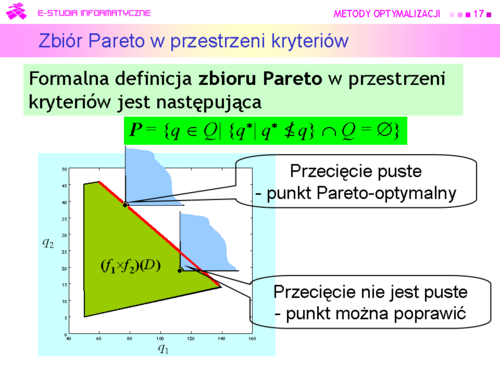
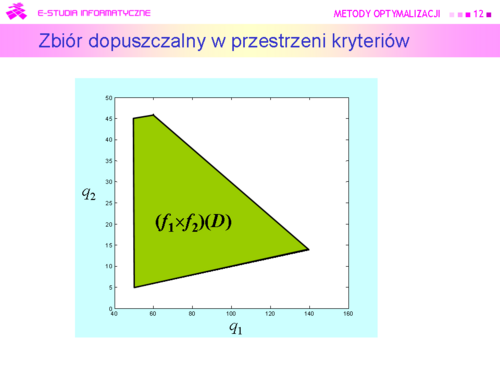
| |valign="top"|Ponieważ zbiór Pareto w przestrzeni kryteriów w zadaniu decyzyjnym pana X jest następujący<br><math> \boldsymbol{P} = \{(q_1,q_2) \in [60,140] \times [14,46] |\, q_2 =70 - {2 \over 5}q_1 \}</math>, | | |valign="top"|Ponieważ zbiór Pareto w przestrzeni kryteriów w zadaniu decyzyjnym pana X jest następujący<br><math>\boldsymbol{P} = \{(q_1,q_2) \in [60,140] \times [14,46] |\, q_2 =70 - {2 \over 5}q_1 \}</math>, |
| to '''podejście utylitarianistyczne''' oparte na maksymalizacji sumy<br><math>(q_1,q_2) \mapsto u(q_1,q_2) = q_1 + q_2</math><br> | | to '''podejście utylitarianistyczne''' oparte na maksymalizacji sumy<br><math>(q_1,q_2) \mapsto u(q_1,q_2) = q_1 + q_2</math><br> |
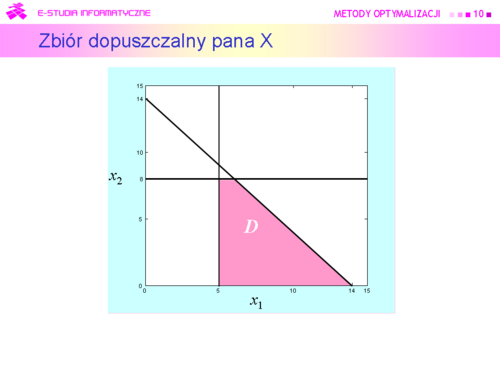
| jako rozwiązanie da <math>(q_1^{\mathrm B},q_2^{\mathrm B})= (140,14)</math> oraz decyzję <math>(x_1^{\mathrm B},x_2^{\mathrm B})=(14,0)</math> – '''tylko pracować'''. (Dobrze jest wykonać stosowny rysunek.) | | jako rozwiązanie da <math>(q_1^{\mathrm B},q_2^{\mathrm B})= (140,14)</math> oraz decyzję <math>(x_1^{\mathrm B},x_2^{\mathrm B})=(14,0)</math> – '''tylko pracować'''. (Dobrze jest wykonać stosowny rysunek.) |