Analiza matematyczna 1/Ćwiczenia 2: Funkcje elementarne: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „.</math>” na „</math>.” |
m Zastępowanie tekstu – „,</math>” na „</math>,” |
||
| Linia 28: | Linia 28: | ||
funkcją odwrotną do <math> f</math>. A więc funkcją odwrotną do <math> f</math> jest | funkcją odwrotną do <math> f</math>. A więc funkcją odwrotną do <math> f</math> jest | ||
<math> f</math>.<br> | <math> f</math>.<br> | ||
c) Funkcją odwrotną do <math> f</math> jest <math> f</math>, więc <math> f\circ f =\mathrm{id}\ | c) Funkcją odwrotną do <math> f</math> jest <math> f</math>, więc <math> f\circ f =\mathrm{id}\</math>,, gdzie | ||
<math> \mathrm{id}\,: x\mapsto x</math> oznacza odwzorowanie identycznościowe. Wobec | <math> \mathrm{id}\,: x\mapsto x</math> oznacza odwzorowanie identycznościowe. Wobec | ||
tego <math> f^3 =(f\circ f)\circ f=\mathrm{id}\,\circ f=f</math>. Podobnie <math> f^4=(f\circ | tego <math> f^3 =(f\circ f)\circ f=\mathrm{id}\,\circ f=f</math>. Podobnie <math> f^4=(f\circ | ||
f)\circ (f\circ f)=\mathrm{id}\, \circ \mathrm{id}\, =\mathrm{id}\ | f)\circ (f\circ f)=\mathrm{id}\, \circ \mathrm{id}\, =\mathrm{id}\</math>,. Spostrzegamy, że: | ||
<center><math> f^n | <center><math> f^n | ||
| Linia 81: | Linia 81: | ||
homografią odwrotną do <math>f</math> jest ta sama funkcja.<br> | homografią odwrotną do <math>f</math> jest ta sama funkcja.<br> | ||
c) Skoro <math>f^{-1}=f</math>, więc - podobnie jak w [[#cwiczenie_2_1|ćwiczeniu 2.1.]] - złożenie | c) Skoro <math>f^{-1}=f</math>, więc - podobnie jak w [[#cwiczenie_2_1|ćwiczeniu 2.1.]] - złożenie | ||
<math>f\circ f=\mathrm{id}\ | <math>f\circ f=\mathrm{id}\</math>,, <math>f^4=(f\circ f)\circ (f\circ f)=\mathrm{id}\, \circ \mathrm{id}\, =\mathrm{id}\</math>,. | ||
Spostrzegamy, że: | Spostrzegamy, że: | ||
| Linia 137: | Linia 137: | ||
redukcyjnego: <math> \cos x=\sin\left(\frac{\pi}{2}-x\right)</math>, otrzymujemy | redukcyjnego: <math> \cos x=\sin\left(\frac{\pi}{2}-x\right)</math>, otrzymujemy | ||
<center><math> \arcsin(\cos | <center><math> \arcsin(\cos | ||
x)=\arcsin\left(\sin\left(\frac{\pi}{2}-x\right)\right)=\frac{\pi}{2}-x | x)=\arcsin\left(\sin\left(\frac{\pi}{2}-x\right)\right)=\frac{\pi}{2}-x</math>,</center> | ||
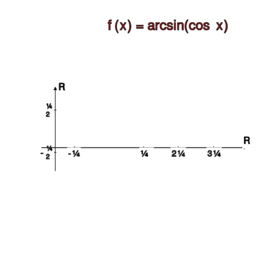
dla <math> 0\leq x\leq \pi</math>. Wobec parzystości rozważanej funkcji mamy dla <math> -\pi\leq x\leq\pi</math> równość <center><math> \arcsin(\cos x)=\frac{\pi}{2}-|x|</math>.</center> <br> | dla <math> 0\leq x\leq \pi</math>. Wobec parzystości rozważanej funkcji mamy dla <math> -\pi\leq x\leq\pi</math> równość <center><math> \arcsin(\cos x)=\frac{\pi}{2}-|x|</math>.</center> <br> | ||
| Linia 194: | Linia 194: | ||
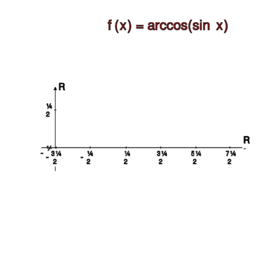
Podobnie dostajemy równość: <math> \cos(\arcsin x)=\sqrt{1-x^2}</math> dla <math> -1\leq x\leq 1</math>.<br> | Podobnie dostajemy równość: <math> \cos(\arcsin x)=\sqrt{1-x^2}</math> dla <math> -1\leq x\leq 1</math>.<br> | ||
c) Funkcja <math> x\mapsto \mathrm{arctg}\,(\mathrm{ctg}\, x)</math> jest nieparzysta, gdyż jest złożeniem dwóch funkcji nieparzystych: <math> x\mapsto \mathrm{ctg}\, x</math> oraz <math> u\mapsto \mathrm{arctg}\, u</math>. Jest okresowa o okresie <math> \pi</math> wystarczy więc rozważyć ją np. na przedziale <math> 0<x<\pi</math>. Ze wzoru redukcyjnego mamy <math> \mathrm{ctg}\, x=\mathrm{tg}\,\left(\frac{\pi}{2}-x\right) | c) Funkcja <math> x\mapsto \mathrm{arctg}\,(\mathrm{ctg}\, x)</math> jest nieparzysta, gdyż jest złożeniem dwóch funkcji nieparzystych: <math> x\mapsto \mathrm{ctg}\, x</math> oraz <math> u\mapsto \mathrm{arctg}\, u</math>. Jest okresowa o okresie <math> \pi</math> wystarczy więc rozważyć ją np. na przedziale <math> 0<x<\pi</math>. Ze wzoru redukcyjnego mamy <math> \mathrm{ctg}\, x=\mathrm{tg}\,\left(\frac{\pi}{2}-x\right)</math>, stąd | ||
<center> | <center> | ||
| Linia 226: | Linia 226: | ||
Wykazać, że dla dowolnych liczb <math> x</math>, <math> y</math> | Wykazać, że dla dowolnych liczb <math> x</math>, <math> y</math> | ||
zachodzą równości:<br> | zachodzą równości:<br> | ||
a) <math> \cosh(x+y)=\cosh x \cosh y+\sinh x\sinh y | a) <math> \cosh(x+y)=\cosh x \cosh y+\sinh x\sinh y</math>,<br> | ||
b) <math> \sinh(x+y)=\sinh x\cosh y+\cosh x \sinh y</math>. | b) <math> \sinh(x+y)=\sinh x\cosh y+\cosh x \sinh y</math>. | ||
}}</span> | }}</span> | ||
Wersja z 09:26, 5 wrz 2023
Funkcje elementarne
Ćwiczenie 2.1.
Dana jest funkcja afiniczna . Wyznaczyć:
a) odwrotność tej funkcji,
b) funkcję odwrotną do ,
c) złożenie , , , .
d) Czy istnieje malejąca funkcja
afiniczna taka, że ?
Ćwiczenie 2.2.
Dana jest homografia
. Wyznaczyć:
a) odwrotność tej homografii,
b) homografię odwrotną,
c) złożenie , , oraz .
d) Czy istnieje homografia taka, że
?
Ćwiczenie 2.3.
Wyrazić w prostszej postaci:
a) , ,
b) , ,
c) , ,
d) , ,
e) , .
Ćwiczenie 2.4.
Wykazać, że dla dowolnych liczb ,
zachodzą równości:
a) ,
b) .
Ćwiczenie 2.5.
a) Niech dla .. Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla ..
Ćwiczenie 2.6.
a) Niech dla .. Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla ..
c) Wykazać, że dla dowolnej liczby . istnieje
wielomian taki, że oraz są restrykcjami -
odpowiednio do przedziałów oraz -
wielomianu .