Analiza matematyczna 2/Ćwiczenia 12: Całka krzwoliniowa. Twierdzenie Greena: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „\displaystyle” na „” |
m Zastępowanie tekstu – „.</math>” na „</math>.” |
||
| Linia 75: | Linia 75: | ||
<math>B_2</math> będzie odcinkiem łączącym <math>(1,-1)</math> z <math>(1,1)</math>;<br> | <math>B_2</math> będzie odcinkiem łączącym <math>(1,-1)</math> z <math>(1,1)</math>;<br> | ||
<math>B_3</math> będzie odcinkiem łączącym <math>(1,1)</math> z <math>(-1,1)</math>;<br> | <math>B_3</math> będzie odcinkiem łączącym <math>(1,1)</math> z <math>(-1,1)</math>;<br> | ||
<math>B_4</math> będzie odcinkiem łączącym <math>(-1,1)</math> z <math>(-1,-1) | <math>B_4</math> będzie odcinkiem łączącym <math>(-1,1)</math> z <math>(-1,-1)</math>. | ||
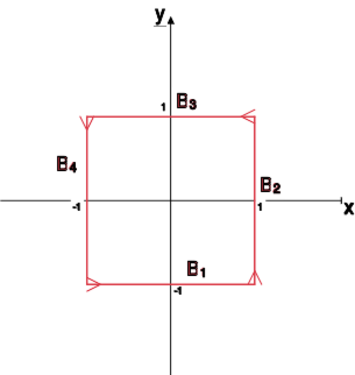
[[File:Am2.12.5.svg|375x375px|thumb|left|Orientacja krzywej z ćwiczenia 12.2.]] | [[File:Am2.12.5.svg|375x375px|thumb|left|Orientacja krzywej z ćwiczenia 12.2.]] | ||
Zwróćmy uwagę na to, że musimy tak dobrać parametryzację | Zwróćmy uwagę na to, że musimy tak dobrać parametryzację | ||
| Linia 114: | Linia 114: | ||
'''Sposób II.''' | '''Sposób II.''' | ||
Skorzystajmy z twierdzenia Greena. Oznaczmy przez <math>D</math> | Skorzystajmy z twierdzenia Greena. Oznaczmy przez <math>D</math> | ||
wnętrze kwadratu ograniczonego krzywą <math>K | wnętrze kwadratu ograniczonego krzywą <math>K</math>. | ||
Policzmy najpierw | Policzmy najpierw | ||
| Linia 152: | Linia 152: | ||
Policzyć pracę | Policzyć pracę | ||
potrzebną do przesunięcia punktu materialnego wzdłuż krzywej <math>K</math> | potrzebną do przesunięcia punktu materialnego wzdłuż krzywej <math>K</math> | ||
łączącej punkt <math>(0,0)</math> z punktem <math>(1,1),</math> danej wzorem <math>y=x^{20} | łączącej punkt <math>(0,0)</math> z punktem <math>(1,1),</math> danej wzorem <math>y=x^{20}</math>. | ||
}} | }} | ||
| Linia 161: | Linia 161: | ||
potencjalnym, zatem obliczana praca nie zależy od drogi. Można | potencjalnym, zatem obliczana praca nie zależy od drogi. Można | ||
więc wybrać dowolną drogę całkowania, najlepiej odcinek łączący | więc wybrać dowolną drogę całkowania, najlepiej odcinek łączący | ||
punkt <math>(0,0)</math> z punktem <math>(1,1) | punkt <math>(0,0)</math> z punktem <math>(1,1)</math>. | ||
</div></div> | </div></div> | ||
| Linia 266: | Linia 266: | ||
gdzie <math>g</math> jest pewną | gdzie <math>g</math> jest pewną | ||
różniczkowalną funkcją zmiennej <math>y | różniczkowalną funkcją zmiennej <math>y</math>. (Dla sprawdzenia można | ||
policzyć pochodną po <math>x</math> z obu stron tej równości). Aby znaleźć | policzyć pochodną po <math>x</math> z obu stron tej równości). Aby znaleźć | ||
<math>g</math>, policzmy pochodną po <math>y</math> | <math>g</math>, policzmy pochodną po <math>y</math> | ||
| Linia 329: | Linia 329: | ||
gdzie <math>K</math> jest okręgiem | gdzie <math>K</math> jest okręgiem | ||
środku w <math>(0,0)</math> i promieniu <math>1 | środku w <math>(0,0)</math> i promieniu <math>1</math>. | ||
}} | }} | ||
| Linia 363: | Linia 363: | ||
gdzie <math>K</math> jest wykresem funkcji | gdzie <math>K</math> jest wykresem funkcji | ||
<math>y=\sin x,</math> dla <math>x\in [0,\pi] | <math>y=\sin x,</math> dla <math>x\in [0,\pi]</math>. | ||
}} | }} | ||
| Linia 369: | Linia 369: | ||
Krzywa <math>K</math> nie jest krzywą zamkniętą, można jednak | Krzywa <math>K</math> nie jest krzywą zamkniętą, można jednak | ||
"dokleić" do niej odcinek <math>[0,\pi]</math> - wtedy krzywa będzie | "dokleić" do niej odcinek <math>[0,\pi]</math> - wtedy krzywa będzie | ||
ograniczać pewien obszar <math>D | ograniczać pewien obszar <math>D</math>. Teraz można skorzystać z | ||
twierdzenia Greena. | twierdzenia Greena. | ||
</div></div> | </div></div> | ||
| Linia 376: | Linia 376: | ||
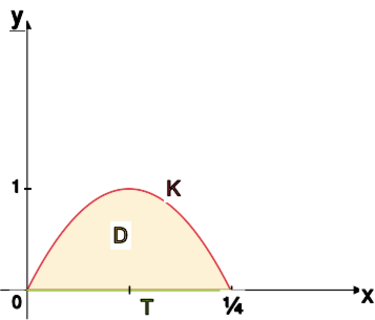
[[File:Am2.12.6.svg|375x375px|thumb|left|Obszar <math>D</math> ograniczony wykresem funkcji <math>\sin</math> oraz osią <math>Ox</math>]] | [[File:Am2.12.6.svg|375x375px|thumb|left|Obszar <math>D</math> ograniczony wykresem funkcji <math>\sin</math> oraz osią <math>Ox</math>]] | ||
Krzywą <math>K</math> oczywiście możemy | Krzywą <math>K</math> oczywiście możemy | ||
sparametryzować <math>x=t, y=\sin t, t\in [0,\pi] | sparametryzować <math>x=t, y=\sin t, t\in [0,\pi]</math>. Licząc całkę, | ||
dostajemy: | dostajemy: | ||
| Linia 392: | Linia 392: | ||
nie jest zamknięta, musimy najpierw "dokleić" do niej inną krzywą, | nie jest zamknięta, musimy najpierw "dokleić" do niej inną krzywą, | ||
tak by razem ograniczały jakiś obszar. Weźmy zatem jako tą | tak by razem ograniczały jakiś obszar. Weźmy zatem jako tą | ||
dodatkową krzywą odcinek <math>T:=[0, \pi] | dodatkową krzywą odcinek <math>T:=[0, \pi]</math>. Obszar ograniczony | ||
odcinkiem i wykresem funkcji <math>\sin x</math> nazwiemy | odcinkiem i wykresem funkcji <math>\sin x</math> nazwiemy | ||
<math>D | <math>D</math>.<br> | ||
Aby zastosować | Aby zastosować | ||
| Linia 400: | Linia 400: | ||
zorientowany dodatnio, a zatem krzywą <math>K</math> będziemy teraz | zorientowany dodatnio, a zatem krzywą <math>K</math> będziemy teraz | ||
przebiegać w kierunku od <math>x=\pi</math> do <math>x=0,</math> przeciwnym do zadanego. | przebiegać w kierunku od <math>x=\pi</math> do <math>x=0,</math> przeciwnym do zadanego. | ||
Brzeg <math>D</math> możemy więc zapisać jako <math>\partial D=-K+T | Brzeg <math>D</math> możemy więc zapisać jako <math>\partial D=-K+T</math>. Mamy zatem: | ||
<center> | <center> | ||
| Linia 473: | Linia 473: | ||
gdzie <math>K</math> jest parabolą | gdzie <math>K</math> jest parabolą | ||
<math>y=-x^2+1</math> pomiędzy punktami <math>(-1,0)</math> a <math>(1,0) | <math>y=-x^2+1</math> pomiędzy punktami <math>(-1,0)</math> a <math>(1,0)</math>. | ||
}} | }} | ||
| Linia 486: | Linia 486: | ||
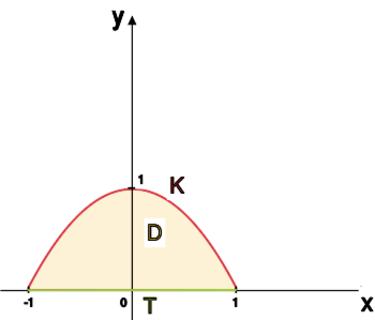
przy pomocy sparametryzowania krzywej będzie trudne. Postaramy sie | przy pomocy sparametryzowania krzywej będzie trudne. Postaramy sie | ||
skorzystać z twierdzenia Greena. Aby dostać krzywą zamkniętą, do | skorzystać z twierdzenia Greena. Aby dostać krzywą zamkniętą, do | ||
krzywej <math>K</math> "doklejamy" odcinek <math>T=[-1,1] | krzywej <math>K</math> "doklejamy" odcinek <math>T=[-1,1]</math>. Otrzymany obszar | ||
oznaczamy przez <math>D | oznaczamy przez <math>D</math>.<br> | ||
Brzeg <math>D</math> ma być zorientowany dodatnio, zatem na krzywej <math>K</math> | Brzeg <math>D</math> ma być zorientowany dodatnio, zatem na krzywej <math>K</math> | ||
musimy wziąć parametryzację dającą orientację przeciwną, | musimy wziąć parametryzację dającą orientację przeciwną, | ||
<math>\partial D=-K+T | <math>\partial D=-K+T</math>. Mamy zatem: | ||
<center> | <center> | ||
| Linia 556: | Linia 556: | ||
[[File:AM2.M12.C.R05.mp4|253x253px|thumb|right|Elipsa]] | [[File:AM2.M12.C.R05.mp4|253x253px|thumb|right|Elipsa]] | ||
Parametryzacja elipsy to <math>x=a\cos t, y=b\sin t, t\in[0,2\pi] | Parametryzacja elipsy to <math>x=a\cos t, y=b\sin t, t\in[0,2\pi]</math>.<br> | ||
</div></div> | </div></div> | ||
| Linia 617: | Linia 617: | ||
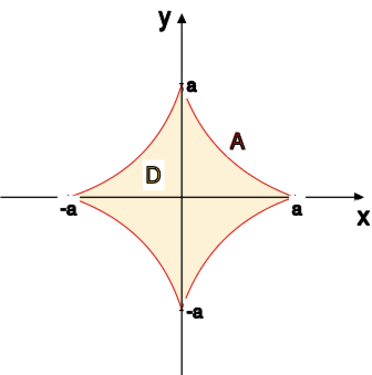
[[File:Am2.12.8.svg|375x375px|thumb|left|Asteroida]] | [[File:Am2.12.8.svg|375x375px|thumb|left|Asteroida]] | ||
Parametryzacja | Parametryzacja | ||
asteroidy to <math>x=a\cos^3t, y=a\sin^3t, t\in [0, 2\pi] | asteroidy to <math>x=a\cos^3t, y=a\sin^3t, t\in [0, 2\pi]</math>.<br> | ||
</div></div> | </div></div> | ||
Wersja z 09:14, 5 wrz 2023
Całka krzywoliniowa. Twierdzenie Greena
Ćwiczenie 12.1.
Policzyć
gdzie jest łukiem cykloidy danej parametrycznie:
Ćwiczenie 12.2.
Policzyć
gdzie jest kwadratem o wierzchołkach w obieganym przeciwnie do ruchu wskazówek zegara.
Ćwiczenie 12.3.
W pewnym polu sił składowe pola wynoszą
Policzyć pracę potrzebną do przesunięcia punktu materialnego wzdłuż krzywej łączącej punkt z punktem danej wzorem .
Ćwiczenie 12.4.
Znaleźć (lub odgadnąć) potencjał dla pola sił z ćwiczenia 12.3.
Ćwiczenie 12.5.
Korzystając z twierdzenia Greena, policzyć
gdzie jest okręgiem środku w i promieniu .
Ćwiczenie 12.6.
Policzyć całkę
gdzie jest wykresem funkcji dla .
Ćwiczenie 12.7.
Policzyć całkę krzywoliniową:
gdzie jest parabolą pomiędzy punktami a .
Ćwiczenie 12.8.
Za pomocą całki krzywoliniowej skierowanej obliczyć pole ograniczone elipsą
gdzie są dane.
Ćwiczenie 12.9.
Za pomocą całki krzywoliniowej skierowanej obliczyć pole ograniczone asteroidą
gdzie jest dane.