Analiza matematyczna 1/Ćwiczenia 2: Funkcje elementarne: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „\displaystyle ” na „” |
|||
| Linia 64: | Linia 64: | ||
f \circ f\circ f\circ f \circ f\circ f\circ f \circ f\circ f\circ | f \circ f\circ f\circ f \circ f\circ f\circ f \circ f\circ f\circ | ||
f </math>.<br> | f </math>.<br> | ||
d) Czy istnieje homografia <math>g: \mathbb{R}\mapsto \mathbb{R}</math> taka, że | d) Czy istnieje homografia <math>g: \mathbb{R} \mapsto \mathbb{R}</math> taka, że | ||
<math>g\circ g =f</math>? | <math>g\circ g = f</math>? | ||
}} | }} | ||
Wersja z 09:03, 28 sie 2023
Funkcje elementarne
Ćwiczenie 2.1.
Dana jest funkcja afiniczna . Wyznaczyć:
a) odwrotność tej funkcji,
b) funkcję odwrotną do ,
c) złożenie , , , .
d) Czy istnieje malejąca funkcja
afiniczna taka, że ?
Ćwiczenie 2.2.
Dana jest homografia
. Wyznaczyć:
a) odwrotność tej homografii,
b) homografię odwrotną,
c) złożenie , , oraz .
d) Czy istnieje homografia taka, że
?
Ćwiczenie 2.3.
Wyrazić w prostszej postaci:
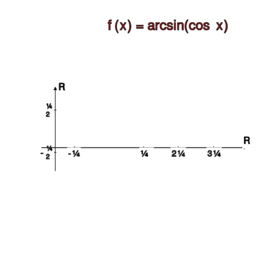
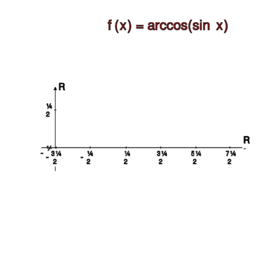
a) , ,
b) , ,
c) , ,
d) , ,
e) , .
Ćwiczenie 2.4.
Wykazać, że dla dowolnych liczb ,
zachodzą równości:
a)
b)
Ćwiczenie 2.5.
a) Niech dla . Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla .
Ćwiczenie 2.6.
a) Niech dla . Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla .
c) Wykazać, że dla dowolnej liczby istnieje
wielomian taki, że oraz są restrykcjami -
odpowiednio do przedziałów oraz -
wielomianu .