Analiza matematyczna 1/Ćwiczenia 2: Funkcje elementarne: Różnice pomiędzy wersjami
| Linia 57: | Linia 57: | ||
Dana jest homografia | Dana jest homografia | ||
<math> | <math>f(x)=\frac{x+1}{x-1}</math>. Wyznaczyć:<br> | ||
a) odwrotność tej homografii,<br> | a) odwrotność tej homografii,<br> | ||
b) homografię odwrotną,<br> | b) homografię odwrotną,<br> | ||
c) złożenie <math> f^2 = f \circ f</math>, <math> f^3 = f\circ | c) złożenie <math>f^2 = f \circ f</math>, <math>f^3 = f\circ | ||
f \circ f</math>, <math>f^4 = f\circ f \circ f\circ f</math> oraz <math>f^{11} = f\circ | f \circ f</math>, <math>f^4 = f\circ f \circ f\circ f</math> oraz <math>f^{11} = f\circ | ||
f \circ f\circ f\circ f \circ f\circ f\circ f \circ f\circ f\circ | f \circ f\circ f\circ f \circ f\circ f\circ f \circ f\circ f\circ | ||
| Linia 72: | Linia 72: | ||
d) Niech <math>g(x)=\frac{ax +b}{cx +d}</math>. | d) Niech <math>g(x)=\frac{ax +b}{cx +d}</math>. | ||
Zauważyć, że można przyjąć, że <math>c=1</math> (dlaczego?). Jakie równania | Zauważyć, że można przyjąć, że <math>c=1</math> (dlaczego?). Jakie równania | ||
muszą spełniać współczynniki <math> \ a, \ b, \ d</math>, aby <math> | muszą spełniać współczynniki <math>\ a,\ b,\ d</math>, aby <math>g\circ g=f</math>? | ||
</div></div> | </div></div> | ||
| Linia 78: | Linia 78: | ||
a) Odwrotnością danej homografii jest | a) Odwrotnością danej homografii jest | ||
<math>x\mapsto\frac{1}{f(x)}=\frac{x-1}{x+1}</math>.<br> | <math>x\mapsto\frac{1}{f(x)}=\frac{x-1}{x+1}</math>.<br> | ||
b) Homografię odwrotną do <math> | b) Homografię odwrotną do <math>f</math> otrzymamy, wyznaczając <math>x</math> z | ||
równania <math> | równania <math>y=\frac{x+1}{x-1}</math>. Stąd | ||
<math> | <math>x=\frac{y+1}{y-1}</math>, czyli | ||
homografią odwrotną do <math> | homografią odwrotną do <math>f</math> jest ta sama funkcja.<br> | ||
c) Skoro <math> | c) Skoro <math>f^{-1}=f</math>, więc - podobnie jak w [[#cwiczenie_2_1|ćwiczeniu 2.1.]] - złożenie | ||
<math> | <math>f\circ f=\mathrm{id}\,</math>, <math>f^4=(f\circ f)\circ (f\circ f)=\mathrm{id}\, \circ \mathrm{id}\, =\mathrm{id}\,</math>. | ||
Spostrzegamy, że: | Spostrzegamy, że: | ||
<center><math> | <center><math>f^n | ||
= | = | ||
\left\{ \begin{array}{ll} f, &\text{ jeśli }n \text{ jest liczbą nieparzystą},\\ | \left\{ \begin{array}{ll} f, &\text{ jeśli }n \text{ jest liczbą nieparzystą},\\ | ||
| Linia 92: | Linia 92: | ||
</math></center> | </math></center> | ||
wobec tego <math> | wobec tego <math>f^3=f</math>, <math>f^{11}=f</math>.<br> | ||
d) Niech <math> | d) Niech <math>g(x)=\frac{ax+b}{cx+d}</math>. Współczynnik <math>c\neq 0</math>, gdyż | ||
w przeciwnym przypadku funkcja <math> | w przeciwnym przypadku funkcja <math>g</math> byłaby afiniczna i złożenie | ||
<math> | <math>g\circ g</math> byłoby funkcją afiniczną, co nie jest możliwe. Skoro <math>c\neq 0</math> | ||
możemy podzielić licznik i mianownik rozważanego ułamka przez stałą <math> | możemy podzielić licznik i mianownik rozważanego ułamka przez stałą <math>c</math> | ||
i przyjąć, że <math> | i przyjąć, że <math>c=1</math> to znaczy: <math>g(x)=\frac{ax+b}{x+d}</math>. Wobec tego | ||
<center><math> | <center><math>\begin{align} (g\circ g)(x)=&g(g(x)) | ||
=\frac{ag(x)+b}{g(x)+d}\\=&\frac{a\frac{ax+b}{x+d}+b}{\frac{ax+b}{x+d}+d} | =\frac{ag(x)+b}{g(x)+d}\\=&\frac{a\frac{ax+b}{x+d}+b}{\frac{ax+b}{x+d}+d} | ||
=\frac{a(ax+b)+b(x+d)}{ax+b+d(x+d)}=\frac{(a^2+b)x+(ab+bd)}{(a+d)x+(b+d^2)}.\end{align} | =\frac{a(ax+b)+b(x+d)}{ax+b+d(x+d)}=\frac{(a^2+b)x+(ab+bd)}{(a+d)x+(b+d^2)}.\end{align} | ||
</math></center> | </math></center> | ||
Równość <math> | Równość <math>g\circ g=f</math> zachodziłaby, gdyby odpowiednie współczynniki homografii <math>g\circ g</math> oraz <math>f</math> były równe, | ||
<center><math> | <center><math>0\neq a^2+b=b(a+d)=a+d=-(b+d^2).</math></center> | ||
Ale jest to niemożliwe, gdyż z równości <math> | Ale jest to niemożliwe, gdyż z równości <math>b(a+d)=a+d</math> wynika, że <math>b=1</math>, co pociąga za sobą w konsekwencji nierówność: <math>1\leq a^2 +1=a^2 | ||
+b=-(b+d^2)=-(1+d^2)\leq -1</math>, która jest fałszywa. Nie ma więc takiej homografii <math> | +b=-(b+d^2)=-(1+d^2)\leq -1</math>, która jest fałszywa. Nie ma więc takiej homografii <math>g:\mathbb{R}\mapsto\mathbb{R}</math>, aby <math>g\circ g=f</math>. | ||
</div></div> | </div></div> | ||
Wersja z 20:15, 27 sie 2023
Funkcje elementarne
Ćwiczenie 2.1.
Dana jest funkcja afiniczna . Wyznaczyć:
a) odwrotność tej funkcji,
b) funkcję odwrotną do ,
c) złożenie , , , .
d) Czy istnieje malejąca funkcja
afiniczna taka, że ?
Ćwiczenie 2.2.
Dana jest homografia
. Wyznaczyć:
a) odwrotność tej homografii,
b) homografię odwrotną,
c) złożenie , , oraz .
d) Czy istnieje homografia taka, że
?
Ćwiczenie 2.3.
Wyrazić w prostszej postaci:
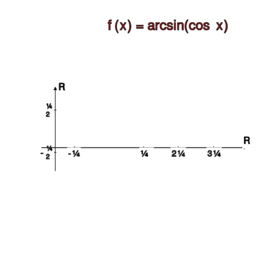
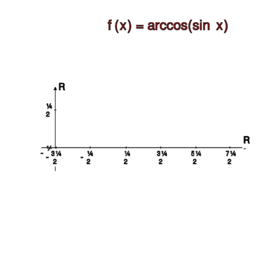
a) , ,
b) , ,
c) , ,
d) , ,
e) , .
Ćwiczenie 2.4.
Wykazać, że dla dowolnych liczb ,
zachodzą równości:
a)
b)
Ćwiczenie 2.5.
a) Niech dla . Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla .
Ćwiczenie 2.6.
a) Niech dla . Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla .
c) Wykazać, że dla dowolnej liczby istnieje
wielomian taki, że oraz są restrykcjami -
odpowiednio do przedziałów oraz -
wielomianu .