Analiza matematyczna 1/Ćwiczenia 2: Funkcje elementarne: Różnice pomiędzy wersjami
m Zastępowanie tekstu - "<div class="thumb t(.*)"><div style="width:(.*);"> <flash>file=(.*)\.swf\|width=(.*)\|height=(.*)<\/flash> <div\.thumbcaption>(.*)<\/div> <\/div><\/div>" na "$4x$5px|thumb|$1|$6" |
|||
| Linia 60: | Linia 60: | ||
a) odwrotność tej homografii,<br> | a) odwrotność tej homografii,<br> | ||
b) homografię odwrotną,<br> | b) homografię odwrotną,<br> | ||
c) złożenie <math> | c) złożenie <math> f^2 = f \circ f</math>, <math> f^3 = f\circ | ||
f \circ f</math>, <math> | f \circ f</math>, <math>f^4 = f\circ f \circ f\circ f</math> oraz <math>f^{11} = f\circ | ||
f \circ f\circ f\circ f \circ f\circ f\circ f \circ f\circ f\circ | f \circ f\circ f\circ f \circ f\circ f\circ f \circ f\circ f\circ | ||
f </math>.<br> | f </math>.<br> | ||
d) Czy istnieje homografia <math> | d) Czy istnieje homografia <math>g: \mathbb{R}\mapsto \mathbb{R}</math> taka, że | ||
<math> | <math>g\circ g =f</math>? | ||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
a), b) c) Zastosować wskazówki do [[#cwiczenie_2_1|ćwiczenia 2.1.]]<br> | a), b) c) Zastosować wskazówki do [[#cwiczenie_2_1|ćwiczenia 2.1.]]<br> | ||
d) Niech <math> | d) Niech <math>g(x)=\frac{ax +b}{cx +d}</math>. | ||
Zauważyć, że można przyjąć, że <math> | Zauważyć, że można przyjąć, że <math>c=1</math> (dlaczego?). Jakie równania | ||
muszą spełniać współczynniki <math> \ | muszą spełniać współczynniki <math> \ a, \ b, \ d</math>, aby <math> \displaystyle g\circ g=f</math>? | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
a) Odwrotnością danej homografii jest | a) Odwrotnością danej homografii jest | ||
<math> | <math>x\mapsto\frac{1}{f(x)}=\frac{x-1}{x+1}</math>.<br> | ||
b) Homografię odwrotną do <math> \displaystyle f</math> otrzymamy, wyznaczając <math> \displaystyle x</math> z | b) Homografię odwrotną do <math> \displaystyle f</math> otrzymamy, wyznaczając <math> \displaystyle x</math> z | ||
równania <math> \displaystyle y=\frac{x+1}{x-1}</math>. Stąd | równania <math> \displaystyle y=\frac{x+1}{x-1}</math>. Stąd | ||
Wersja z 21:41, 21 sie 2023
Funkcje elementarne
Ćwiczenie 2.1.
Dana jest funkcja afiniczna . Wyznaczyć:
a) odwrotność tej funkcji,
b) funkcję odwrotną do ,
c) złożenie , , , .
d) Czy istnieje malejąca funkcja
afiniczna taka, że ?
Ćwiczenie 2.2.
Dana jest homografia
. Wyznaczyć:
a) odwrotność tej homografii,
b) homografię odwrotną,
c) złożenie , , oraz .
d) Czy istnieje homografia taka, że
?
Ćwiczenie 2.3.
Wyrazić w prostszej postaci:
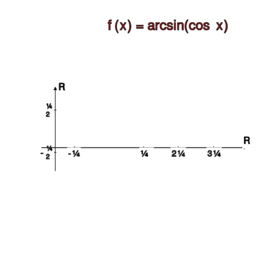
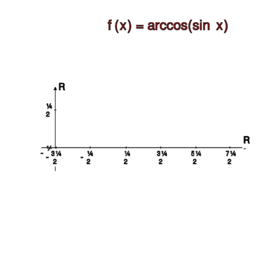
a) , ,
b) , ,
c) , ,
d) , ,
e) , .
Ćwiczenie 2.4.
Wykazać, że dla dowolnych liczb ,
zachodzą równości:
a)
b)
Ćwiczenie 2.5.
a) Niech dla . Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla .
Ćwiczenie 2.6.
a) Niech dla . Wykaż, że , oraz
dla .
b) Wykazać, że funkcja jest wielomianem
zmiennej , dla .
c) Wykazać, że dla dowolnej liczby istnieje
wielomian taki, że oraz są restrykcjami -
odpowiednio do przedziałów oraz -
wielomianu .