PEE Moduł 13: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 71: | Linia 71: | ||
<math>\displaystyle r_F\,</math> - rezystancja dynamiczna diody. | <math>\displaystyle r_F\,</math> - rezystancja dynamiczna diody. | ||
Definicję rezystancji dynamicznej diody przedstawiono na slajdzie. | |||
|} | |} | ||
| Linia 78: | Linia 80: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd7.png|thumb|500px]] | ||
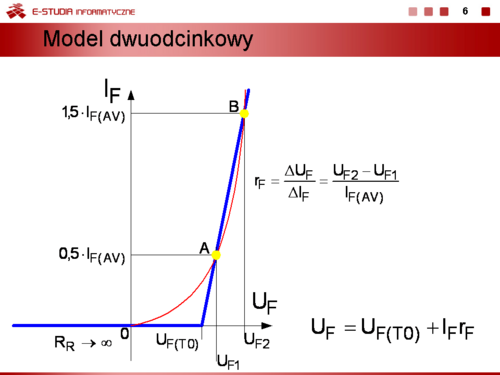
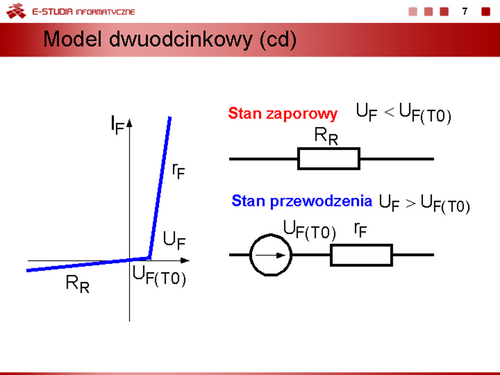
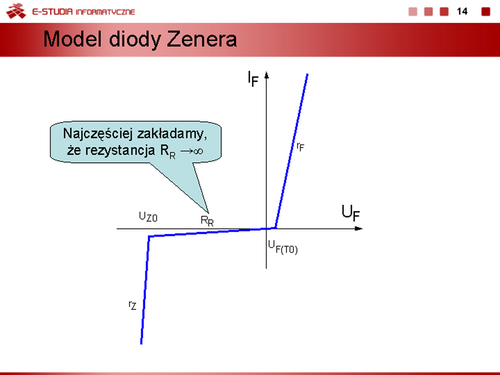
|valign="top"|Jeżeli trzeba uwzględnić wsteczny prąd diody modelujemy charakterystykę w sposób przedstawiony na slajdzie 7. W stanie zaporowym dioda jest reprezentowana przez liniowy rezystor <math>R_R\,</math>, a w stanie przewodzenia przez szeregowy obwód składający się ze źródła napięcia modelującego napięcie progu załączenia diody i rezystancji dynamicznej <math>r_F\,</math>. | |valign="top"|Jeżeli trzeba uwzględnić wsteczny prąd diody modelujemy charakterystykę w sposób przedstawiony na slajdzie 7. W stanie zaporowym dioda jest reprezentowana przez liniowy rezystor <math>R_R\,</math>, a w stanie przewodzenia przez szeregowy obwód składający się ze źródła napięcia modelującego napięcie progu załączenia diody i rezystancji dynamicznej <math>r_F\,</math>. Zatem dla napięć <math>U_F < U_{F(T0)} napięcie na diodzie można wyznaczyć z zależności <math>U_R = I_R\cdot R_R</math>, a wstanie przewodzenia napięcie <math>U_F\,</math> jest opisane wzorem dla modelu dwuodcinkowego. | ||
|} | |} | ||
| Linia 86: | Linia 88: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd8.png|thumb|500px]] | ||
|valign="top"|Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym <math>\displaystyle R_R \to \infty</math>. | |valign="top"|Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym <math>\displaystyle R_R \to \infty</math>. W stanie przewodzenia nadal obowiązuje wzór dla modelu dwuodcinkowego. | ||
|} | |} | ||
| Linia 93: | Linia 95: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
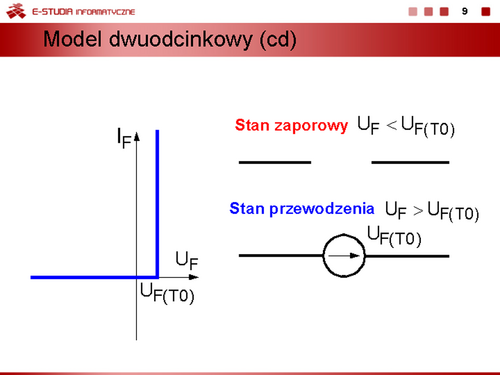
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd9.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd9.png|thumb|500px]] | ||
|valign="top"|Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. | |valign="top"|Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. Oznacza to, że rezystancja dynamiczna diody jest równa zeru. | ||
|} | |} | ||
| Linia 133: | Linia 135: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M13_Slajd12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M13_Slajd12.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|W ogólnym wypadku prąd nasycenia <math>\displaystyle I_S\,</math> zależy od temperatury złącza zgodnie z zależnością | ||
<math>\displaystyle I_S=C\cdot T^3 \cdot e^{\displaystyle\frac{-E_{G0}}{U_T}}</math> | <math>\displaystyle I_S=C\cdot T^3 \cdot e^{\displaystyle\frac{-E_{G0}}{U_T}}</math> | ||
| Linia 157: | Linia 159: | ||
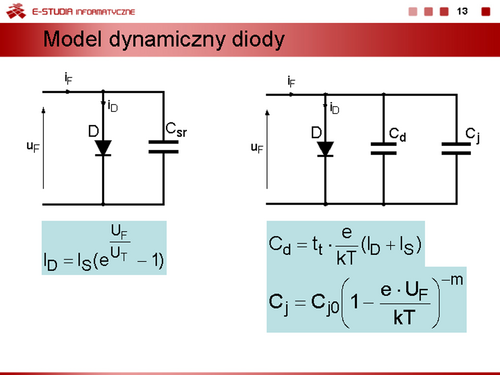
gdzie <math>t_t\,</math> – czas przelotu. | gdzie <math>t_t\,</math> – czas przelotu. | ||
<math>\displaystyle C_j=C_{j0}\left(1-\frac{e\cdot U_F}{kT} \right)^{-m}</math> , | <math>\displaystyle C_j=C_{j0}\left(1-\frac{U_R}{U_D} \right)^{-m}=C_{j0}\left(1-\frac{e\cdot U_F}{kT} \right)^{-m}</math> , | ||
gdzie <math>C_{j0}\,</math> pojemność złącza przy zerowym napięciu polaryzacji, <math>m = 0,5\,</math> dla złącza skokowego, <math>m = 0,333\,</math> dla złącza liniowego. | gdzie <math>C_{j0}\,</math> pojemność złącza przy zerowym napięciu polaryzacji, <math>m = 0,5\,</math> dla złącza skokowego, <math>m = 0,333\,</math> dla złącza liniowego, <math>U_R\,</math> napięcie wsteczne diody, <math>U_D\,</math> potencjał dyfuzyjny złącza. | ||
Pojemność złączową można pominąć, gdy spełniony jest warunek <math>I_D >> I_S</math>. | Pojemność złączową można pominąć, gdy spełniony jest warunek <math>I_D >> I_S</math>. | ||
| Linia 166: | Linia 168: | ||
<math>\displaystyle I_D=I_S \bigg(e^{\displaystyle \frac{U_F}{U_T}}-1\bigg)</math> | <math>\displaystyle I_D=I_S \bigg(e^{\displaystyle \frac{U_F}{U_T}}-1\bigg)</math> | ||
'''Przykład 1''' | |||
Dioda jest w stanie przewodzenia. Prąd <math>I_D = 3 mA</math>, temperatura złącza 300 K. Jaka jest konduktancja dynamiczna diody <math>g_D\,</math> oraz pojemność dyfuzyjna złącza <math>C_d\,</math>, jeżeli czas przelotu (stała czasowa) <math>t_t = 5\, ns</math>. | |||
'''Rozwiązanie:''' | |||
Konduktancję diody można wyznaczyć z zależności: | |||
<math>\displaystyle g_D=\frac{1}{r_D}=\frac{dI_D}{dU_F}=\frac{1}{U_T}(I_D+I_S)</math> | |||
Ponieważ w stanie przewodzenia <math>I_D >> I_S</math>. | |||
<math>\displaystyle g_D \approx \frac{I_D}{U_T}</math> | |||
potencjał elektrokinetyczny <math>U_T\,</math> w temperaturze 300 K jest równy około 26 mV | |||
<math>\displaystyle U_T=\frac{kT}{e}=\frac{1,38\cdot 10^{-23} J/K \cdot 300K}{1,6\cdot 10^{-19}C}=25,875mV</math> | |||
Zatem szukana wartość konduktancji <math>g_D\,</math> jest równa | |||
<math>\displaystyle g_D \approx \frac{I_D}{U_T}=\frac{3mA}{25,875mV}=0,0116S\approx 12mS</math> | |||
Pojemność dyfuzyjna diody Cd można obliczyć ze wzoru | |||
<math>\displaystyle C_d=t_t \frac{e}{kT}(I_D+I_S)\approx t_t \frac{eI_D}{kT}=t_t \frac{I_D}{U_T}=t_t\cdot g_0=5ns\cdot 12mS=0,6nF</math> | |||
'''Przykład 2''' | |||
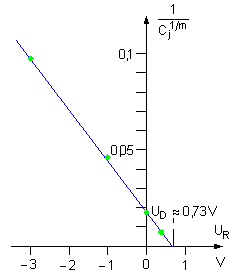
Wyznaczyć potencjał dyfuzyjny złącza i wykładnik m we wzorze Schottkyego jeżeli dla danych napięć <math>U_R\,</math> znamy pojemności diody C: | |||
0,4 V – 11 pF, 0 V – 7,4 pF, – 1 V – 4,9 V, – 3 V. – 3,4 pF. W obliczeniach uwzględnić pojemność obudowy diody <math>C_0 = 0,2 pF</math> | |||
'''Rozwiązanie:''' | |||
Metoda prób dobieramy wartość wykładnika m i rysujemy wykres funkcji <math>\displaystyle \left( \frac{1}{C_j(U_R)}\right)</math>, która powinna być linią prostą. Pojemność złącza obliczamy z zależności <math>C_j = C – C_0</math>. | |||
:[[Grafika:PEE_M13_Obraz1.gif]] | |||
|} | |} | ||
Wersja z 12:11, 16 sty 2007
 |
Modele elementów półprzewodnikowych |
 |
Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym . W stanie przewodzenia nadal obowiązuje wzór dla modelu dwuodcinkowego. |
 |
Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. Oznacza to, że rezystancja dynamiczna diody jest równa zeru. |
 |
Model idealnej diody. W tym wypadku dioda jest łącznikiem, który w stanie zaporowym jest wyłączony, a w stanie przewodzenia jest załączony. |
 |
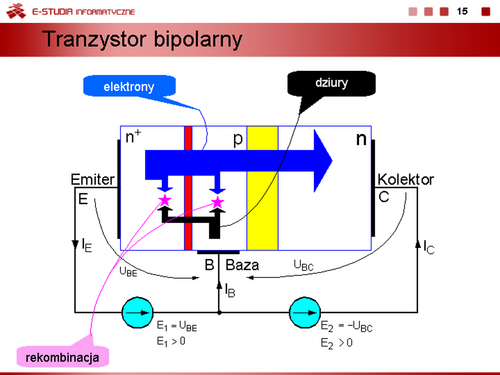
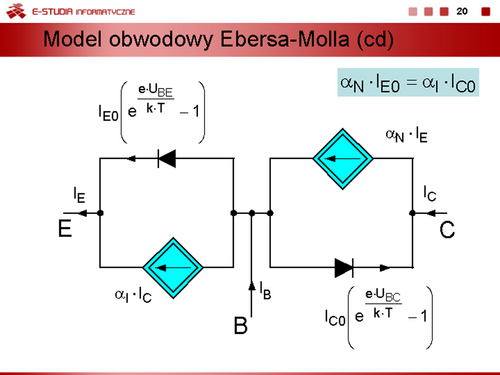
Można zatem zapisać równania, określające związki prądów , od napięć złączowych , w postaci
Równania te nazywamy równaniami Ebersa-Molla. |
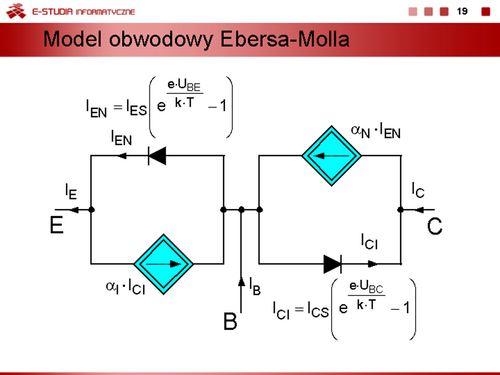 |
Bezpośrednią interpretacją obwodową równań ze slajdu 18 jest model przedstawiony na slajdzie 19. |