Programowanie funkcyjne/Strumienie

Czas rzeczywisty, a czas symulowany

Programowanie imperatywne i analogia obiektowa. Czas w modelowanym systemie jest modelowany przez czas w modelu systemu.

Programowanie strumieniowe --- nie ma takiej analogii z czasem. Staramy się w modelu oddać strukturę zależności, a niekoniecznie kolejność zdarzeń.

Strumień, to ciąg wartości --- cała, być może nieskończona, historia obiektu. Zamiast mówić o akcjach i zmianach stanu obiektów w danych chwilach patrzymy "jednym rzutem oka" na całą historię obiektu w czasoprzestrzeni. Staramy się oddać zależności między liniami świata jednych obiektów i innych.

Implementacja strumieni

Formalnie strumień to ciąg --- być może nieskończony. Pomysł polega jednak na tym, żeby był on "leniwy", tzn. obliczane były tylko potrzebne wartości. Tak więc strumień to para: wartość i odroczony strumień pozostałych wartości.

type 'a stream = Nil | Cons of 'a Lazy.t * 'a stream Lazy.t;;
  
let empty s = s = Nil;;
  
let head s = 
  match s with
    Nil -> failwith "Empty" |
    Cons (h, _) -> force h;;
  
let tail s = 
  match s with
    Nil -> failwith "Empty" |
    Cons (_, t) -> force t;; 
  
EXTEND ... Makro Cons
      

Cons zostaje zdefiniowane jako makro:

$\text{<mrow data-mjx-texclass="ORD">Cons</mrow>}(x,y)\equiv \text{<mrow data-mjx-texclass="ORD">Cons</mrow>}(\text{<mrow data-mjx-texclass="ORD">lazy</mrow>}x,\text{<mrow data-mjx-texclass="ORD">lazy</mrow>}y)$

Mając do dyspozycji takie konstruktory i selektory możemy zdefiniować kilka pomocniczych operacji na strumieniach:

let rec const_stream c = 
  Cons (c, const_stream c);; 
  
let ones = const_stream 1;;
  
let rec filter_stream p s = 
  if empty s then 
    Nil
  else 
    let h = head s 
    and t = tail s
    in 
      if p h then 
        Cons (h, filter_stream p t)
      else
        filter_stream p t;;
  
let rec stream_ref s n = 
  if n = 0 then 
    head s
  else
    stream_ref (tail s) (n - 1);;
  
let rec stream_map f s = 
  if empty s then 
    Nil
  else
    Cons (f (head s), stream_map f (tail s));;

Przykłady strumieni nieskończonych

Spróbujmy zdefiniować strumień liczb naturalnych:

let rec integers_from x = 
  Cons(x, integers_from (x+1));;
  
let nats = integers_from 0;;
      

Podobnie możemy zdefiniować strumień liczb Fibonacciego:

let fibs = 
  let rec fibo a b = 
    Cons (a, fibo b (a+b))
  in fibo 0 1;;
      

Jak widać, jeżeli jesteśmy w stanie skonstruować iteracyjną procedurę wyliczającą kolejne elementy strumienia, to tym samym jesteśmy w stanie zdefiniować strumień tych wartości. Procedura taka stanowi ukrytą w strumieniu "maszynerię", która na żądanie podaje kolejne elementy strumienia. Takie definicje strumieni nazywamy nie uwikłanymi(w odróżnieniu od uwikłanych, które poznamy dalej).W przypadku definicji nie uwikłanych bytem rekurencyjnym jest procedura, a nie strumień. Strumień jest wtórny wobec procedury rekurencyjnej.

Strumienie to tylko jeden ze sposobów konstruowania złożonych struktur danych, taki jak np. listy. Można więc tworzyć strumienie list, listy strumieni, czy strumienie strumieni. Oto przykład:

let rec tails s = 
  Cons (s, tails (tail s));;    
     

Strumień liczb pierwszych - sito Eratostenesa

Spróbujmy skonstruować nieskończony strumień liczb pierwszych, generowanych metodą sita Eratostenesa. Sposób konstrukcji takiego strumienia możemy przedstawić w postaci schematu przypominającego schematy blokowe układów przetwarzających sygnały. Strumienie są zaznaczone liniami ciągłymi, a pojedyncze wartości przerywanymi.

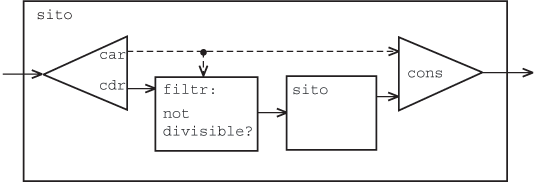
Schemat ten możemy zapisać w postaci następującego programu:

let sitko p s = 
  filter_stream (function x -> (x mod p) <> 0) s;;
  
let rec sito s  = 
  Cons (head s, sito (sitko (head s) (tail s)));;
  
let primes = 
  sito (integers_from 2);;

Definicje uwikłane

Definiując nieskończone strumienie nie musimy tego zawsze robić poprzez podanie odpowiedniej procedury rekurencyjnej (integers-from, fibgen, sieve).Możemy użyć elementów strumienia do zdefiniowania jego samego.

let rec ones =
  Cons (1, ones);;
      

Do budowy bardziej skomplikowanych strumieni potrzebujemy dodatkowych operacji budujących strumienie. Na przykład, do utworzenia strumienia liczb naturalnych czy liczb Fibonacciego potrzebujemy dodawania strumieni.

let rec add_int_streams s1 s2 = 
  if empty s1 or empty s2 then 
    Nil
  else
    Cons (head s1 + head s2, add_int_streams (tail s1) (tail s2));;
  
let rec nats =
  Cons (0, add_int_streams ones nats);;
      

Sposób obliczania kolejnych elementów strumieni zdefiniowanych w sposób uwikłany najlepiej przedstawić sobie w postaci tabelki:

$\begin{array}{cccccccccc}\text{<mrow data-mjx-texclass="ORD">ones</mrow>}& & 1& 1& 1& 1& 1& 1& 1& \dots \\ \text{<mrow data-mjx-texclass="ORD">nats</mrow>}& & 0& 1& 2& 3& 4& 5& 6& \dots \\ \text{<mrow data-mjx-texclass="ORD">nats</mrow>}& 0& 1& 2& 3& 4& 5& 6& 7& \dots \end{array}$

Zamiast dodawania strumienia jedynek, możemy użyć operacji zwiększania o jeden:

let succ x = x + 1;;
let rec nats = 
  Cons(0, stream_map succ nats);;
      

$\begin{array}{cccccccccc}\text{<mrow data-mjx-texclass="ORD">nats</mrow>}& & 0& 1& 2& 3& 4& 5& 6& \dots \\ \text{<mrow data-mjx-texclass="ORD">nats</mrow>}& 0& 1& 2& 3& 4& 5& 6& 7& \dots \end{array}$

let rec fibs = 
  Cons (0, Cons (1, add_int_streams fibs (tail fibs)));;
  
let tails s = 
  let rec w = 
    Cons (s, stream_map tail w)
  in w;;

Możemy też w uwikłany sposób zdefiniować strumień liczb pierwszych. Użyjemy do tego predykatu sprawdzającego, czy liczba jest pierwsza:

let rec primes = 
  Cons (2, filter_stream prime (integers_from 3))
      

Natomiast predykat prime zdefiniujemy używając ... strumienia liczb pierwszych:

and prime n = 
  let rec iter ps = 
    if square (head ps) > n then 
      true
    else if divisible n (head ps) then false
    else iter (tail ps)
  in 
    iter primes;;
     

Całość działa poprawnie, ponieważ strumień jest leniwą strukturą danych. Pierwszy element strumienia liczb pierwszych, 2, jest dany explicite. Natomiast sprawdzając kolejne liczby, czy są pierwsze, zawsze mamy już obliczone potrzebne liczby pierwsze.

Konkretnie, największa obliczona liczba pierwsza $p$ wystarcza do przetestowania pierwszości liczb do $p^2$ włącznie. Natomiast kolejna liczba pierwsza $p^{\prime }$ spełnia $p^{\prime }<2p\le p^2$.

$\begin{array}{ccccccccc}\text{<mrow data-mjx-texclass="ORD">integers<mi mathvariant="normal">\_</mi>from<mn>3</mn></mrow>}& & 3& 4,5& 6,7& 8,9,10,11& 12,13& 14,15,16,17& \dots \\ \text{<mrow data-mjx-texclass="ORD">filter<mi mathvariant="normal">\_</mi>stream</mrow>}\dots & & 3& 5& 7& 11& 13& 17& \dots \\ \text{<mrow data-mjx-texclass="ORD">primes</mrow>}& 2& 3& 5& 7& 11& 13& 17& \dots \\ \end{array}$

Iteracje jako strumienie

W przypadku definicji nie uwikłanych używaliśmy procedur iteracyjnych do zdefiniowania strumieni. Możemy ten mechanizm odwrócić i użyć strumieni do opisania procesów iteracyjnych - kolejne elementy strumienia mogą reprezentować kolejne kroki iteracji. Oto przykład, strumień kolejnych przybliżeń pierwiastka, metodą Newtona:

let sqrt_improve x g = (g +. x /. g) /. 2.0;;
  
let sqrt_stream x = 
  let rec guesses = 
    Cons (1.0, 
      stream_map (sqrt_improve x) guesses)
  in guesses;;
     

Spróbujmy przybliżyć liczbę $\pi$. Użyjemy do tego celu szeregu zbieżnego do $\frac{\pi }{4}$:

$\frac{\pi }{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$

let scale_stream c s = 
  stream_map (function x -> x *. c) s;;
  
let pi_summands = 
  let succ x = 
    if x > 0.0 then 
      -.x -. 2.0
    else
      -.x +. 2.0
  in
    let rec s = 
      Cons (1.0, stream_map succ s)
    in
      stream_map (fun x -> 1.0 /. x) s;;
  
let partial_sums s = 
  let rec ps = 
      Cons (head s, add_float_streams (tail s) ps)
  in ps;;
     
let pi_stream = scale_stream 4.0 (partial_sums (pi_summands 1.0));;
      

Taki strumień jest co prawda zbieżny, ale bardzo wolno. Po zsumowaniu pierwszych 1000 elementów ustalone są dopiero trzy pierwsze cyfry: $3.14$. Jest to dosyć oczywiste, jeżeli zauważymy, że suma pierwszych $n$ elementów jest obarczona błędem rzędu $\frac{1}{n}$

Można "przyspieszyć" zbieżność tego szeregu stosując "akcelerator Eulera". Jeśli $S_n$ jest sumą pierwszych $n$ wyrazów szeregu, to szereg zakcelerowany ma postać.

$S_{n+1}-\frac{(S_{n+1}-S_n{)}^2}{S_{n-1}-2S_n+S_{n+1}}$

Działa on dobrze dla ciągów o malejących modułach błędów przybliżenia.

Dlaczego on działa? Przedstawmy kolejne sumy częściowe szeregu w postaci granica plus błąd: $S_n=x+e_n$, $|e_n|>|e_n+1|>0$. Wówczas elementy przyspieszonego szeregu mają postać:

$\begin{array}{c}x+e_{n+1}-\frac{(x+e_{n+1}-x-e_n{)}^2}{x+e_{n-1}-2x-2e_n+x+e_{n+1}}=x+e_{n+1}-\frac{(e_{n+1}-e_n{)}^2}{e_{n-1}-2e_n+e_{n+1}}=\\ =x+\frac{e_{n+1}{e}_{n-1}-2e_{n+1}{e}_n+e_{n+1}^2-e_{n+1}^2+2e_n{e}_{n+1}-e_n^2}{e_{n-1}-2e_n+e_{n+1}}=x+\frac{e_{n+1}{e}_{n-1}-e_n^2}{e_{n-1}-2e_n+e_{n+1}}\end{array}$

Jeżeli np. $|e_n|=e\cdot c^n$ i znaki $e_n$ są takie same lub naprzemienne, to $e_{n+1}{e}_{n-1}-e_n^2=0$, czyli ciąg natychmiast osiąga granicę.

.... sprawdzić, kiedy można strumień wiele razy przyspieszać ...

Oto implementacja akceleratora Eulera:

let euler_transform st =
  let transform s = 
    let s0 = stream_ref s 0
    and s1 = stream_ref s 1
    and s2 = stream_ref s 2
    in (s2 -. square (s2 -. s1) /. (s0 -. 2.0 *. s1 +. s2))
  in
    stream_map transform (tails st);;
      

Taki strumień jest już zbieżny w rozsądnym czasie. Przeliczenie 1000 elementów przyspieszonego szeregu daje przybliżenie $3.141592653$. Jeszcze lepsze wyniki daje wielokrotne przyspieszanie. Skonstruujmy strumień kolejnych przyspieszeń strumienia sum częściowych i wybierzemy z niego strumień pierwszych elementów:

let rec pi_table = 
  Cons (pi_stream, stream_map euler_transform pi_table);;
  
let pi_stream_acc = stream_map head pi_table;;
  
let pi = stream_ref pi_stream_acc 8;;
      

Taki strumień już w 8 elemencie osiąga granice precyzji arytmetycznej.

Przykład: Trójkąt Pascala można sobie przedstawić jako strumień strumieni liczb całkowitych. Zdefiniuj w sposób uwikłany taki strumień.

$\begin{array}{ccccccc}1& 1& 1& 1& 1& 1& \dots \\ 1& 2& 3& 4& 5& 6& \dots \\ 1& 3& 6& 10& 15& 21& \dots \\ 1& 4& 10& 20& 35& 56& \dots \\ 1& 5& 15& 35& 70& 126& \dots \\ 1& 6& 21& 56& 126& 252& \dots \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \end{array}$

Strumienie par - liczby Ramanujana

Przedstawimy teraz jako przykład operowania strumieniami, konstrukcję strumienia liczb Ramanujana. Liczby Ramanujana to takie liczby naturalne, które można przedstawić jako sumy sześcianów dwóch liczb naturalnych na dwa różne sposoby. Pierwsze z tych liczb, to: 1729, 4104, 13832, 20683. Niech waga pary liczb naturalnych to będzie suma sześcianów jej składowych. Pomysł konstrukcji strumienia liczb Ramanujana polega na skonstruowaniu strumienia (nieuporządkowanych) par liczb naturalnych uporządkowanego wg. niemalejących wag, wychwyceniu par o powtarzających się wagach i wypisaniu tych wag.

Następująca procedura łączy dwa strumienie uporządkowane wg. niemalejących wag elementów w jeden uporządkowany strumień. Waga jest określona w postaci funkcji w

let rec merge_weighted w s1 s2 = 
  if empty s1 then s2 else
  if empty s2 then s1 else 
    let h1 = head s1 
    and h2 = head s2
    in 
      if w h1 < w h2 then 
        Cons (h1, merge_weighted w (tail s1) s2)
      else if w h1 > w h2 then 
        Cons (h2, merge_weighted w s1 (tail s2))
      else if h1 = h2 then 
        Cons (h1, merge_weighted w (tail s1) (tail s2))
      else 
        Cons (h1, Cons (h2, merge_weighted w (tail s1) (tail s2)));;
      

Następujące definicje określają wagi par oraz funkcję tworzącą strumień par uporządkowanych wg. wag.

let cube x = x * x * x;;
  
let weight (x, y) = cube x + cube y;;
   
let rec pairs s = 
  Cons ((head s, head s), 
        merge_weighted 
          weight
          (stream_map (function x -> (head s, x)) (tail s))
          (pairs (tail s)));;
      

Następująca procedura pozostawia jedynie reprezentantów sekwencji elementów o powtarzających się wagach.

let rec non_uniq w s = 
  let rec skip we s =
    if empty s then Nil 
    else if we = w (head s) then skip we (tail s)
    else s
  in
    'if empty s then Nil 
    else if empty (tail s) then Nil 
    else
      let h1 = head s
      and h2 = head (tail s)
      in 
        if w h1 = w h2 then 
          Cons (w h1, non_uniq w (skip (w h1) s))
        'else
          non_uniq w (tail s);;
     

Strumień liczb Ramanujana możemy zdefiniować następująco:

let ramanujan = 
  in non_uniq weight (pairs nats);;

Co jeszcze ...

Strumienie jako reprezentacja danych, np. szeregów potęgowych. Operacje na funkcjach reprezentowanych w taki sposób.

Laboratoria i ćwiczenia

Laboratoria i ćwiczenia do wykładu