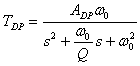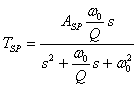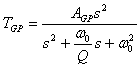PEE Lab 3: Różnice pomiędzy wersjami

Wersja z 06:54, 25 paź 2006

Ćwiczenie Nr 3: Badanie filtrów bikwadratowych i charakterystyk częstotliwościowych układów

Ćwiczenie jest ćwiczeniem wirtualnym. Student wykonuje pełny program badań przez Internet, wykorzystując opracowane do tego celu programy interakcyjne umieszczone poniżej

Badanie filtru bikwadratowego KHN

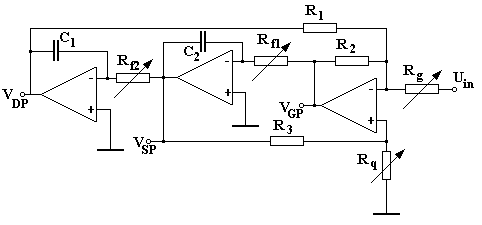
Schemat filtru KHN (Kerwina-Heulsmana-Newcomba [1]) wykorzystującego 3 wzmacniacze operacyjne przedstawiony jest na rys. 1.

Rys. 1 Schemat filtru bikwadratowego KHN

Filtr ten realizuje trzy podstawowe typy filtrów o następujących transmitancjach

i charakterystyce fazowej opisanej wzorem:

i charakterystyce fazowej opisanej wzorem:

i charakterystyce fazowej opisanej wzorem:

Projektować będziemy filtr o zadanej wartości częstotliwości środkowej $f_{0}$ , dobroci $Q$ oraz wartości wzmocnienia w paśmie $A$ . Dla zadanych wartości tych parametrów należy obliczyć wartości rezystancji rezystorów i pojemności kondensatorów korzystając z następujących wzorów:

Przy założeniu: $C_{1} = C_{2} = C$ , $R_{1} = R_{2} = R_{3} = R_{4} = R$ oraz $R_{f 1} = R_{f 2} = R_{f}$ Przyjmuje się: $R = 20 k W$ oraz $C = 1 n F$ lub $C = 11 n F$ . Wartości elementów oblicza się wg wzorów:

lub lub

Na rys. 2 przedstawiono ikonę programu umożliwiającego zadawanie dowolnej wartości parametrów.

Rys. 2 Ikona programu do badania filtru KHN

Program badań:

Zaprojektować filtr KHN o podanych parametrach:

Filtr dolnoprzepustowy

ADP = 2, f0=500Hz, Q = 1, dla C1 = C2 = 11nF ADP = 1, f0=1500Hz, , dla C1 = C2 = 11nF ADP = 0,1, f0=100Hz, , dla C1 = C2 = 11nF Filtr środkowoprzepustowy

ASP = 2, f0=200Hz, Q = 2, dla C1 = C2 = 11nF ASP = 4, f0=550Hz, , dla C1 = C2 = 11nF ASP = 0,5, f0=1000Hz, Q = 5, dla C1 = C2 = 11nF

Filtr górnoprzepustowy

AGP = 3, f0=5000Hz, Q = 1, dla C1 = C2 = 1nF AGP = 1, f0=1500Hz, , dla C1 = C2 = 1nF AGP = 0,1, f0=10000Hz, , dla C1 = C2 = 1nF

Zbadać jak wpływa zmiana o niewielkie wartości (do 10%) rezystorów Rf1, Rf2 i RQ na parametry filtru. Skorzystać z poniższej tabeli oznaczając strzałkami zmiany wielkości: ä (wzrost), æ (zmniejszenie), b.z. (bez zmian). Badanie przeprowadzić dla 3 wybranych filtrów o różnych parametrach.

PEE Lab 3: Różnice pomiędzy wersjami

Wersja z 06:54, 25 paź 2006

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia

@@ Linia 24: / Linia 24: @@
 Przyjmuje się: <math>R = 20 kW</math> oraz <math>C = 1 nF</math> lub <math>C = 11 nF</math>.
 Wartości elementów oblicza się wg wzorów:
+[[Grafika:PEE_Lab_3_Rf.gif]]
+[[Grafika:PEE_Lab_3_RG1_DP.gif]] lub [[Grafika:PEE_Lab_3_RG1_SP.gif]] lub [[Grafika:PEE_Lab_3_RG1_GP.gif]]
+[[Grafika:PEE_Lab_3_RQ.gif]]
+Na rys. 2 przedstawiono ikonę programu umożliwiającego zadawanie dowolnej wartości parametrów.
+Rys. 2 Ikona programu do badania filtru KHN
+Program badań:
+Zaprojektować filtr KHN o podanych parametrach:
+Filtr dolnoprzepustowy
+ADP = 2, f0=500Hz, Q = 1, dla C1 = C2 = 11nF
+ADP = 1, f0=1500Hz, , dla C1 = C2 = 11nF
+ADP = 0,1, f0=100Hz, , dla C1 = C2 = 11nF
+Filtr środkowoprzepustowy
+ASP = 2, f0=200Hz, Q = 2, dla C1 = C2 = 11nF
+ASP = 4, f0=550Hz, , dla C1 = C2 = 11nF
+ASP = 0,5, f0=1000Hz, Q = 5, dla C1 = C2 = 11nF
+Filtr górnoprzepustowy
+AGP = 3, f0=5000Hz, Q = 1, dla C1 = C2 = 1nF
+AGP = 1, f0=1500Hz, , dla C1 = C2 = 1nF
+AGP = 0,1, f0=10000Hz, , dla C1 = C2 = 1nF
+Zbadać jak wpływa zmiana o niewielkie wartości (do 10%) rezystorów Rf1, Rf2 i RQ na parametry filtru. Skorzystać z poniższej tabeli oznaczając strzałkami zmiany wielkości: ä (wzrost), æ (zmniejszenie), b.z. (bez zmian). Badanie przeprowadzić dla 3 wybranych filtrów o różnych parametrach.