Układy elektroniczne i technika pomiarowa/Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd2.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd2.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|W niniejszym wykładzie będą zaprezentowane podstawowe rodzaje filtrów stosowanych w układach elektronicznych. Omówione zostaną właściwości prostych filtry pasywne typu RC, RL i RLC oraz niektórych rodzajów filtrów aktywnych, które w swojej strukturze zawierają wzmacniacze operacyjne. | ||
Podstawowym zadaniem filtrów jest wytłumienie, z punktu widzenia zastosowania danego układu elektronicznego, niepożądanych częstotliwości występujących w sygnale sterującym. | |||
Układy filtrów dzieli się, przyjmując odpowiednie kryteria, na różne grupy. Jednym | |||
z najistotniejszych jest podział ze względu na pasmo częstotliwości, które jest tłumione przez filtr. Wyróżniamy tu filtry: | |||
*dolnoprzepustowe, | |||
*górnoprzepustowe, | |||
*pasmowoprzepustowe, w tym szerokopasmowe i wąskopasmowe (selektywne) | |||
*pasmowo zaporowe, które tłumią sygnały w określonym paśmie częstotliwości. | |||
Inne kryteria jakie bierze się pod uwagę w klasyfikacji filtrów to np. kształt charakterystyk częstotliwościowych: amplitudowej i fazowej, rodzaj zastosowanych elementów, technologia wykonania. | |||
Ważną cechą filtru jest jego rząd. Stosuje się filtry I, II i wyższych rzędów. Im wyższy rząd filtru tym bardziej strome zbocza na krańcach pasma przenoszenia i tym bardziej idealna (prostokątna) charakterystyka częstotliwościowa (amplitudowa). | |||
Ważnym kryterium podziału filtrów wynika z rodzaju sygnałów jakie są przetwarzane. Wyróżnia my tu filtry analogowe, które są przedmiotem niniejszego wykładu | |||
i filtry cyfrowe. | |||
|} | |} | ||
---- | ---- | ||
| Linia 13: | Linia 27: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd3.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd3.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Układy pasywne''' | ||
Filtry pasywne to układy, które w swojej strukturze zawierają elementy pasywne: rezystory, kondensatory i dławiki indukcyjne. Zaleta takich układów jest to, że mogą przenosić duże moce, a zatem mogą być stosowane w urządzeniach energoelektronicznych (np. w układach prostowników, falowników itp.). ponadto mają prostą konstrukcję i nie wymagają dodatkowych źródeł zasilania. | |||
W technice sygnałowej dla wielkich częstotliwości wymiary geometryczne oraz indukcyjności dławików są bardzo małe i dlatego często w tej sytuacji wykorzystuje się do konstrukcji filtru istniejące w układzie rzeczywistym indukcyjności montażowe | |||
|} | |} | ||
---- | ---- | ||
| Linia 19: | Linia 37: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd4.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd4.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Filtr dolnoprzepustowy''' | ||
Dwie wersje filtru RC i RL przedstawiono na slajdzie. Właściwości obu układów w dziedzinie częstotliwości i czasu są identyczne. | |||
Opis w dziedzinie częstotliwości | |||
Załóżmy, że w filtrze RC iloczyn RC, a w filtrze RL iloraz L/R jest równy <math>\tau = T</math>. | |||
Stałą τ nazywamy stałą czasową obwodu RC lub RL. | |||
Transmitancję widmową filtru można opisać zależnością: | |||
<math>\frac{u_2(j\omega)}{u_1(j\omega)}=T(j\omega)\frac{1}{1+j\omega T}</math> | |||
Moduł transmitancji widmowej i faza sygnału wyjściowego względem wejściowego po znormalizowaniu pulsacji przebiegu względem pulsacji granicznej <math>\omega_g</math> jest równy: | |||
<math>|T(jx)|=\frac{1}{\sqrt{1+x^2\omega^2_gT^2}}=\frac{1}{\sqrt{1+x^2}}</math> | |||
<math>\varphi=arctg(x\omega_gT)=arctg</math> | |||
gdzie: | |||
<math>x=\frac{\omega}{\omega_g} (0<x<\infty)</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 25: | Linia 62: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd5.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd5.png|thumb|500px]] | ||
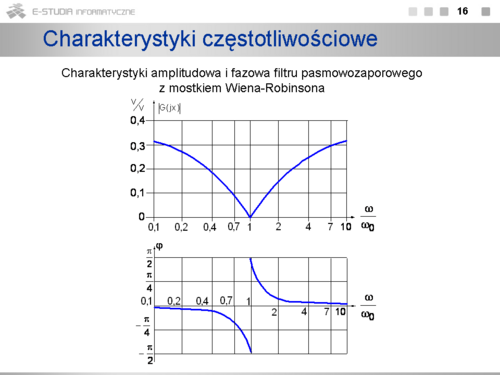
|valign="top"| | |valign="top"|Charakterystyki częstotliwościowe modułu (amplitudową) i przesunięcia fazowego (fazową) przedstawiono na rysunku. Pulsacja graniczna <math>\omega_g</math> lub częstotliwość graniczna fg filtru to taka wartość <math>\omega</math> lub f, przy której moduł zmniejsza się w stosunku do tego jaki jest przy niskich częstotliwościach o 3dB, tzn. jest równy <math>\frac{1}{\sqrt{2}}</math> . | ||
Z zależności 5.2 wynika, że | |||
<math>\omega_g=\frac{1}{T}</math> | |||
lub | |||
<math>f_g=\frac{1}{2\pi T}</math> | |||
Przesunięcie fazowe dla tej częstotliwości jest równe <math>\varpi=-\frac{\pi}{4}</math> | |||
Charakterystyka amplitudowa opada z prędkością 20 dB / dekadę. | |||
Jeżeli wymagana jest większa prędkość opadania charakterystyki można połączyć kaskadowo n filtrów dolnoprzepustowych. Wypadkowa transmitancja widmowa będzie w tym wypadku równa iloczynowi transmitancji poszczególnych filtrów, | |||
a liczba n będzie mówiła o rzędzie filtru. | |||
|} | |} | ||
---- | ---- | ||
| Linia 31: | Linia 82: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:UETP_M5_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:UETP_M5_Slajd6.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Opis w dziedzinie czasu''' | ||
Opis w dziedzinie czasu polega na badaniu odpowiedzi układu na wymuszenie standardowe. Najczęściej stosuje się wymuszenie w postaci skoku jednostkowego. Na slajdzie przedstawiono odpowiedź układów RC i RL przy załączeniu i wyłączeniu napięcia wejściowego. | |||
W przypadku złączenia napięcie wyjściowe zmienia się wykładniczo zgodnie | |||
z zależnością: | |||
<math>u_2(t)=U_M\Bigg(1-e^{-\frac{t}{\tau}}\Bigg)</math> | |||
|} | |} | ||
---- | ---- | ||
Wersja z 12:59, 20 paź 2006
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |