SW wykład 10 - Slajd6

<<powrót do strony wykładu

Poprawność programów i weryfikacja Poprawność programów Dowodzenie poprawności Wyspecyfikowany program Logika Hoare'a Definicje formalne Definicje formalne, c.d. Semantyka logiki Hoare'a Reguły wnioskowania Przykład dowodu Przykład dowodu, c.d. Niezmiennik pętli Przykład dowodu, c.d. W pełni wyspecyfikowany program Teorie pierwszego rzędu

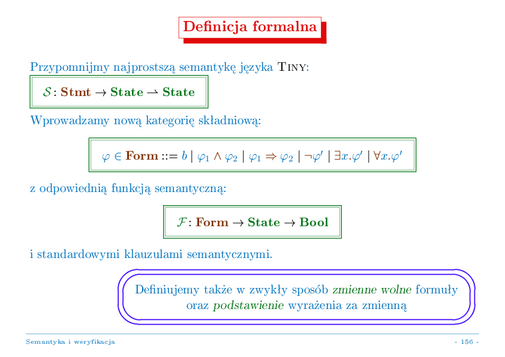
Wprowadzone wyżej, nieformalne rozumienie stwierdzeń o częściowej poprawności instrukcji względem warunków wstępnego i końcowego, zastąpimy teraz ścisłą definicją, sformułowaną w terminach semantyki języka TINY i wykorzystywanych formuł pierwszego rzędu.

Przypomnijmy z wykładu 4 (slajdy 5, 6, 9, 10), gdzie podsumowaliśmy składnię języka (w szczególności jego instrukcji) i podaliśmy zdefiniowaliśmy jego formalną semantykę, że znaczeniami instrukcji języka TINY są funkcje częściowe ze stanów w stany, gdzie stany są po prostu funkcjami ze zbioru zmiennych z wartości liczbowe.

Wprowadźmy teraz nową kategorię syntaktyczną, służącą budowaniu specyfikacji instrukcji w jeżyku TINY, mianowicie formuły pierwszego rzędu. Formuły te budowane są z wyrażeń logicznych języka TINY, przez łączenie ich zwykłymi spójnikami logicznymi i kwantyfikację. Zwykłe (znane choćby z zajęć "Logika i teoria mnogości") pojęcia wolnego i związanego wystąpienia zmiennej w formule oraz podstawienia termu (wyrażenia arytmetycznego) w formule za zmienną (z uniknięciem przechwytywania zmiennych wolnych przez kwantyfikatory) stosują się tu w oczywisty sposób.

Znaczeniami takich formuł są funkcje ze stanów w wartości logiczne.

Pomijamy tu formalną definicję funkcji semantycznej przez podanie klauzul semantycznych dla wszystkich konstrukcji budujących formuły (a więc dla formuł będących wyrażeniami logicznymi, gdy po prostu zastosować należy semantykę dla takich wyrażeń, oraz dla formuł budowanych przez spójniki logiczne i kwantyfikatory, gdzie zapisać po prostu trzeba standardowe definicje spełniania takich formuł, znane z zajęć "Logika i teoria mnogości").