MO Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 119: | Linia 119: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M10_Slajd21.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M10_Slajd21.png|thumb|500px]] | ||
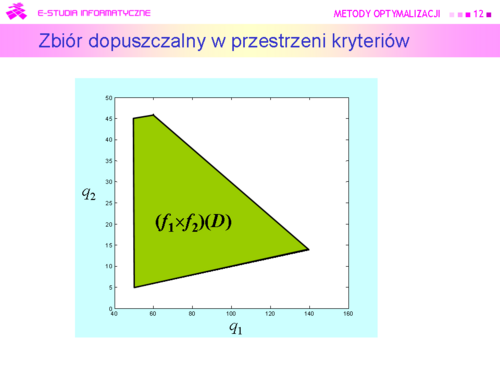
|valign="top"| | |valign="top"|Ponieważ zbiór Pareto w przestrzeni kryteriów w zadaniu decyzyjnym pana X jest następujący | ||
, | |||
to podejście utylitarianistyczne oparte na maksymalizacji sumy | |||
jako rozwiązanie da oraz decyzję – tylko pracować. (Dobrze jest wykonać stosowny rysunek.) | |||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M10_Slajd22.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M10_Slajd22.png|thumb|500px]] | ||
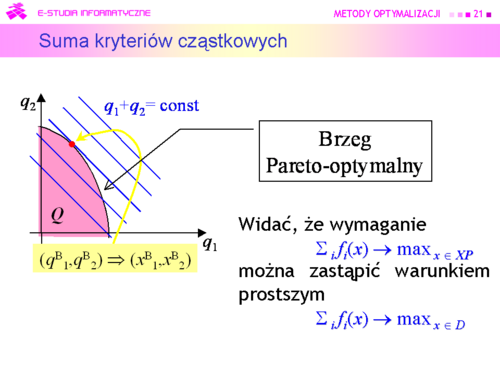
|valign="top"| | |valign="top"|Przypisanie wag poszczególnym kryteriom oznacza posłużenie się funkcją | ||
, | |||
gdzie współczynnik b można interpretować jako cenę jednostki zadowolenia. | |||
Zauważmy, że dla b = 5/2, każdy punkt ze zbioru Pareto daje tą samą wartość funkcji ub, dla b < 5/2 rozwiązaniem będzie i –punkt „wymuszony” przez ograniczenia: dostępnego czasu i nieujemności wariantów. Dla b > 5/2 jako rozwiązanie otrzymamy oraz – punkt „wymuszony” przez ograniczenia: dostępnego czasu oraz przyjętej maksymalnej liczby godzin przeznaczonych na czytanie. (Dobrze jest wykonać stosowne rysunki.) | |||
|} | |} | ||
---- | ---- | ||
| Linia 137: | Linia 146: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M10_Slajd24.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M10_Slajd24.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Podejście oparte na zasadzie sprawiedliwości jako rozwiązanie da | ||
oraz jako wybrany wariant . | |||
Nie zawsze prosta o nachyleniu 45° przecina zbiór Pareto ! | |||
|} | |} | ||
---- | ---- | ||
| Linia 155: | Linia 167: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M10_Slajd27.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M10_Slajd27.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Punkt idealny dla pana X to , punkt nadiru . Dla metryki euklidesowej najbliższym punktu idealnego w zbiorze Pareto jest punkt czyli wybranymi wariantami powinna być para . | ||
Dla tej samej metryki, punktem najdalej położonym w stosunku do nadiru jest punkt określony przez warianty (tylko pracować). | |||
(Dobrze jest wykonać stosowne rysunki.) | |||
|} | |} | ||
---- | ---- | ||
Wersja z 16:22, 9 paź 2006
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
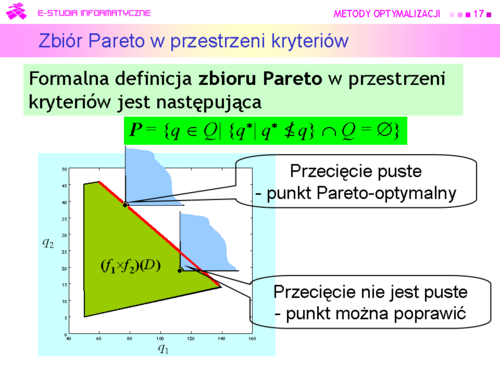 |
 |
 |
 |
 |
 |
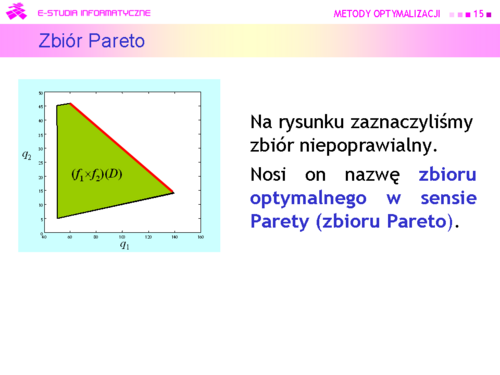
Podejście oparte na zasadzie sprawiedliwości jako rozwiązanie da
oraz jako wybrany wariant . Nie zawsze prosta o nachyleniu 45° przecina zbiór Pareto ! |
 |
 |
 |
 |