|
|
| Linia 124: |
Linia 124: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:MO_M1_Slajd19.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd19.png|thumb|500px]] |
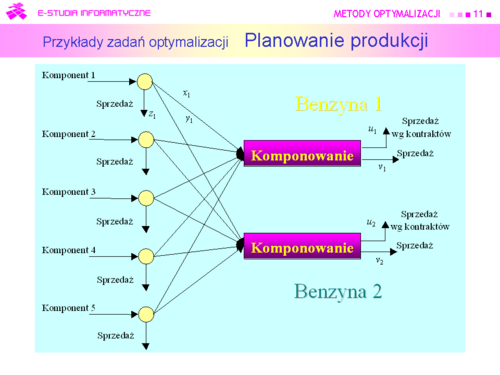
| |valign="top"|Współczynniki<math> \eta_i</math> i <math>\mu_j</math> można traktować dla benzyn np. jako liczbę oktanową. | | |valign="top"|Współczynniki <math> \eta_i</math> i <math>\mu_j</math> można traktować dla benzyn np. jako liczbę oktanową. |
| |} | | |} |
| ---- | | ---- |
| Linia 202: |
Linia 202: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:MO_M1_Slajd32.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd32.png|thumb|500px]] |
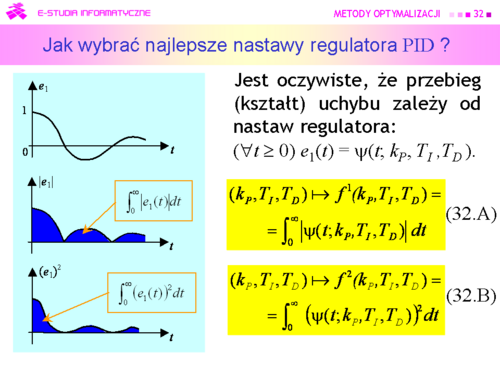
| |valign="top"|Zatem do oceny “odległości od zera” uchybu możemy posłużyć się całką z modułu uchybu (32.A), albo całką z kwadratu uchybu (32.B). | | |valign="top"|Zatem do oceny "odległości od zera” uchybu możemy posłużyć się całką z modułu uchybu (32.A), albo całką z kwadratu uchybu (32.B). |
| |} | | |} |
| ---- | | ---- |
| Linia 299: |
Linia 299: |
| |width="500px" valign="top"|[[Grafika:MO_M1_Slajd48.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M1_Slajd48.png|thumb|500px]] |
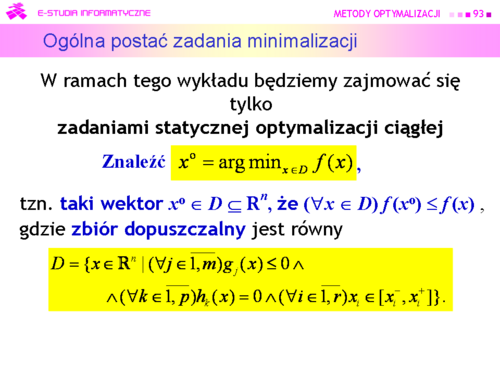
| |valign="top"|Przypadku | | |valign="top"|Przypadku |
| <math>x_i^- = -\infty albo x_i^+ = \infty</math>, | | <math>x_i^- = -\infty</math> albo <math>x_i^+ = \infty</math>, |
| nie wykluczamy | | nie wykluczamy |
|
| |
|