SW wykład 8 - Slajd2

<<powrót do strony wykładu

Częściowe porządki zupełne Przykłady Funkcje ciągłe Intuicje Intuicje, c.d. Przestrzeń funkcji częściowych Twierdzenie o punkcie stałym Techniki dowodowe Semantyka while

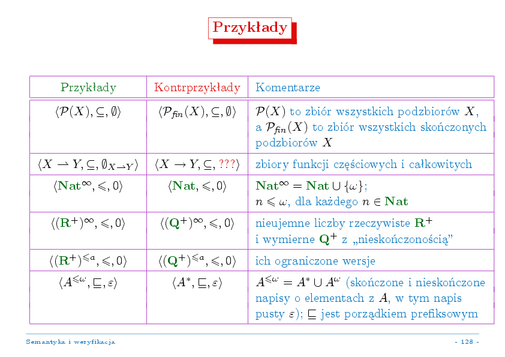
Kilka przykładów:

Rodzina wszystkich podzbiorów danego zbioru, uporządkowana przez inkluzję, jest zbiorem łańcuchowo zupełnym ze zbiorem pustym jako elementem najmniejszym. Kresy górne są po prostu sumami rodzin podzbiorów danego zbioru. Warto zatem dodać, że istnieją tu kresy górne wszystkich elementów --- taki zbiór uporządkowany, w którym istnieją kresy górne wszystkich jego podzbiorów nazywamy kratą zupełną. Warto może sobie tu przypomnieć definicję kresu dolnego i pokazać, że w kratach zupełnych każdy podzbiór ma też kres dolny.

Uwaga: jeśli ograniczymy się tylko do skończonych podzbiorów danego zbioru, to na ogół nie będą one stanowiły zbioru łańcuchowo zupełnego: łatwo podać przykład łańcucha skończonych podzbiorów danego (nieskończonego) zbioru, który nie ma skończonego ograniczenia górnego, a więc nie ma też kresu górnego w rodzinie skończonych podzbiorów danego zbioru.

Rodzina wszystkich funkcji częściowych między dwoma zbiorami, uporządkowana prze inkluzję (grafów funkcji częściowych, czyli funkcji częściowych rozumianych jako zbiory par) jest zbiorem łańcuchowo zupełnym, z funkcją pustą (nigdzie nie określoną) jako elementem najmniejszym. Dwie funkcje są tu w relacji porządku, gdy jedna z nich jest zawarta w drugiej, to znaczy: gdy ta pierwsza jest określona, to ta druga też jest określona i daje ten sam wynik, ale dodatkowo ta druga może też być określona na argumentach, dla których ta pierwsza określona nie jest. Łatwo teraz sprawdzić, że mając łańcuch (czy nawet zbiór skierowany) funkcji częściowych, suma teoriomnogościowa tych funkcji też jest funkcją częściową i jest ona kresem górnym tego łańcucha (czy zbioru skierowanego) funkcji.

Częściowość funkcji jest tu kluczowa: funkcje całkowite z taką relacją porządku na ogół nie tworzą zbioru łańcuchowo zupełnego. Choć bowiem łańcuchy są tu tylko trywialne (jednoelementowe), więc zawsze mają kres górny, to na ogół nie istnieje tu element najmniejszy (poza trywialnym przypadkiem, gdy zbiór, w który prowadzą funkcje, jest jednoelementowy).

Liczby naturalne, ze zwykłym porządkiem i z dodanym elementem "nieskończonym" (większym od wszystkich liczb naturalnych) tworzą zbiór łańcuchowo zupełny z zerem jako elementem najmniejszym. Kres górny każdego skończonego łańcucha to jego największy element, a kres górny każdego łańcucha nieskończonego to dodany element "nieskończony".

Zauważmy, że w zbiorze liczb naturalnych bez dodanego elementu "nieskończonego" łańcuchy nieskończone nie mają ograniczeń górnych --- nie jest on zatem zbiorem łańcuchowo zupełnym.

Trochę podobnie, nieujemne liczby rzeczywiste, ze zwykłym porządkiem i dodanym elementem "nieskończonym" tworzą zbiór łańcuchowo zupełny z zerem jako elementem najmniejszym. Ale już nieujemne liczby wymierne, ze zwykłym porządkiem i dodanym elementem "nieskończonym" nie tworzą zbioru łańcuchowo zupełnego --- istnieją w nich przeliczalne łańcuchy, których kres górny w tym zbiorze nie istnieje (rosnące ciągi liczb wymiernych zbieżne do liczby niewymiernej).

Zupełnie podobnie, nieujemne liczby rzeczywiste niewiększe niż ustalona liczba rzeczywista, ze zwykłym porządkiem tworzą zbiór łańcuchowo zupełny, a dopowiedni zbiór liczb wymiernych zbioru łańcuchowo zupełnego nie tworzy.

I jeszcze jeden ważny przykład: rozpatrzmy skończone słowa nad ustalonym alfabetem, uporządkowane przez relacje "bycia prefiksem". Łatwo sprawdzić, że relacja ta jest (częściowym) porządkiem i że najmniejszym elementem w tym zbiorze jest słowo puste. Łatwo też pokazać, że łańcuchy słów o nieograniczonej długości nie mają w tym zbiorze ograniczeń górnych, a wiec i nie mają kresu górnego. Na przykład ciąg coraz dłuższych słów powtarzających tę samą literę jest tu łańcuchem bez ograniczenia górnego (a więc i bez kresu górnego). Nie jest to zatem zbiór łańcuchowo zupełny. Dodajmy jednak do niego (przeliczalne, o pozycjach numerowanych liczbami naturalnymi) słowa nieskończone, rozszerzając relacje "bycia prefiksem" w oczywisty sposób. Teraz z kolei łatwo sprawdzić, że każdy łańcuch ma tu kres górny. Łańcuchy słów o ograniczonej długości są skończone, a kresem górnym takiego łańcucha jest zawarte w nim najdłuższe słowo --- łatwo sprawdzić, że w łańcuchu nie może być tu dwóch różnych słów o tej samej długości. Z kolei każdy łańcuch słów skończonych o nieograniczonej długości to zbiór prefiksów pewnego słowa nieskończonego, które jest kresem górnym tego łańcucha. W końcu, każdy łańcuch może zawierać co najwyżej jedno słowo nieskończone i jeśli takie słowo zawiera, to jest ono w nim elementem największym i jego kresem górnym.

Podobne przykłady można mnożyć. Co więcej, podamy wkrótce konstrukcje, które pozwalają na budowanie coraz bardziej złożonych zbiorów łańcuchowo zupełnych z prostszych składowych.