Logika dla informatyków/Logika intuicjonistyczna

Logika intuicjonistyczna

Logika klasyczna oparta jest na pojęciu wartości logicznej zdania. Poprawnie zbudowane i jednoznaczne stwierdzenie jest w tej logice klasyfikowane jako "prawdziwe" lub "fałszywe". Wartość logiczna zdania złożonego (np. implikacji) jest zaś ustalana na podstawie wartości jego składowych (niezależnie od ich faktycznej treści). W większości przypadków takie postępowanie jest naturalne i wygodne. Ale nie zawsze. Przypomnijmy na przykład, że klasyczna materialna implikacja nie zawsze odpowiada jakiejkolwiek faktycznej zależności pomiędzy przesłanką i konkluzją (Rozdział 3.1). Inną konsekwencją dwuwartościowości logiki klasycznej jest prawo wyłączonego środka. Akceptujemy alternatywę $p\vee \mathrm{\neg }p$, niezależnie od tego czy zdanie $p$ jest faktycznie prawdziwe czy fałszywe, a nawet nie wiedząc, co dokładnie to zdanie wyraża. Zilustrujmy to na przykładzie:

Fakt 11.1

Istnieją takie liczby niewymierne $x$ i $y$, że $x^y$ jest liczbą wymierną.

Dowód

Jeśli ${\sqrt{2}}^{\sqrt{2}}$ jest wymierne, to można przyjąć $x=y=\sqrt{2}$, w przeciwnym przypadku niech $x={\sqrt{2}}^{\sqrt{2}}$ i $y=\sqrt{2}$.

Powyższy dowód, przy całej swojej prostocie i elegancji, ma pewną oczywistą wadę: nadal nie wiemy, jakie liczby naprawdę spełniają żądany warunek. A oto inny dowód Faktu $(11.1)$.

Dowód 2

Dla $x=\sqrt{2}$ oraz $y=2{\log }_{2}3$ mamy $x^y=3$.

Mówimy, że drugi dowód, w odróżnieniu od pierwszego, jest konstruktywny. Oczywiście, konstruktywny dowód zawiera w sobie więcej przydatnej informacji niż niekonstruktywny, ale z punktu widzenia logiki klasycznej, oba te dowody są tak samo poprawne.

Logika, dopuszczająca tylko wnioskowania o charakterze konstruktywnym, znana jest pod tradycyjną, nieco mylącą, nazwą logiki intuicjonistycznej. W tej logice nie przypisujemy zdaniom wartości logicznych. Nieformalne objaśnienie zasad logiki intuicjonistycznej posługuje się pojęciem konstrukcji. Zdanie jest uważane za prawdziwe, gdy można podać jego konstrukcję, tworzoną według następujących zasad (od nazwisk Brouwera, Heytinga i Kołmogorowa zwanych interpretacją BHK):

• Konstrukcja dla $\phi \wedge \psi$ polega na podaniu konstrukcji dla $\phi$ i konstrukcji dla $\psi$;
• Konstrukcja dla $\phi \vee \psi$ polega na wskazaniu jednego ze składników $\phi$, $\psi$ i podaniu konstrukcji dla tego składnika.
• Konstrukcja dla implikacji $\phi \to \psi$ to metoda (funkcja) przekształcająca każdą konstrukcję przesłanki $\phi$ w konstrukcję dla konkluzji $\psi$.
• Nie ma konstrukcji dla fałszu $\mathrm{\perp }$.
• Konstrukcja dla $\mathrm{\forall }x\phi (x)$ to metoda, która każdej potencjalnej wartości $a$ zmiennej $x$ przypisuje konstrukcję dla $\phi (a)$.
• Konstrukcja dla $\mathrm{\exists }x\phi (x)$ polega na wskazaniu pewnej wartości $a$ zmiennej $x$, oraz konstrukcji dla $\phi (a)$.

Negacja intuicjonistyczna $\mathrm{\neg }\phi$ utożsamiana jest z implikacją $\phi \to \mathrm{\perp }$. A zatem

• Konstrukcja dla $\mathrm{\neg }\phi$ to metoda obracająca każdą ewentualną konstrukcję $\phi$ w absurd ("rzecz, której nie ma").

Nie od rzeczy jest tu nastepująca uwaga: o konstrukcji dla $\phi \to \psi$ można myśleć jak o funkcji typu $\phi \to \psi$, bo przecież konstrukcjom dla $\phi$ (obiektom "typu $\phi$") przypisuje ona konstrukcje dla $\psi$, czyli obiekty "typu $\psi$". Za chwilę wrócimy do tej analogii.

Przykład 11.2

Konstrukcję dla formuły $p\to \mathrm{\neg }\mathrm{\neg }p$ możemy zapisać tak:

Przypuśćmy, że dana jest konstrukcja $C$ dla przesłanki $p$. Wtedy konstrukcja dla konkluzji $\mathrm{\neg }\mathrm{\neg }p$ (czyli dla $(p\to \mathrm{\perp })\to \mathrm{\perp }$) jest następująca: daną konstrukcję dla formuły $p\to \mathrm{\perp }$ należy zastosować do $C$.

Próba podania konstrukcji dla implikacji odwrotnej $\mathrm{\neg }\mathrm{\neg }p\to p$ natrafia jednak na nieprzezwyciężalną trudność. Aby wykorzystać daną konstrukcję dla $(p\to \mathrm{\perp })\to \mathrm{\perp }$, musielibyśmy mieć konstrukcję dla $p\to \mathrm{\perp }$, a skoro jej nie mamy, to założenie jest bezużyteczne.

Niemożliwe jest też wskazanie konstrukcji dla schematu $p\vee \mathrm{\neg }p$, nie znając $p$ nie możemy bowiem wskazać żadnego z członów alternatywy.

Podobnie będzie na przykład z implikacją $\mathrm{\forall }x(q\vee p(x))\to q\vee \mathrm{\forall }xp(x)$. Konstrukcja przesłanki dla każdej wartości $a$ zmiennej $x$ generuje albo konstrukcję dla $q$ albo konstrukcję dla $p(a)$. Ale skorzystać z niej można tylko dla konkretnych wartości $a$. Tymczasem, aby podać konstrukcję dla konkluzji, musielibyśmy umieć podjąć krytyczną decyzję "w ciemno".

Proponujemy teraz Czytelnikowi wykonanie Ćwiczenia 2, a nastepnie próbę znalezienia konstrukcji dla formuł z Ćwiczenia 5.

Intuicjonistyczny rachunek zdań

Objaśnienia odwołujące się do pojęcia konstrukcji są tylko nieformalne. Ścisłą definicję logiki intuicjonistycznej może stanowić system wnioskowania, na przykład w stylu naturalnej dedukcji. Dla uproszczenia ograniczymy się tutaj do intuicjonistycznego rachunku zdań. System naturalnej dedukcji dla takiego rachunku, przedstawiony poniżej można uważać za uściślenie interpretacji BHK. Otrzymujemy go z systemu klasycznego (Sekcja 5.2) przez odrzucenie reguły PS.<ref name="czternascie">Robimy to, zauważając z pewną satysfakcją, że właśnie ta reguła "nie pasuje" do pozostałych, bo odbiega swoją formą od zasady wprowadzania i eliminacji spójników.</ref>

$(\to$ -intro Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle ) \hspace{.2cm} \frac{\Delta,\varphi\vdash\psi}{\Delta\vdash\varphi\to\psi} \hspace{1cm} (\to } -elim Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle ) \hspace{.2cm} \frac{\Delta\vdash\varphi\to\psi\qquad \Delta\vdash\varphi}{\Delta\vdash\psi}}

$(\wedge$ -intro Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle )\hspace{.2cm} \frac{\Delta\vdash\varphi\qquad \Delta\vdash\psi}{\Delta\vdash\varphi\wedge\psi} \hspace{1cm} (\wedge } -elim Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle ) \hspace{.2cm}\frac{\Delta\vdash\varphi\wedge\psi}{\Delta\vdash\varphi} \hspace{1cm} (\wedge } -elim Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle ) \hspace{.2cm}\frac{\Delta\vdash\varphi\wedge\psi}{\Delta\vdash\psi}}

$(\vee$ -intro Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle )\hspace{.2cm} \frac{\Delta\vdash\varphi}{\Delta\vdash\varphi\vee\psi} \hspace{1cm} (\vee } -intro Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle )\hspace{.2cm} \frac{\Delta\vdash\psi}{\Delta\vdash\varphi\vee\psi} }

$(\vee$ -elim Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle )\hspace{.2cm} \frac{\Delta\vdash\varphi\vee\psi\qquad \Delta,\varphi\vdash\vartheta\qquad \Delta,\psi\vdash\vartheta}{\Delta\vdash\vartheta}}

Ciekawy jest sposób w jaki z klasycznego rachunku sekwentów (Sekcja 5.3) można otrzymać system dla logiki intuicjonistycznej. Otóż należy w tym celu ograniczyć liczbę formuł występujących po prawej stronie sekwentów do (co najwyżej) jednej, przy czym sekwent $\mathrm{\Gamma }⊢$ z pustą prawą stroną można utożsamiać z sekwentem $\mathrm{\Gamma }⊢\mathrm{\perp }$. Reguła $(\vee$ -prawa $)$ traci wtedy sens i trzeba ją zastąpić przez dwie reguły podobne do tych z Ćwiczenia 11 w Rozdziale 5. Pozostałe reguły pozostają w zasadzie bez zmian.

$(\to$ -lewa Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle )\hspace{.2cm} \frac{\Delta\vdash\varphi\hspace{1cm} \Delta,\psi\vdash\vartheta}{\Delta,\varphi\to\psi\vdash\vartheta} \hspace{1cm}(\to } -prawa Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle )\hspace{.2cm} \frac{\Delta,\varphi\vdash\psi}{\Delta\vdash\varphi\to\psi}}

$(\wedge$ -lewa Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle )\hspace{.2cm} \frac{\Delta,\varphi,\psi\vdash\vartheta}{\Delta,\varphi\wedge\psi\vdash\vartheta} \hspace{1cm} (\wedge } -prawa Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle )\hspace{.2cm} \frac{\Delta\vdash \varphi\hspace{1cm} \Delta\vdash\psi}{\Delta\vdash\varphi\wedge\psi}}

$(\vee$ -lewa Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle )\hspace{.2cm} \frac{\Delta, \varphi\vdash\vartheta\hspace{1cm} \Delta,\psi\vdash\vartheta}{\Delta, \varphi\vee\psi \vdash\vartheta} \hspace{1cm} \frac{\Delta\vdash \varphi}{\Delta\vdash \varphi\vee\psi}\hspace{.2cm}(\vee } -prawa Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle )\hspace{.2cm} \frac{\Delta\vdash \psi}{\Delta\vdash \varphi\vee\psi}}

Intuicjonistyczny system dowodzenia w stylu Hilberta dla logiki zdaniowej, w której występuje tylko implikacja i fałsz, a negacja $\mathrm{\neg }\phi$ jest zdefiniowana jako $\phi \to \mathrm{\perp }$, otrzymamy bardzo łatwo: wystarczy usunąć aksjomat $\mathrm{\neg }\mathrm{\neg }\phi \to \phi$ z systemu klasycznego i dodać jeden nowy:

$(A3i)\mathrm{\perp }\to \phi$.

Ale aksjomaty (B1)-(B4) z Rozdziału 5 do logiki intuicjonistycznej nie pasują, bo nie zgadzają się z interpretacją BHK. Trzeba więc przyjąć aksjomaty z Ćwiczenia 2 do Rozdziału 6, które zamiast definiować koniunkcję i alternatywę, wyrażają ich najważniejsze własności.

$(D1)\phi \to \phi \vee \psi$;

$(D2)\psi \to \phi \vee \psi$;

$(D3)(\phi \to \vartheta )\wedge (\psi \to \vartheta )\to (\phi \vee \psi \to \vartheta )$;

$(C1)\phi \wedge \psi \to \phi$;

$(C2)\phi \wedge \psi \to \psi$;

$(C3)(\vartheta \to \phi )\wedge (\vartheta \to \psi )\to (\vartheta \to \phi \wedge \psi )$.

Fakt 11.3

Opisane powyżej intuicjonistyczne systemy dowodzenia (naturalna dedukcja, rachunek sekwentów oraz system Hilberta) są sobie równoważne: formuła $\phi$ jest twierdzeniem dowolnego z tych systemów , gdy jest twierdzeniem każdego z pozostałych.

Dowód

Ćwiczenie.

Semantyka topologiczna

Jak już powiedzieliśmy, logika intuicjonistyczna różni się od klasycznej tym, że nie odwołuje się do pojęcia wartości logicznej, a formalna definicja jest syntaktyczna (przez system dowodzenia) a nie semantyczna. Okazuje się jednak, że intuicjonistyczny rachunek zdań ma ciekawą semantykę topologiczną. Stanowi ona uogólnienie semantyki klasycznego rachunku zdań z  Ćwiczenia 7 do Rozdziału 1. Różnica polega na tym, że znaczeniami formuł mogą być jedynie zbiory otwarte.

Definicja 11.4

Niech ${𝒪}$ będzie rodziną wszystkich podzbiorów otwartych zbioru liczb rzeczywistych $\mathbb{ℝ}$. Dla $A\subseteq \mathbb{ℝ}$, przez $\mathrm{I}\mathrm{n}\mathrm{t}(A)$ oznaczymy wnętrze zbioru $A$, tj. największy zbiór otwarty zawarty w $A$. Wartościowaniem w zbiorze ${𝒪}$ nazwiemy dowolną funkcję $\varrho :ZZ\to {𝒪}$. Dla danego $\varrho$, możemy każdej formule zdaniowej przypisać wartość w ${𝒪}$:

• ${\Vert \mathrm{\perp }\Vert }_{\varrho }=\mathrm{\varnothing }$ oraz ${\Vert \mathrm{\top }\Vert }_{\varrho }=\mathbb{ℝ}$;
• ${\Vert p\Vert }_{\varrho }=\varrho (p)$, gdy $p$ jest symbolem zdaniowym;
• ${\Vert \mathrm{\neg }\phi \Vert }_{\varrho }=\mathrm{I}\mathrm{n}\mathrm{t}(\mathbb{ℝ}-{\Vert \phi \Vert }_{\varrho })$;
• Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle \left\Vert\varphi\vee\psi\right\Vert_\varrho=\left\Vert\varphi\right\Vert_\varrho}\cup \left\Vert\psi\right\Vert_\varrho} ;
• Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle \left\Vert\varphi\wedge\psi\right\Vert_\varrho=\left\Vert\varphi\right\Vert_\varrho}\cap \left\Vert\psi\right\Vert_\varrho}} ;
• $\Vert \phi \to \psi \Vert \varrho =\mathrm{I}\mathrm{n}\mathrm{t}((\mathbb{ℝ}-{\Vert \phi \Vert }_{\varrho })\cup {\Vert \psi \Vert }_{\varrho })$.

Powiemy, że formuła $\phi$ jest prawdziwa w $\mathbb{ℝ}$, gdy jej wartością jest cały zbiór $\mathbb{ℝ}$.

Twierdzenie 11.5

Formuła rachunku zdań jest intuicjonistycznym twierdzeniem wtedy i tylko wtedy, gdy jest prawdziwa w $\mathbb{ℝ}$.

Uwaga: Implikacja "tylko wtedy" w Twierdzeniu 11.5 zachodzi nie tylko dla liczb rzeczywistych, ale także dla dowolnej przestrzeni topologicznej.

Przykład 11.6

Aby się przekonać, że prawo wyłączonego środka nie jest twierdzeniem logiki intuicjonistycznej, przypuśćmy, że $\varrho (p)=(0,\mathrm{\infty })$. Wtedy $\Vert p\vee \mathrm{\neg }p{\Vert }_{\varrho }=\mathbb{ℝ}-\{0\}\ne \mathbb{ℝ}$.

Jeśli zaś $\varrho (p)=\mathbb{ℝ}-\{1\}$ to także $\Vert \mathrm{\neg }\mathrm{\neg }p\to p{\Vert }_{\varrho }=\mathbb{ℝ}-\{1\}$, więc i formuła $\mathrm{\neg }\mathrm{\neg }p\to p$ nie jest intuicjonistycznym twierdzeniem.

Normalizacja dowodów

Wróćmy teraz do systemu naturalnej dedukcji dla intuicjonistycznego rachunku zdań. Dla uproszczenia ograniczmy się na razie do tzw. minimimalnej logiki implikacyjnej, tj. do formuł zbudowanych z pomocą samej implikacji. Przypuśćmy, że mamy taki dowód:

W tym dowodzie najpierw wprowadzamy implikację, a zaraz potem ją eliminujemy. Można jednak zrobić inaczej. Tam gdzie w części (2) dowodu używane jest założenie $\phi$ można po prostu wstawić całą część (1). Chociaż rozmiary nowego dowodu mogą być większe (założenie $\phi$ mogło być używane kilkakrotnie) to jednak jego struktura będzie prostsza. Docelowo możemy uzyskać dowód, w którym takie sytuacje jak na rysunku w ogóle nie występują. Taki dowód nazwiemy dowodem normalnym. Proces normalizacji dowodu jest podobny do procesu eliminacji cięcia, a dowody normalne mają podobne zalety jak dowody bez cięcia. W szczególności, wyszukiwanie dowodu dla danej formuły staje się łatwiejsze, jeśli można się ograniczyć do dowodów normalnych.

Lambda-termy z typami

Normalizacja dowodów ma bliski związek z rachunkiem lambda. Przypomnijmy tu podstawowe definicje.

Definicja 11.7

Przyjmijmy, że mamy pewien przeliczalny nieskonczony zbior zmiennych przedmiotowych. Termy rachunku lambda (lambda-termy) określamy przez indukcję:

• Zmienne przedmiotowe są termami.
• Jesli $M$ i $N$ są termami, to math>\displaystyle (MN)</math> tez.
• Jesli $M$ jest termem i $x$ jest zmienną, to $(\lambda xM)$ jest termem.

Wyrażenie postaci $(MN)$ nazywamy aplikacją, a wyrażenie postaci $(\lambda xM)$ to $\lambda$-abstrakcja. Stosujemy nastepujące konwencje notacyjne:

- opuszczamy zewnętrzne nawiasy;

- aplikacja wiąże w lewo, tj. $MNP$ oznacza $(MN)P$;

- piszemy $\lambda x_1\dots x_n.M$ zamiast $\lambda x_1(\dots (\lambda x_{n}M)\cdots )$.

Uwaga: kropka w wyrażeniu $\lambda x_1\dots x_n.M$ zastępuje lewy nawias, którego zasięg rozciąga się do końca wyrażenia $M$. Zwyczajowo używa się też notacji $\lambda x.M$.

Operator lambda-abstrakcji $\lambda$, podobnie jak kwantyfikator, wiąże zmienne, tj. wszystkie wystąpienia $x$ w wyrażeniu $\lambda xM$ uwaza się za związane. Zazwyczaj lambda-termy rozważa się z dokładnością do alfa-konwersji, tj. utożsamia się termy różniące się tylko zmiennymi związanymi.

Pominiemy tu ścisłą definicję podstawienia $M[N/x]$, która jest podobna do definicji stosowanej dla formuł z kwantyfikatorami.

Definicja 11.8

Relacja beta-redukcji to najmniejsza relacja w zbiorze lambda-termow, spełniająca warunki:

- $(\lambda xP)Q{\to }_{\beta }P[Q/x]$;

- jesli $M{\to }_{\beta }{M}^{\prime }$, to $MN{\to }_{\beta }{M}^{\prime }N$, $NM{\to }_{\beta }N{M}^{\prime }$ oraz $\lambda xM{\to }_{\beta }\lambda x{M}^{\prime }$.

Inaczej mówiąc, $M{\to }_{\beta }{M}^{\prime }$ zachodzi gdy podterm termu $M$ postaci $(\lambda xP)Q$, czyli redeks, zostaje zamieniony na wynik podstawienia $P[Q/x]$. Znakiem ${\hookrightarrow }_{\beta }$ oznaczamy domknięcie przechodnio-zwrotne relacji ${\to }_{\beta }$. Mówimy, że term jest w postaci normalnej, gdy nie zawiera żadnego redeksu, tj. nie redukuje się.

Zauważmy tu analogię pomiędzy redukcją $(\lambda xP)Q{\to }_{\beta }P[Q/x]$ i wywołaniem procedury $P$, przy którym na miejsce parametru formalnego $x$ podstawiony zostaje parametr aktualny $Q$.

Definicja 11.9

Przyjmijmy pewien zbiór typów atomowych, który oznaczymy przez $ZZ$ (zbieżność oznaczeń jest nieprzypadkowa). Powiemy teraz, że

• Typy atomowe są typami;
• Jeśli $\sigma$ i $\tau$ są typami, to $\sigma \to \tau$ jest typem.

A zatem nasze typy to po prostu formuły zdaniowe zbudowane przy pomocy samej implikacji. Stosujemy taką konwencję, że strzałka jest łączna w prawo, tj. napis $\sigma \to \tau \to \rho$ oznacza $\sigma \to (\tau \to \rho )$.

Przez otoczenie typowe rozumiemy zbiór deklaracji postaci $(x:\tau )$, gdzie $x$ jest zmienną (przedmiotową) a $\tau$ jest typem. Żądamy przy tym, aby otoczenie było funkcją, tj. aby jedna zmienna nie była deklarowana dwa razy. Przez $\mathrm{\Gamma }(x:\sigma )$ oznaczamy otoczenie określone tak:

$\mathrm{\Gamma }(x:\sigma )(y)=\{\begin{array}{ll}\mathrm{\Gamma }(y),& \text{jeśli }y\ne x;\\ \sigma ,& \text{w przeciwnym przypadku.}\end{array}$

Lambda-termom można teraz przypisywać typy. Napis $M:\tau$ stwierdza, że $M$ jest termem typu $\tau$. Interpratecja operatora $\to$ jest taka: Term typu $\tau \to \sigma$ zaaplikowany do argumentu typu $\tau$ daje wynik typu $\sigma$. Ponieważ typ termu może zależeć od typów jego zmiennych wolnych, więc nasz system przypisania typów wyprowadza asercje postaci $\mathrm{\Gamma }⊢M:\tau$, gdzie $\mathrm{\Gamma }$ jest otoczeniem typowym.

Aksjomat: $\mathrm{\Gamma }(x:\sigma )⊢x:\sigma$

Reguły:

$\frac{\mathrm{\Gamma }(x:\sigma )⊢M:\tau }{\mathrm{\Gamma }⊢(\lambda xM):\sigma \to \tau }(Abs)\frac{\mathrm{\Gamma }⊢M:\sigma \to \tau \mathrm{\Gamma }⊢N:\sigma }{(MN):\tau }(App)$

Ważne, że takie przypisanie typu zachowuje się przy beta-redukcji.

Fakt 11.10

Jeśli $\mathrm{\Gamma }⊢M:\tau$ oraz $M{\to }_{\beta }N$, to $\mathrm{\Gamma }⊢N:\tau$.

Izomorfizm Curry'ego-Howarda (formuły-typy)

Uderzające podobieństwo pomiędzy regułami przypisania typów i regułami dowodzenia w naturalnej dedukcji bywa nazywane izomorfizmem Curry'ego-Howarda. Lambda-termy z typami prostymi, to w istocie to samo co dowody w logice minimalnej. Bez wchodzenia w szczegóły sformułujmy tu najważniejszą konsekwencję tego izomorfizmu.

Fakt 11.11

Formuła implikacyjna $\phi$ jest twierdzeniem intuicjonistycznym , gdy istnieje zamknięty (tj. bez zmiennych wolnych) lambda-term typu $\phi$.

Związek pomiędzy dowodami i lambda-termami staje się jeszcze bardziej interesujący, gdy zauważymy podobieństwo dowodu ze strony 84 do beta-redeksu postaci $(\lambda xP)Q$:

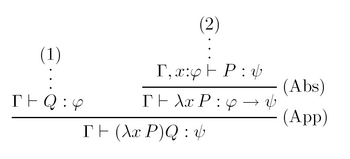
Normalizacja tamtego dowodu daje w wyniku dowód, którego odpowiednikiem jest term $P[Q/x]$. Ewaluacja lambda-termów (beta-redukcja) ściśle więc reprezentuje zjawisko normalizacji dowodów. W szczególności okazuje się, że dowodom normalnym odpowiadają termy w postaci normalnej. Ma to niebagatelne znaczenie w związku z następującym twierdzeniem, którego (nietrywialny) dowód pomijamy.

Twierdzenie 11.12

Każdy term z typami prostymi można zredukować do postaci normalnej.

Wniosek z Twierdzeń 11.10-11.12 jest taki: aby ustalić czy formuła $\phi$ ma dowód, należy zbadać, czy istnieje zamknięty term typu $\phi$ w postaci normalnej. W ten sposób można np. rozstrzygnąć, które z formuł w Ćwiczeniu 6 są twierdzeniami intuicjonistycznymi.

Technika wyszukiwania dowodu danej formuły za pomocą konstrukcji odpowiedniego lambda-termu daje się uogólnić dla języków znacznie bogatszych niż zdaniowa logika implikacyjna i znajduje zastosowanie w systemach wspomagających dowodzenie, takich jak system Coq.

Przykład 11.13

W myśl interpretacji BHK, konstrukcją (dowodem) koniunkcji $\phi \wedge \psi$ jest para konstrukcji, jedna "typu $\phi$" a druga "typu $\psi$". W naturalnej dedukcji, reguła wprowadzania koniunkcji odpowiada tworzeniu takiej pary, a reguła eliminacji koniunkcji reprezentuje rzutowanie na jedną ze współrzędnych. A więc koniunkcja tak naprawdę to samo co produkt kartezjański. Jeśli rozszerzymy rachunek lambda o pary (rekordy) i rzutowania, będziemy mogli napisać takie reguły przypisania typów zawierających znak koniunkcji.

$\frac{\mathrm{\Gamma }⊢M:\phi \mathrm{\Gamma }⊢N:\psi }{\mathrm{\Gamma }⊢⟨M,N⟩:\phi \wedge \psi }\frac{\mathrm{\Gamma }⊢M:\phi \wedge \psi }{\mathrm{\Gamma }⊢{\pi }_1(M):\phi }\frac{\mathrm{\Gamma }⊢M:\phi \wedge \psi }{\mathrm{\Gamma }⊢{\pi }_2(M):\psi }$

Przypisy

<references/>