MN04LAB: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
mNie podano opisu zmian |
||
| Linia 132: | Linia 132: | ||
bardziej nawet małe zaburzenia <math>\displaystyle f</math> mogą spowodować duże przemieszczenie jej | bardziej nawet małe zaburzenia <math>\displaystyle f</math> mogą spowodować duże przemieszczenie jej | ||
miejsca zerowego. | miejsca zerowego. | ||
Zauważ, iż dla wielokrotnych miejsc zerowych, <math>\displaystyle \mbox{cond} _{abs} (f^{-1},0) = \infty</math>. Zgadza się to z intuicją, bo może się zdarzyć, że nawet minimalne zaburzenie <math>\displaystyle f</math> | Zauważ, iż dla wielokrotnych miejsc zerowych, <math>\displaystyle \mbox{cond} _{abs} (f^{-1},0) = \infty</math>. Zgadza się to z intuicją, bo może się zdarzyć, że nawet minimalne zaburzenie <math>\displaystyle f</math> | ||
spowoduje, iż miejsc zerowych po prostu nie będzie... | spowoduje, iż miejsc zerowych po prostu nie będzie... | ||
</div></div></div> | |||
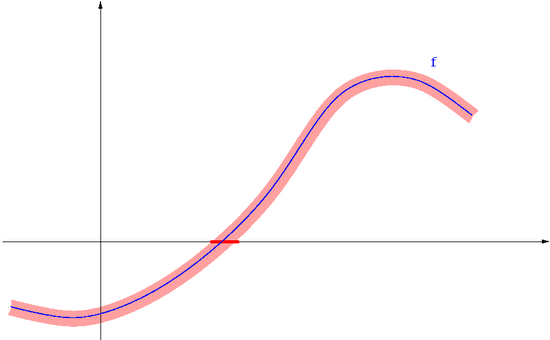
[[Image:MNnonlinearcond2.png|thumb|550px|center|Gdy trochę zaburzymy wartości funkcji <math>\displaystyle f</math>, dobrze uwarunkowane miejsce zerowe nie przemieści się zbyt daleko od miejsca zerowego <math>\displaystyle f</math>.]] | |||
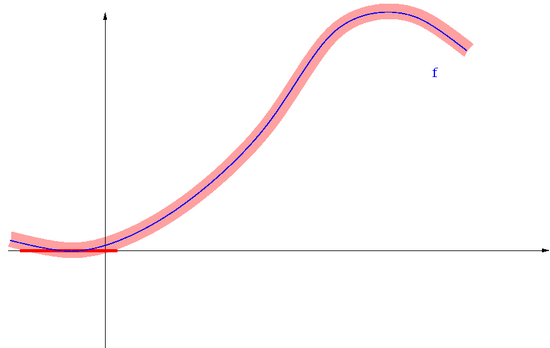
[[Image:MNnonlinearcond4.png|thumb|550px|center|Gdy trochę zaburzymy wartości funkcji <math>\displaystyle f</math>, źle uwarunkowane miejsce zerowe może przemieścić się bardzo daleko od miejsca zerowego <math>\displaystyle f</math>.]] | [[Image:MNnonlinearcond4.png|thumb|550px|center|Gdy trochę zaburzymy wartości funkcji <math>\displaystyle f</math>, źle uwarunkowane miejsce zerowe może przemieścić się bardzo daleko od miejsca zerowego <math>\displaystyle f</math>.]] | ||
Wersja z 21:09, 29 wrz 2006
Uwarunkowanie zadania i algorytmy numerycznie poprawne.
<<< Powrót do strony głównej przedmiotu Metody numeryczne
Oglądaj wskazówki i rozwiązania __SHOWALL__
Ukryj wskazówki i rozwiązania __HIDEALL__
Ćwiczenie
Aby obliczyć można zastosować dwa algorytmy: oraz . Pokazać, że oba algorytmy są numerycznie poprawne, ale drugi z nich wywołuje mniejszy błąd względny wyniku w przypadku, gdy i .
Rozwiązanie
Ćwiczenie
Pokazać, że naturalny algorytm obliczania cosinusa kąta między dwoma wektorami Parser nie mógł rozpoznać (nieznana funkcja „\inR”): {\displaystyle \displaystyle a, b\inR^n} ,
jest numerycznie poprawny. Oszacować błąd względny wyniku w .
Ćwiczenie
Podaj przykład funkcji , której miejsce zerowe ma wspólczynnik uwarunkowania
- mały
- duży
Rozwiązanie