MN04LAB: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
<!-- | |||
Konwertowane z pliku LaTeX przez latex2mediawiki, zob. http://www.ii.uj.edu.pl/ pawlik1/latex2mediawiki.php. | |||
Niezb�dne rozszerzenia i modyfikacje oryginalnego latex2mediawiki | |||
wprowadzi� przykry@mimuw.edu.pl | |||
--> | |||
=Uwarunkowanie zadania i algorytmy numerycznie poprawne.= | |||
{{powrot |Metody numeryczne | do strony głównej | |||
przedmiotu <strong>Metody numeryczne</strong>}} | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"> | |||
Oglądaj wskazówki i rozwiązania __SHOWALL__<br> | |||
Ukryj wskazówki i rozwiązania __HIDEALL__ | |||
</div> | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie</span> | <span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie</span> | ||
| Linia 9: | Linia 26: | ||
<math>\displaystyle rd_\nu(a)=a</math> i <math>\displaystyle rd_\nu(b)=b</math>. | <math>\displaystyle rd_\nu(a)=a</math> i <math>\displaystyle rd_\nu(b)=b</math>. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | |||
Rzeczywiście, dla pierwszego algorytmu obliczony w <math>\displaystyle fl_\nu</math> wynik <math>\displaystyle \tilde{s}</math> spełnia | |||
<center><math>\displaystyle | |||
\tilde{s} = fl_\nu(fl_\nu(a\cdot a)-fl_\nu(b\cdot b)) = (a^2(1+\epsilon_a) - b^2(1+\epsilon_b))(1+\epsilon_{-}), | |||
</math></center> | |||
gdzie <math>\displaystyle |\epsilon_{a}|, |\epsilon_{b}|, |\epsilon_{-}| \leq \nu</math>. A więc jesteśmy w sytuacji, gdy --- jeśli tylko <math>\displaystyle |a|\approx |b|</math> --- może nastąpić redukcja cyfr przy odejmowaniu... | |||
Natomiast drugi algorytm w ogóle nie jest na to czuły, | |||
<center><math>\displaystyle | |||
\tilde{s} = fl_\nu(fl_\nu(a - b) \times fl_\nu(a + b)) = ((a-b)(1+\epsilon_{-}) \cdot (a+b)(1+\epsilon_{+}))(1+\epsilon_{\times}), | |||
</math></center> | |||
gdzie znów <math>\displaystyle |\epsilon_{+}|, |\epsilon_{-}|, |\epsilon_{\times}| \leq \nu</math>. | |||
Ponieważ ostatecznie | |||
<center><math>\displaystyle | |||
\tilde{s} = (a-b)(a+b)(1+\epsilon_{-})(1+\epsilon_{+})(1+\epsilon_{\times})= | |||
= (a^2 - b^2)(1+E), | |||
</math></center> | |||
gdzie <math>\displaystyle |E| \leq 3\nu</math>, algorytm drugi będzie <strong>zawsze</strong> dawał wynik obarczony małym błędem względnym. | |||
Zwróć uwagę na istotną rolę przyjętego założenia, że <math>\displaystyle a</math> i <math>\displaystyle b</math> są liczbami maszynowymi, reprezentowanymi dokładnie w <math>\displaystyle fl_\nu</math>. W praktyce obliczeniowej, najczęściej właśnie z takimi danymi będziemy się spotykać... | |||
</div></div></div> | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
| Linia 25: | Linia 68: | ||
w <math>\displaystyle fl_\nu</math>. | w <math>\displaystyle fl_\nu</math>. | ||
</div></div> | </div></div> | ||
<!-- | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
| Linia 65: | Linia 110: | ||
</div></div> | </div></div> | ||
--> | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie</span> | <span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie</span> | ||
| Linia 86: | Linia 133: | ||
miejsca zerowego. | miejsca zerowego. | ||
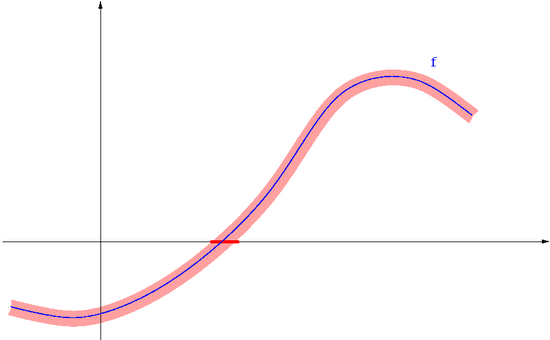
Zauważ, | [[Image:MNnonlinearcond2.png|thumb|550px|center|Gdy trochę zaburzymy wartości funkcji <math>\displaystyle f</math>, dobrze uwarunkowane miejsce zerowe nie przemieści się zbyt daleko od miejsca zerowego <math>\displaystyle f</math>.]] | ||
Zgadza się to z intuicją, bo może się zdarzyć, że nawet minimalne zaburzenie <math>\displaystyle f</math> | |||
spowoduje, | Zauważ, iż dla wielokrotnych miejsc zerowych, <math>\displaystyle \mbox{cond} _{abs} (f^{-1},0) = \infty</math>. Zgadza się to z intuicją, bo może się zdarzyć, że nawet minimalne zaburzenie <math>\displaystyle f</math> | ||
spowoduje, iż miejsc zerowych po prostu nie będzie... | |||
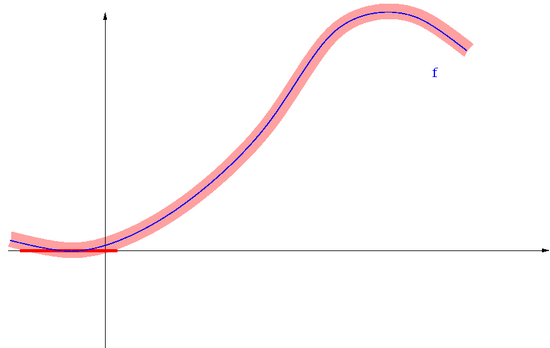
[[Image:MNnonlinearcond4.png|thumb|550px|center|Gdy trochę zaburzymy wartości funkcji <math>\displaystyle f</math>, źle uwarunkowane miejsce zerowe może przemieścić się bardzo daleko od miejsca zerowego <math>\displaystyle f</math>.]] | |||
</div></div></div> | </div></div></div> | ||
Wersja z 21:04, 29 wrz 2006
Uwarunkowanie zadania i algorytmy numerycznie poprawne.
<<< Powrót do strony głównej przedmiotu Metody numeryczne
Oglądaj wskazówki i rozwiązania __SHOWALL__
Ukryj wskazówki i rozwiązania __HIDEALL__
Ćwiczenie
Aby obliczyć można zastosować dwa algorytmy: oraz . Pokazać, że oba algorytmy są numerycznie poprawne, ale drugi z nich wywołuje mniejszy błąd względny wyniku w przypadku, gdy i .
Rozwiązanie
Ćwiczenie
Pokazać, że naturalny algorytm obliczania cosinusa kąta między dwoma wektorami Parser nie mógł rozpoznać (nieznana funkcja „\inR”): {\displaystyle \displaystyle a, b\inR^n} ,
jest numerycznie poprawny. Oszacować błąd względny wyniku w .
Ćwiczenie
Podaj przykład funkcji , której miejsce zerowe ma wspólczynnik uwarunkowania
- mały
- duży
Rozwiązanie