Układy elektroniczne i technika pomiarowa/Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
| Linia 184: | Linia 184: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:UETP_M10_Slajd23.png]] | |valign="top" width="500px"|[[Grafika:UETP_M10_Slajd23.png]] | ||
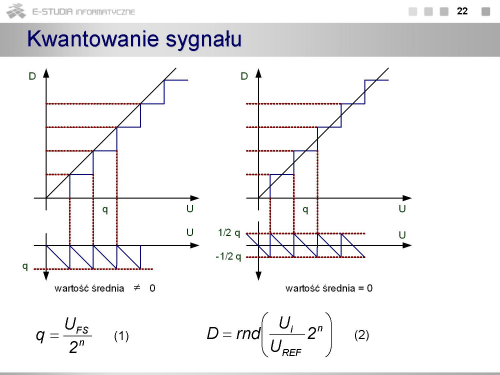
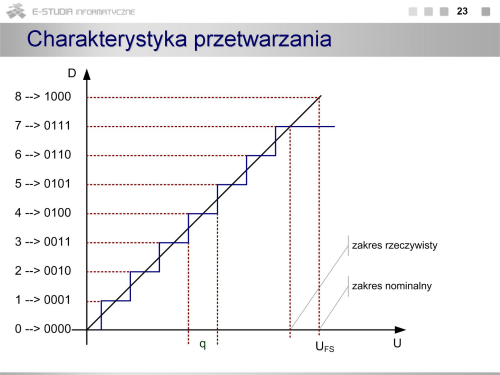
|valign="top"| | |valign="top"|Przykładową charakterystykę dla przetwornika 3-bitowego pokazano na rysunku. | ||
Zakładając, że przetwornik działa w naturalnym kodzie binarnym, wartościom napięcia z przedziału 0¸½q odpowiada stan bitów 000, wartościom ½q ¸ 1½q stan 001. Jeżeli przetwornik jest n-bitowy to może znajdować się w 2n stanach (od 0 do 2n-1). Przejście do maksymalnego stanu (czyli 0111 dla przetwornika 3-bitowego) następuje przy wartości napięcia wejściowego równej UFS - 1½q. Rozróżnia się dwa określenia dotyczące zakresu przetwarzania: nominalny i rzeczywisty zakres przetwarzania. W dokumentacji przetworników jest podawany zakres nominalny, wówczas zakres rzeczywisty (odpowiadający połowie ostatniego schodka) wynosi (UFS – q). Kody cyfrowe, odpowiadające napięciom różniącym się o wartość przedziału kwantowania q, powinny różnić się na pozycji najmniej znaczącego bitu (LSB). Stąd przedział kwantowania jest utożsamiany z najmniej znaczącym bitem i oznaczany jako LSB. Wartość przedziału kwantowania determinuje rozdzielczość przetwornika, z tym, że rozdzielczość jest wyrażana zazwyczaj przez liczbę bitów. W tym ujęciu przetwornik 16-bitowy będzie miał większą rozdzielczość niż przetwornik 10-bitowy. Rozdzielczość można odnieść do wyniku przetwarzania w postaci cyfr dziesiętnych (choć nie jest to dokładna równoważność). Przykładowo przetwornik 10-bitowy może znajdować się w 1024 stanach co odpowiada trzem cyfrom dziesiętnym, a przetwornik 16-bitowy to w dużym przybliżeniu 5 cyfr dziesiętnych. | |||
|} | |} | ||
| Linia 191: | Linia 193: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:UETP_M10_Slajd24.png]] | |valign="top" width="500px"|[[Grafika:UETP_M10_Slajd24.png]] | ||
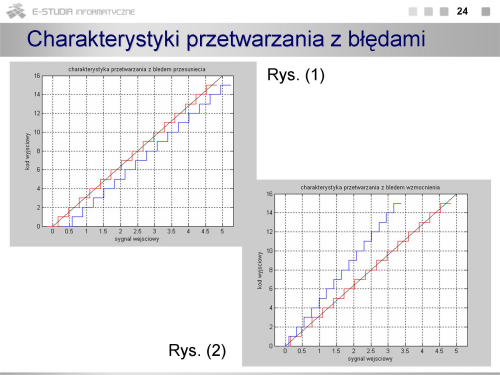
|valign="top"| | |valign="top"|Rzeczywista charakterystyka przetwarzania może mieć przebieg nieco odmienny od przedstawionej właśnie charakterystyki idealnej (dla określonego przedziału kwantowania). Najczęściej można się spotkać z błędami przesunięcia (rys. 1) i wzmocnienia (rys. 2). Oba błędy należą do błędów statycznych oraz systematycznych, zatem mogą być skorygowane w procesie kalibracji przetwornika. | ||
|} | |} | ||
| Linia 198: | Linia 200: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="450px"|[[Grafika:UETP_M10_Slajd25.png]] | |valign="top" width="450px"|[[Grafika:UETP_M10_Slajd25.png]] | ||
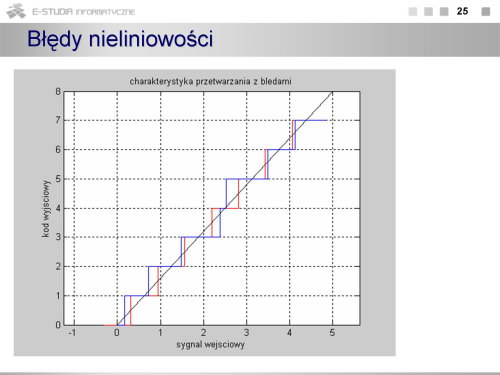
|valign="top"| | |valign="top"|Problem polega na tym, że błędy przetwarzania nakładają się na siebie i ich odseparowanie nie jest proste (kompensacja jednego błędu może powodować zwiększenie innego). Istotne znaczenie mają błędy nieliniowość tzw. nieliniowości całkowej i nieliniowości różniczkowej. Błąd nieliniowości całkowej informuje jakie jest maksymalne odchylenie interpolowanej charakterystyki przetwarzania od charakterystyki idealnej (przy q -> 0) i wyrażany jest w procentach pełnego zakresu przetwarzania UFS. Błąd nieliniowości różniczkowej informuje jaka jest relacja pomiędzy kolejnymi wartościami napięcia wejściowego powodującymi zmianę kodu wyjściowego, a szerokością przedziału kwantowania q. Zauważmy, że jeżeli różnica napięć będzie większa od 2*q to na wyjściu zabraknie jednego kodu, powstanie ważny i niepożądany błąd gubienia kodów. | ||
|} | |} | ||
| Linia 205: | Linia 207: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:UETP_M10_Slajd26.png]] | |valign="top" width="500px"|[[Grafika:UETP_M10_Slajd26.png]] | ||
|valign="top"| | |valign="top"|Dynamiczny zakres przetwarzania jest opisany jako stosunek zakresu przetwarzania do szerokości przedziału kwantowania i wyrażony w decybelach (1). Z zależności tej widać, że dynamika przetwornika zwiększa się o 6dB na 1 bit. | ||
Stosunek wartości skutecznej sygnału do wartości skutecznej szumu kwantyzacji określa współczynnik SNR. Zależność (2) wyraża SNR dla przebiegu sinusoidalnego przy szumie kwantyzacji takim jak na S22 o wartości skutecznej q/sort(12). | |||
|} | |} | ||
| Linia 211: | Linia 215: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:UETP_M10_Slajd27.png]] | |valign="top" width="500px"|[[Grafika:UETP_M10_Slajd27.png]] | ||
|valign="top"| | |valign="top"|Klasyfikacji metod przetwarzania może być wiele, ale w aspekcie zastosowań w technice pomiarowej istotny jest przede wszystkim podział na przetworniki pośrednie i bezpośrednie. W metodach bezpośrednich jest przetwarzana wartość chwilowa napięcia natomiast w większości metod pośrednich - wartość średnia. W kontekście przyrządów i układów pomiarowych podstawowe znaczenie mają: | ||
#metody integracyjne | |||
#metoda bezpośredniego porównania równoległego | |||
#metody wieloprzebiegowe | |||
#metoda kompensacji wagowej | |||
|} | |} | ||
| Linia 218: | Linia 227: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:UETP_M10_Slajd28.png]] | |valign="top" width="500px"|[[Grafika:UETP_M10_Slajd28.png]] | ||
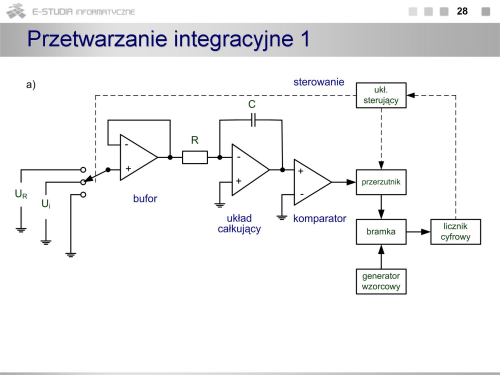
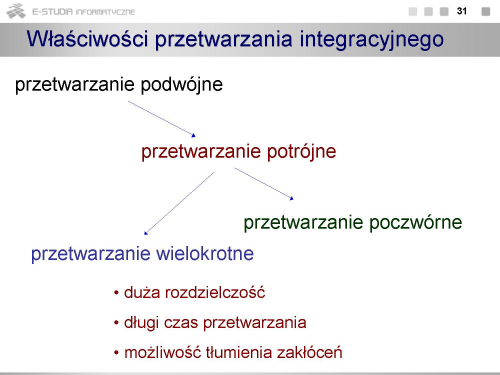
|valign="top"| | |valign="top"|W metodach integracyjnych charakterystyczną cechą jest występowanie procesu całkowania napięcia przetwarzanego przez ładowanie lub rozładowanie kondensatora w układzie RC. Proces całkowania jest realizowany na pewnym odcinku czasu, a sygnał wyjściowy jest proporcjonalny do wartości średniej napięcia wyjściowego w okresie integracji. Uśrednianie napięcia jest jedną z podstawowych zalet tej metody ze względu na możliwość skutecznej eliminacji (przez uśrednianie) zakłóceń nakładających się na przetwarzany sygnał. Drugą ważną cechą jest rozdzielczość i dokładność przetwarzania szczególnie przy stosowaniu całkowania wielokrotnego. Metody integracyjne są powszechnie stosowane w multimetrach cyfrowych (od prostych multimetrów przenośnych do precyzyjnych multimetrów laboratoryjnych), w których dokładność przetwarzania jest ważniejsza od szybkości rejestracji sygnałów. | ||
|} | |} | ||
| Linia 224: | Linia 233: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:UETP_M10_Slajd29.png]] | |valign="top" width="500px"|[[Grafika:UETP_M10_Slajd29.png]] | ||
|valign="top"| | |valign="top"|W pierwszej fazie przetwarzania jest całkowane napięcie wejściowe Ui w ściśle określonym czasie T1. | ||
Po czasie T1 napięcie U na kondensatorze jest proporcjonalne do średniej wartości napięcia wejściowego w czasie całkowania (1). W drugiej fazie przetwarzania kondensator jest rozładowywany prądem ze źródła napięcia UR o polaryzacji przeciwnej do napięcia wejściowego. Po czasie T2 napięcie na kondensatorze spada do 0 (2). | |||
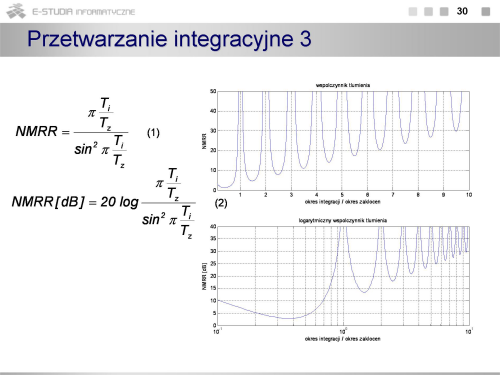
Z zależności (4) widać, że czas T2 nie zależy od wartości RC, zatem parametry tego układu nie mają istotnego wpływu na wyznaczoną wartość odstępu czasu (choć mogą stanowić źródło błędów przetwarzania). | |||
Jeżeli czas T1 i T2 są mierzone cyfrowo przy wykorzystaniu tego samego generatora wzorcowego to również dokładna wartość okresu tego generatora nie ma wpływu na wynik przetwarzania w postaci liczby impulsów zliczonych w czasie T2 . | |||
|} | |} | ||
Wersja z 16:59, 28 wrz 2006
wersja beta
Moduł 10 - Przetwarzanie wielkości elektrycznych

|

|
Sygnały pomiarowe
|
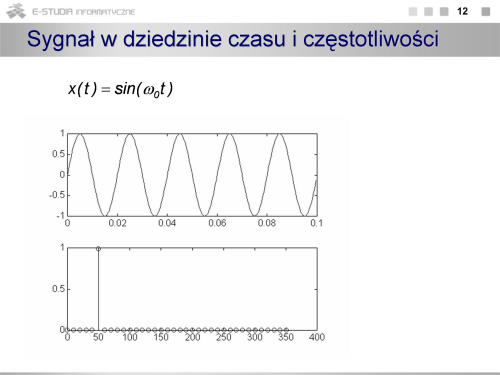
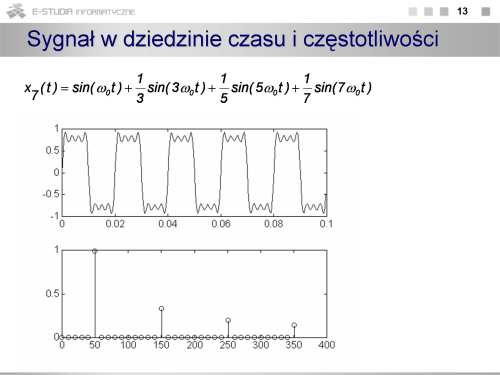
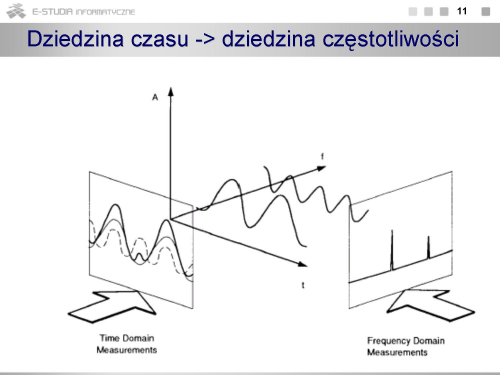
Na rysunku przedstawiono poglądowo obraz sygnału w dziedzinie częstotliwości. Stanowią go prążki o wysokości odpowiadającej wartości harmonicznych. |
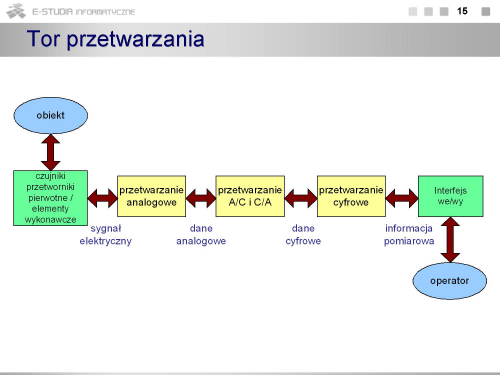
Tor przetwarzania sygnałów
Przetwarzanie analogowo-cyfrowe
|
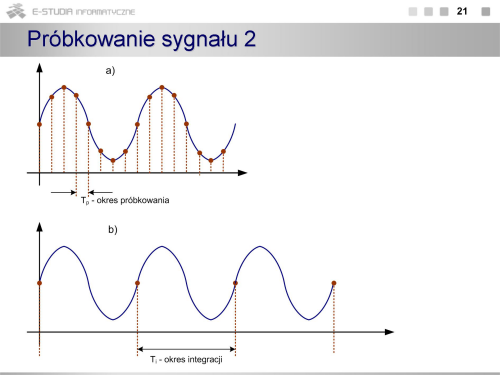
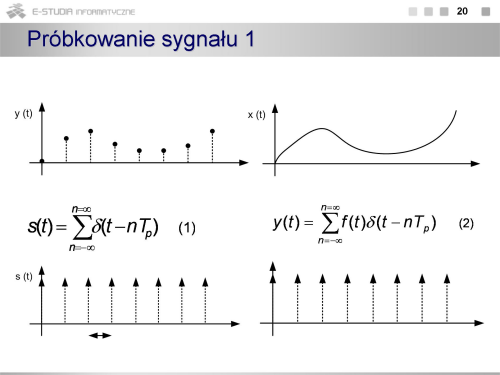
Matematycznie próbkowanie można interpretować jak mnożenie sygnału ciągłego x(t) przez funkcję próbkującą s(t) w postaci impulsów Diraca (1).
|
|
|
|
|

|
|

|
|

|
|
|