Układy elektroniczne i technika pomiarowa/Moduł 10

wersja beta

---

Moduł 10 - Przetwarzanie wielkości elektrycznych

---

---

Sygnały pomiarowe

Pozyskana w wyniku pomiaru informacja wymaga zazwyczaj przesłania, zapamiętania lub dalszego przetworzenia. Nośnikiem informacji może być dowolna wielkość elektryczna, której wartość zmienia się pod wpływem badanego zjawiska fizycznego. Z uwagi na to, że wszelkim zjawiskom i procesom towarzyszy upływ czasu, stąd fundamentalne znaczenie w technice pomiarowej ma pojęcie sygnału pomiarowego, którego parametr jest nośnikiem informacji. Elementarny podział sygnałów obejmuje sygnały zdeterminowane tzn. opisane równaniami analitycznymi, których wartości możemy na podstawie tych równań wyznaczyć i sygnały losowe (stochastyczne) tzn. takie, których parametry możemy co najwyżej oszacować korzystając metod probabilistycznych.

---

Podstawowe znaczenie ma sygnał harmoniczny (omawiany w …..oraz……). Znaczenie tego sygnału przejawia się w tym, że jest to sygnał, jaki występuje w sieci energetycznej, z której zasilane są urządzenia techniczne. Zauważmy, że różnego typu zjawiska i procesy mogą powodować zmiany parametrów sygnału, powodując, że parametry stają się nośnikami informacji. Ponadto sygnały harmoniczne (sinus i cosinus) stanowią jedną z baz sygnałów ortogonalnych umożliwiając analizę sygnałów złożonych (rozłożenie na elementy składowe). Szczególne znaczenie ma okresowość sygnałów oznaczająca powtarzalność wartości parametrów z interwałem czasowym (okresem).

---

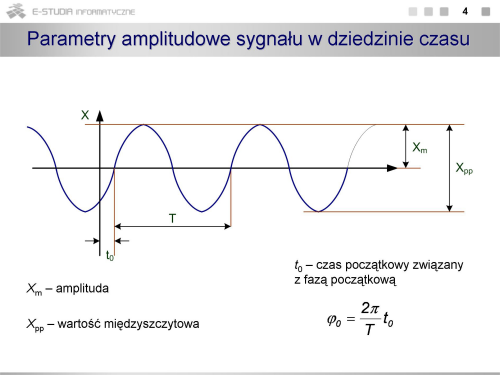
Przebieg sygnału opisanego równaniem (1s3) pokazano na rysunku modyfikując oznaczenia na często spotykane przy charakteryzowaniu parametrów przebiegów elektrycznych. Zauważmy, że wartości minimalna i maksymalna sygnału są równe, co do wartości bezwzględnych, i zgodne z amplitudą sygnału.

---

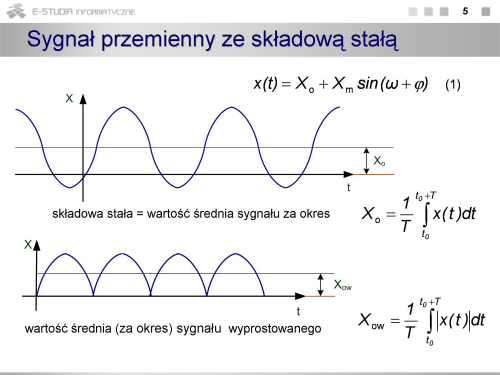
W rzeczywistości tak być nie musi i wartości minimalna i maksymalną mogą być różne. Wówczas mówimy, że sygnał ma składową stałą. Przy czy określenie amplituda nadal jednoznacznie definiuje największą, co do wartości bezwzględnej wartość sygnału bez składowej stałej. Oczywiście dla sygnału opisanego zależnością (1s3) wartość stała jest równa 0. Z powodów praktycznych definiuje się również pojęcie wartości średniej sygnału wyprostowanego, która jest różna od 0.

---

Najważniejszym parametrem sygnału jest jednak jego wartość skuteczna. Opisowo można wyjaśnić, że wartość skuteczna sygnału przemiennego jest równa wartości sygnału stałego, który powoduje takie same skutki energetyczne jak sygnał przemienny. Zatem wartość skuteczna jest „miarą mocy” sygnału, stąd jej podstawowe znaczenie. Wszystkie przyrządy pomiarowe przy włączonej funkcji pomiaru parametrów sygnału zmiennego pokazują właśnie wartość skuteczną. Problem interpretacji wskazań przyrządów pomiarowych jest bardzo istotny, chodzi przecież o odpowiedź na pytanie – co mierzy przyrząd ?. Kontrowersje wzbudza tak prozaiczny problem jak wartość skuteczna sygnału ze składową stałą. Zależność (2) opisuje tą wartość jako złożenie dwóch wartości: składowej stałej i wartości skutecznej składowej przemiennej. Z kolej zależność (3) wyraża stosunek amplitudy do wartości skutecznej i jest ważnym parametrem określającym „strzelistość” (ostrość sygnału). Z reguły przetworniki mają ograniczoną możliwość przetwarzania sygnałów w postaci wąskich impulsów, których współczynnik szczytu jest duży (np. większy od 10).

---

Wartość skuteczna sygnału może być wyznaczona z zależności (5). Uzasadnieniem tego wzoru jest równoważność energetyczna sygnału przemiennego i stałego. Moc chwilowa jest opisana wzorem (1) jako iloczyn chwilowych wartości prądu i napięcia. Moc czynna (2) jest wartością średnią mocy chwilowej za okres. Z równania (4) wyrażającego moc wydzieloną na rezystancji R przy przepływie prądu zmiennego i stałego wynika właśnie zależność (5).

---

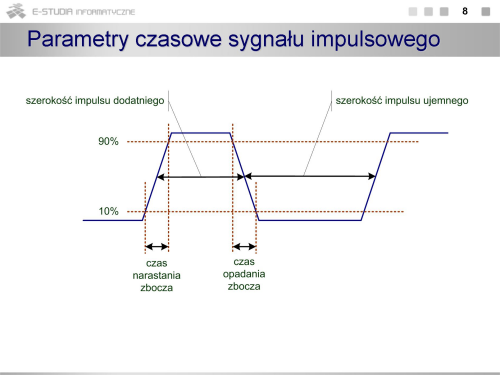
Dla sygnału harmonicznego o kształcie sinusoidalnym podstawowym parametrem czasowym jest okres i jego odwrotność, czyli częstotliwość. W przypadku przebiegów o charakterze impulsowym istotne znaczenie mają parametry takie jak czasy trwania dodatniej lub ujemnej części impulsu czy czasy narastania i opadania zboczy. Oczywiście wielkości takie mogą być badane również dla sygnałów sinusoidalnych, ale ich znaczenie jest większe dla sygnałów impulsowych. W szczególności ważnym parametrem może być stosunek czasu trwania wysokiego poziomu sygnału do okresu nazywany współczynnikiem wypełnienia. Pomiary parametrów czasowych sygnałów mają o tyle znaczenie, że mogą być wykonywane z dużą dokładnością, znacznie większą niż parametry amplitudowe.

---

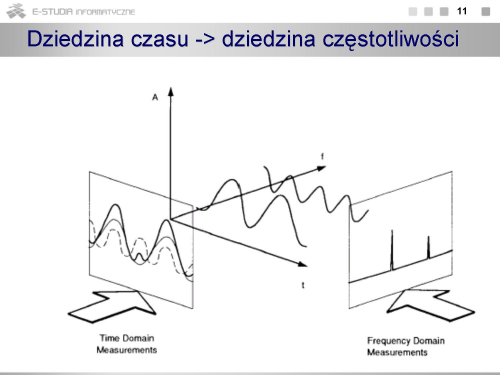
Podawane dotychczas parametry opisują sygnały w dziedzinie czasu. Alternatywnie można sygnały przedstawiać w dziedzinie częstotliwości. Badanie własności sygnałów w dziedzinie częstotliwości określa się mianem analizy widmowej. Przejście z dziedziny czasu do dziedziny częstotliwości jest matematycznie opisane przez całkowe przekształcenie Fouriera (1), a odtworzenie sygnału w dziedzinie czasu jest możliwe przy wykorzystaniu transformaty odwrotnej (2).

---

Jeżeli sygnał w dziedzinie czasu jest okresowy to można go przedstawić w postaci sumy funkcji trygonometrycznych (szeregu Fouriera) (1). Z zależności tej wynika, że sygnał okresowy można „rozłożyć” na elementy składowe w postaci składowych harmonicznych o różnych amplitudach. Częstotliwości harmonicznych są wielokrotnościami częstotliwości podstawowej. Taki proces analizy podlega różnym warunkom matematycznym, co jest przedmiotem wykładu z Teorii Sygnałów. W aspekcie techniki pomiarowej istotne jest to, że wiele zjawisk czy też właściwości obiektów są lepiej identyfikowalne w dziedzinie częstotliwości niż czasu. Spektakularnym przykładem jest tutaj problem jakości energii elektrycznej, a konkretnie zniekształceń napięcia w sieci energetycznej.

---

---

---

---

---

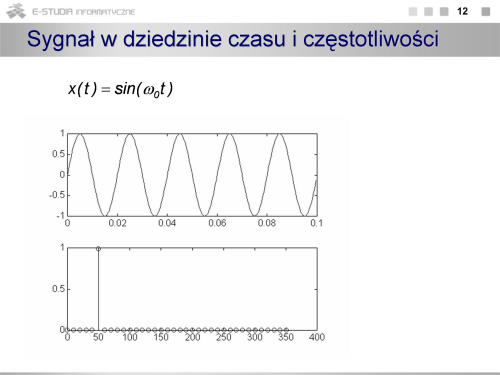
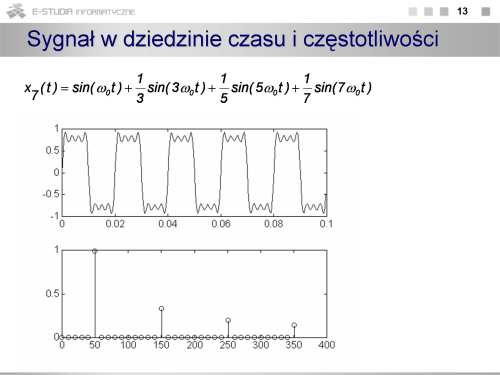
Tor przetwarzania sygnałów

---

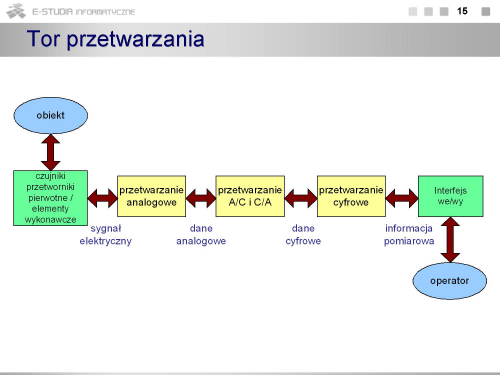
Plik:UETP M10 Slajd16.png

---

Plik:UETP M10 Slajd17.png

---

Plik:UETP M10 Slajd18.png

---

Przetwarzanie analogowo-cyfrowe

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---
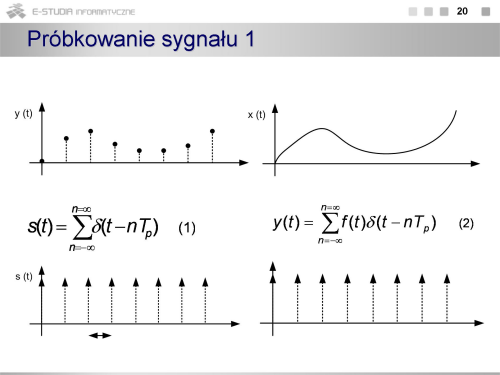
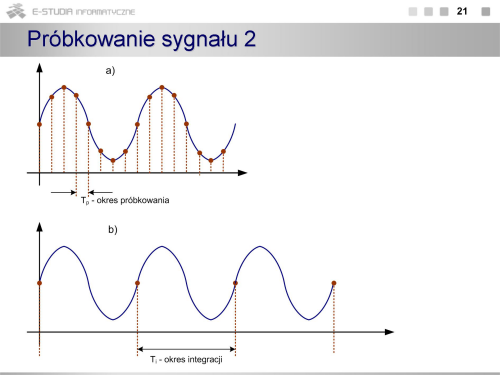
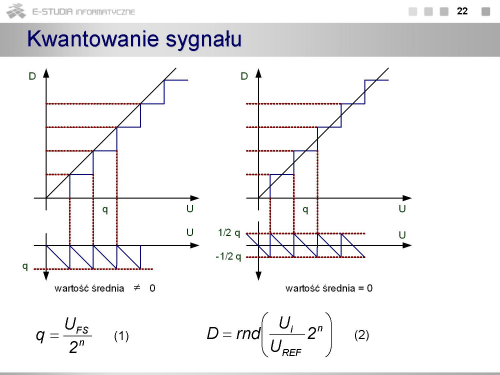
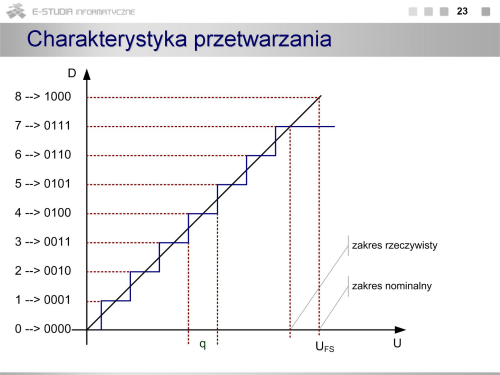
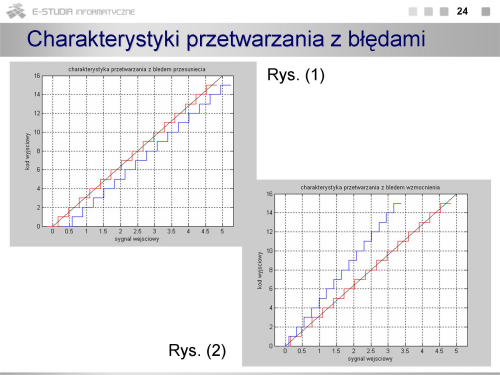
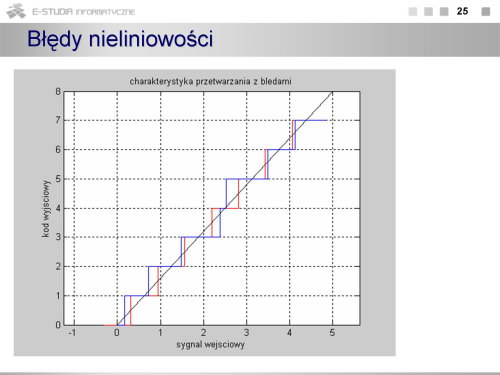
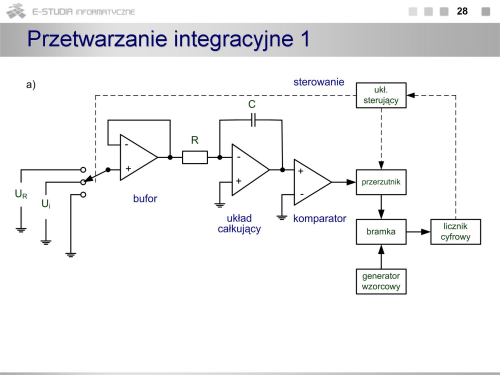
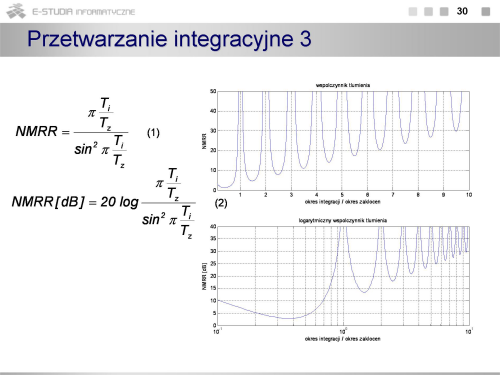
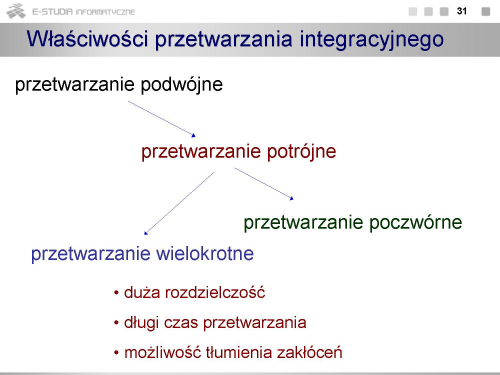
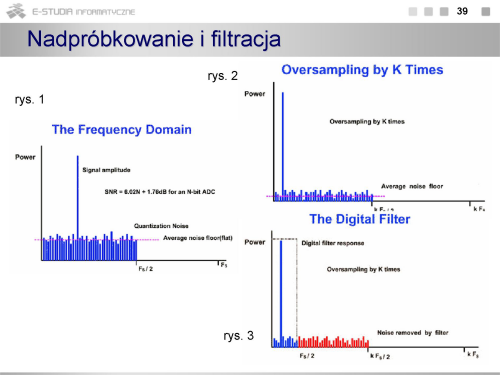
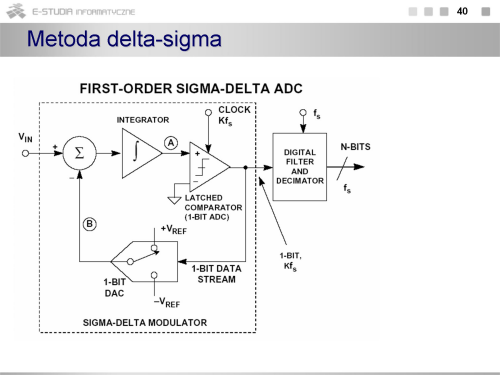