Układy elektroniczne i technika pomiarowa/Moduł 2

wersja beta

---

Moduł 2 - Sprzężenie zwrotne

Wykład 2. Sprzężenie zwrotne

---

Wstęp Koncepcję sprzężenia zwrotnego, w latach trzydziestych dwudziestego wieku, opublikował H. S. Black i obecnie jest ono (sprzężenie zwrotne) powszechnie stosowne w analogowych układach elektronicznych. W niniejszym module opisano podstawowe elementy teorii sprzężenia zwrotnego. Wprowadzono klasyfikację sprzężeń zwrotnych oraz omówiono podstawowe pojęcia związane z opisem sygnałów i ich transmisją w analogowych układach elektronicznych. Przedstawiono także wpływ sprzężenia zwrotnego na podstawowe parametry układu elektronicznego, takie jak: wzmocnienie, impedancję wejściową i wyjściową, charakterystyki częstotliwościowe, zakłócenia i szumy oraz stabilność i liniowość.

---

Słowniczek sprzężenie zwrotne – transmisja całego lub części sygnału wyjściowego w układzie elektronicznym i po zsumowaniu z sygnałem sterującym ponowne zadanie go na wejście układu stopień sprzężenia zwrotnego lub współczynnik redukcji wzmocnienia – wyrażenie, jeden minus wzmocnienie pętli sprzężenia zwrotnego, występujące w mianowniku transmitancji układu zamkniętego

---

sygnał sprzężenia zwrotnego – sygnał wyjściowy czwórnika sprzężenia zwrotnego, który jest sumowany z sygnałem sterującym układ elektroniczny transmitancja czwórnika sprzężenia zwrotnego – transmitancja widmowa układu liniowego, szczególny przypadek transmitancji operatorowej układu liniowego. Jest to stosunek sygnałów harmonicznych wyjściowego do wejściowego czwórnika sprzężenia zwrotnego zapisanych w postaci liczb zespolonych transmitancja układu otwartego - transmitancja widmowa układu liniowego, szczególny przypadek transmitancji operatorowej układu liniowego. Jest to stosunek sygnałów harmonicznych wyjściowego do wejściowego układu elektronicznego ( np. wzmacniacza) zapisanych w postaci liczb zespolonych

---

układ regulacji automatycznej – układ sterowania, w którym zastosowano sprzężenie zwrotne, układ zamknięty układ zamknięty – układ ze sprzężeniem zwrotnym wzmocnienie pętli sprzężenia zwrotnego – moduł iloczynu transmitancji widmowej układu otwartego i transmitancji widmowej czwórnika sprzężenia zwrotnego

---

Pojęcia podstawowe Termin sprzężenie zwrotne jest związany z teorią transmisji sygnałów i oznacza, że napięcie wyjściowe dowolnego liniowego układu analogowego, np. wzmacniacza akustycznego, w odpowiedniej proporcji oraz w miarę potrzeby odpowiednio odfiltrowane ponownie jest kierowane do wejścia wzmacniacza i dodaje się lub odejmuje się od sygnału sterującego. Kiedy sygnał sprzężenia zwrotnego odejmuje się od sygnału sterującego wzmacniacz, występuje sprzężenie zwrotne ujemne. Jeżeli sygnały sterujący i sprzężenia zwrotnego dodają się, występuje sprzężenie zwrotne dodatnie.

---

Podobnie jak w układach regulacji automatycznej gdzie bloki są opisane transmitancją widmową tak i poszczególne fragmenty lub całe układy elektroniczne można traktować jak czwórniki i także można je opisać odpowiednią transmitancją widmową np. $K(j\omega ),\beta (j\omega )$.

---

---

Weźmy pod uwagę schemat blokowy układu przedstawiony na rysunku. Układ składa się z dwóch czwórników o transmitancjach: $K(j\omega )$ – dla czwórnika wzmacniacza, $\beta (j\omega )$ – dla czwórnika sprzężenia zwrotnego. Ponieważ w ogólnym wypadku transmitancje widmowe obu czwórników zależą od częstotliwości dlatego są funkcjami zmiennych zespolonych. Transmitancję widmową $K(j\omega )$ nazywamy transmitancją układu otwartego, a transmitancję widmową $\beta (j\omega )$ transmitancją czwórnika sprzężenia zwrotnego. Przyjmując oznaczenia: $X(j\omega )$ – sygnał sterujący, $X_s(j\omega )$ – sygnał wyjściowy czwórnika sprzężenia zwrotnego, $X_i(j\omega )$ – sygnał wejściowy czwórnika wzmacniacza, $Y(j\omega )$ – sygnał wyjściowy, który jest jednocześnie sygnałem wejściowym czwórnika sprzężenia zwrotnego, przedstawiony na rysunku schemat można opisać równaniami: $K(j\omega )=\frac{Y(j\omega )}{X_i(j\omega )}$ 2.1 $\beta (j\omega )=\frac{X_s(j\omega )}{Y(j\omega )}$ 2.2 Łatwo zauważyć, że dla sprzężenia zwrotnego ujemnego $X(j\omega )-X_s(j\omega )=X_i(j\omega )$ 2.3 a dla sprzężenia zwrotnego dodatniego $X(j\omega )+X_s(j\omega )=X_i(j\omega )$ 2.4

---

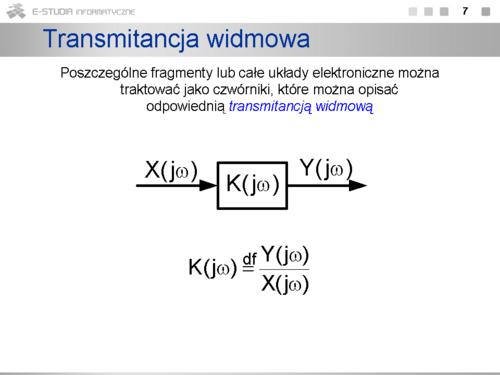
Transmitancja układu ze sprzężeniem zwrotnym $K_z(j\omega )$, zwanego krótko układem zamkniętym, uwzględniając zależności 2.1, 2.2, oraz 2.3. lub 2.4, jest opisana zależnością: Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle K_z(j\omega)= \frac{Y(j\omega)}{X(j\omega)}=\frac{K(j\omega)}{1-K(j\omega)\cdot \beta(j\omega)}}} 2.5 Ponieważ czwórnik sprzężenia zwrotnego najczęściej spełnia zależność $\beta (j\omega )>0$ (sprzężenie nie odwraca fazy sygnału), aby zrealizować ujemne sprzężenie zwrotne, czwórnik wzmacniacza powinien spełnić zależność $K(j\omega )<0$ (odwraca fazę), a dla sprzężenia zwrotnego dodatniego $K(j\omega )>0$ (nie odwraca fazy).

---

Iloczyn $|K(j\omega )\cdot \beta (j\omega )|$ jest nazywany wzmocnieniem pętli sprzężenia zwrotnego. Jeżeli wzmocnienie pętli jest duże mówimy, że w układzie zastosowano silne sprzężenie zwrotne. Dołączenie czwórnika sprzężenia zwrotnego zmienia wzmocnienie układu otwartego. W zależności od warunku jaki spełnia wyrażenie $1-K(j\omega )\cdot \beta (j\omega )$ można wyróżnić trzy podstawowe skutki działania sprzężenia zwrotnego:

---

$\begin{array}{ccc}Przypadek1.& |1-K(j\omega )\cdot \beta (j\omega )|>1;& |K_z(j\omega )|<|K(j\omega )|\end{array}$ 2.6 W układzie występuje ujemne sprzężenie zwrotne. Wzmocnienia w układzie zamkniętym w stosunku do wzmocnienia jakie było w układzie otwartym zmniejsza się.

---

$\begin{array}{ccc}Przypadek2.& |1-K(j\omega )\cdot \beta (j\omega )|>1;& |K_z(j\omega )|>|K(j\omega )|\end{array}$ 2.7 W układzie występuje dodatnie sprzężenie zwrotne, które powoduje w układzie zamkniętym zwiększenie wzmocnienia w stosunku do wzmocnienia jakie było w układzie otwartym.

---

$\begin{array}{ccc}Przypadek3.& |1-K(j\omega )\cdot \beta (j\omega )|=0;& |K_z(j\omega )|\to \mathrm{\infty }\end{array}$ 2.8 Dodatnie sprzężenie zwrotne jest tak silne, że możliwa jest praca układu zamkniętego bez zewnętrznego sygnału sterującego. W układach elektronicznych wykorzystuje się wszystkie trzy wyżej wymienione przypadki. Pierwszy jest stosowany we wzmacniaczach głównie w celu poprawy ich parametrów eksploatacyjnych. W przypadku układów ze wzmacniaczami operacyjnymi wzmocnieniem pętli sprzężenia zwrotnego jest bardzo duże. Oznacza to, że oddziaływanie pętli sprzężenia zwrotnego jest tak silne, że o właściwościach statycznych i dynamicznych układu zamkniętego decydują wyłącznie elementy z jakich jest zbudowana pętla sprzężenia zwrotnego. Do budowy tej pętli stosuje się elementy pasywne (np. kondensator i rezystory) o stabilnych parametrach nie wrażliwych np. na zmianę temperatury. Drugi przypadek jest powszechnie stosowany w układach przełączających, głównie w technice cyfrowej, w których pętla sprzężenia zwrotnego działa forsująco, powodując szybką zmianę stanu łączników elektronicznych. Umożliwia to uzyskanie sygnałów impulsowych o dużej stromości narastania i opadania. Trzeci przypadek występuje w układach generatorów drgań sinusoidalnych z pętlą sprzężenia zwrotnego.

---

Klasyfikacja sprzężeń zwrotnych Podstawowy podział sprzężeń zwrotnych to podział na sprzężenie zwrotne dodatnie i sprzężenie zwrotne ujemne. Tę cechę należy bezwzględnie podać, aby ocenić właściwości układu z punktu widzenia transmisji i przetwarzania sygnałów. Ponad to sprzężenia zwrotne dzielimy: ze względu na sposób wprowadzenia sygnału sprzężenia zwrotnego na wejście wzmacniacza na sprzężenie zwrotne szeregowe i sprzężenie zwrotne równoległe, ze względu na sposób próbkowania (pomiaru) sygnału sprzężenia zwrotnego na wyjściu wzmacniacza na sprzężenie zwrotne prądowe i sprzężenie zwrotne napięciowe, ze względu na kształt charakterystyki częstotliwościowej czwórnika sprzężenia zwrotnego na sprzężenie zwrotne selektywne i sprzężenie zwrotne liniowe (nieselektywne). ze względu na liczbę czwórników (stopni wzmacniających) w torze wzmacniacza na sprzężenie zwrotne jednostopniowe i sprzężenie zwrotne wielostopniowe, ze względu na rodzaj zastosowanych do budowy pętli sprzężenia zwrotnego elementów na sprzężenie zwrotne pasywne i sprzężenie zwrotne aktywne.

---

Sprzężenie zwrotne: a) szeregowe, b) równoległe c) napięciowe, d) prądowe Te cechy sprzężenia zwrotnego (szeregowe czy równoległe, napięciowe czy prądowe) należy bezwzględnie podać, jeżeli chcemy dokładnie określić, z punktu widzenia transmisji sygnałów, rodzaj zastosowanego w układzie sprzężenia zwrotnego i jednoznacznie opisać skutki jego zastosowania.

---

Przykłady realizacji rzeczywistych układów ze sprzężeniem zwrotnym. Proste przykłady zastosowania ujemnego sprzężenia zwrotnego: a) sprzężenie napięciowe-równoległe, b) sprzężenie prądowe-szeregowe.

---

W zależności od rodzaju zastosowanego sprzężenia zwrotnego poszczególne transmitancje widmowe $K(j\omega )$ i $\beta (j\omega )$ maja różną postać, stosownie do tego, jakie sygnały są rozważane na wejściu i na wyjściu układu. Dla sprzężenia napięciowego-szeregowego $\begin{array}{cc}K(j\omega )=\frac{U(j\omega )}{U_i(j\omega )}=K_u(j\omega );& \beta (j\omega )=\frac{U_s(j\omega )}{U(j\omega )}={\beta }_u(j\omega )\end{array}$ 2.9 Dla sprzężenia napięciowego-równoległego $\begin{array}{cc}K(j\omega )=\frac{U(j\omega )}{I_i(j\omega )}=K_{ui}(j\omega );& \beta (j\omega )=\frac{I_s(j\omega )}{U(j\omega )}={\beta }_{iu}(j\omega )\end{array}$ 2.10 Dla sprzężenia prądowego-szeregowego $\begin{array}{cc}K(j\omega )=\frac{I(j\omega )}{U_i(j\omega )}=K_{iu}(j\omega );& \beta (j\omega )=\frac{U_s(j\omega )}{I(j\omega )}={\beta }_{ui}(j\omega )\end{array}$ 2.11 Dla sprzężenia prądowego-równoległego $\begin{array}{cc}K(j\omega )=\frac{I(j\omega )}{I_i(j\omega )}=K_i(j\omega );& \beta (j\omega )=\frac{I_s(j\omega )}{I(j\omega )}={\beta }_i(j\omega )\end{array}$ 2.12

---

Topologie idealnych czwórników stosowanych w pętli sprzężenia zwrotnego: a) dla sprzężenia napięciowego-szeregowego, b) dla sprzężenia napięciowego-równoległego c) dla sprzężenia prądowego-szeregowego, d) dla sprzężenia prądowego-równoległego. Zależność opisująca transmitancję układu zamkniętego jest prawdziwa tylko dla tych transmitancji, które odpowiadają kombinacji sygnałów wejściowych i wyjściowych konkretnego rodzaju sprzężenia zwrotnego. Jeżeli np. sprzężenie jest prądowe-szeregowe to transmitancje widmowe $K(j\omega )$ i $K_z(j\omega )$ są transmitancjami prądowo-napięciowymi $K_{iu}(j\omega )$ i $K_{ziu}(j\omega )$ i nie można wnioskować na ich podstawie jakie są wzmocnienia napięciowe $K_u(j\omega )$ i $K_{zu}(j\omega )$ lub prądowe $K_i(j\omega )$ i $K_{zi}(j\omega )$.

---

Wpływ ujemnego sprzężenia zwrotnego na właściwości wzmacniacza Wzmocnienie W układzie z ujemnym sprzężeniem zwrotnym zawsze odpowiednie wzmocnienie układu zamkniętego $K_{zu}(j\omega ),K_{ziu}(j\omega ),K_{zui}(j\omega ),K_{zi}(j\omega )$ jest mniejsze od wzmocnienia w układzie otwartym $K_u(j\omega ),K_{iu}(j\omega ),K_{ui}(j\omega ),K_i(j\omega )$ . Impedancja wejściowa Jeżeli zastosowane sprzężenie zwrotne jest szeregowe to impedancja wejściowa układu zamkniętego rośnie, jeśli równoległe zmniejsza się. Odpowiednie zmiany wynikają z połączenia impedancji wejściowej wzmacniacza i impedancji wyjściowej czwórnika sprzężenia zwrotnego. W przypadku sprzężenia szeregowego impedancje dodają się. Przy sprzężeniu równoległym są połączone równolegle. Impedancja wyjściowa Jeżeli zastosowane sprzężenie zwrotne jest prądowe to impedancja wyjściowa układu zamkniętego rośnie, a jeśli napięciowe zmniejsza się. W przypadku sprzężenia prądowego impedancja wyjściowa układu zamkniętego jest sumą impedancji wyjściowej wzmacniacza i wejściowej czwórnika sprzężenia zwrotnego. Przy sprzężeniu napięciowym obie impedancje są połączone równolegle. W tabeli przedstawiono wpływ ujemnego sprzężenia zwrotnego na parametry robocze wzmacniacza. We wszystkich przypadkach zmiany są proporcjonalne do współczynnika $k=|1-K(j\omega )\cdot \beta (j\omega )|$ zwanego stopniem sprzężenia zwrotnego lub współczynnikiem redukcji wzmocnienia.

---

Liniowość układu Z zasady działania ujemnego sprzężenia zwrotnego wynika, że dzięki porównaniu sygnału sterującego wzmacniacz $X(j\omega )$ z próbką sygnału wyjściowego $X_s(j\omega )$ powstaje mały sygnał uchybu $X_i(j\omega )$ sterujący wejściem wzmacniacza, który jest tym mniejszy im większe wzmocnienie pętli sprzężenia zwrotnego. Zatem, jeżeli wzmacniacz bez sprzężenia zwrotnego jest nieliniowy to w wyniku działania ujemnego sprzężenia zwrotnego w znacznym stopniu ograniczony zostaje zakres zmian sygnału $X_i(j\omega )$, i dzięki temu powstałe zniekształcenia sygnału wyjściowego będą częściowo skompensowane. Zatem w przypadku bardzo silnego sprzężenia zwrotnego linearyzacja charakterystyki przenoszenia układu będzie bardzo skuteczna. Działanie linearyzujące ujemnego sprzężenia zwrotnego w układzie wzmacniacza przedstawiono na rysunku.

---

Zakłócenia i szumy Na slajdzie 22 przedstawiono schemat blokowy układu ze sprzężeniem zwrotnym, w którym uwzględniono sygnały zakłócające. Sygnały zakłócające $X_{z1}(j\omega )$, w tym także szumy, które są zawarte w sygnale wejściowym dodają się do sygnału użytecznego $X(j\omega )$ i są identycznie jak ten sygnał i są identycznie wzmacniane. Zatem zastosowanie sprzężenia zwrotnego nie poprawi w tym wypadku stosunku sygnału do szumów. Co więcej, ponieważ obwód sprzężenia zwrotnego jest zbudowany z elementów, które z natury są źródłem dodatkowych szumów (zwykle rezystorów), wartość współczynnika szumów układu ze sprzężeniem zwrotnym będzie zazwyczaj większa niż w układzie otwartym. W praktyce w prawidłowo zrealizowanej pętli sprzężenia zwrotnego przyrost ten powinien być niewielki. Jeżeli sygnały zakłóceń $X_{z2}(j\omega ),X_{z3}(j\omega ),X_{z4}(j\omega ),$ są wprowadzane na wejścia dalszych stopni wzmacniacza układ ze sprzężeniem zwrotnym tłumi je tym bardziej im bliżej wyjścia znajduje się ich źródło. Wynika to z analizy zależności opisującej sygnał wyjściowy w układzie ze slajdu 22: $Y(j\omega )=\frac{[X(j\omega )+X_{z1}(j\omega )+X_{z2}(j\omega )]\cdot K_1(j\omega )\cdot K_2(j\omega )}{1-\beta (j\omega )\cdot K_1(j\omega )\cdot K_2(j\omega )}+$ $+\frac{X_{z3}(j\omega )\cdot K_2(j\omega )}{1-\beta (j\omega )\cdot K_1(j\omega )\cdot K_2(j\omega )}+\frac{X_{z4}(j\omega )}{1-\beta (j\omega )\cdot K_1(j\omega )\cdot K_2(j\omega )}$ 2.13 Sygnał zakłócający $X_{z4}(j\omega )$ działający na stopień wyjściowy jest najbardziej tłumiony. Jest to szczególnie korzystne w układach wzmacniaczy mocy, w których stopnie końcowe zasila się z niestabilizowanego źródła napięcia stałego o dość dużej zawartości tętnień.

---

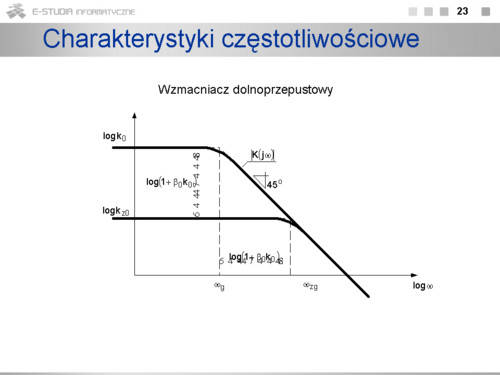Charakterystyki częstotliwościowe Wpływ sprzężenia zwrotnego na charakterystyki częstotliwościowe układu zamkniętego zależy od przebiegu tych charakterystyk w układzie bez sprzężenia. W najprostszym przypadku zakłada się, że wzmacniacz jest opisany transmitancją widmową układu dolnoprzepustowego pierwszego rzędu: :$K(j\omega )=\frac{K_0}{1+j\frac{\omega }{{\omega }_g}}$ 2.14 gdzie $K_0(K_0<0)$ wzmocnienie wzmacniacza odwracającego fazę dla niskich częstotliwości, a Parser nie mógł rozpoznać (błąd składni): {\displaystyle ω_g\,} górna graniczna pulsacja wzmacniacza oraz transmitancja widmowa pętli sprzężenia zwrotnego nie zależy od częstotliwości i jest opisana zależnością: $\beta (j\omega )={\beta }_0({\beta }_0>0)$ 2.15 Transmitancja widmowa układu zamkniętego ma postać: :$K_z(j\omega )=\frac{K_{z0}}{1+j\frac{\omega }{{\omega }_{gz}}}$ 2.16 gdzie $K_{z0}=\frac{K_0}{1-\beta K_0}$ wzmocnienie układu w zakresie niskich częstotliwości, a ${\omega }_{gz}={\omega }_g(1-\beta K_0)$ górna graniczna pulsacja wzmacniacza objętego sprzężeniem zwrotnym. Ujemne sprzężenie zwrotne powoduje zwiększenie górnej częstotliwości granicznej wzmacniacza proporcjonalnie do współczynnika redukcji wzmocnienia dla niskich częstotliwości. Iloczyn wzmocnienia Parser nie mógł rozpoznać (błąd składni): {\displaystyle │K_0│\,} i częstotliwości $f_g$ nazywamy polem wzmocnienia i jest dla układów o transmitancji widmowej opisanej zależnością 2.14 stała: $|K_0|\cdot f_g=|K_{z0}|\cdot f_{gz}=const$ Do podobnych wniosków prowadzi analiza wzmacniacza, który jest opisany transmitancją widmową układu górnoprzepustowego pierwszego rzędu: :$K(j\omega )=\frac{K_0}{1+\frac{{\omega }_d}{j\omega }}$ 2.17 gdzie $K_0(K_0<0)$ wzmocnienie wzmacniacza dla wysokich częstotliwości, a ${\omega }_d$ dolna graniczna pulsacja wzmacniacza. Przyjmując, że transmitancja widmowa pętli sprzężenia zwrotnego nie zależy od częstotliwości, transmitancja widmowa układu zamkniętego ma postać: :$K_{z0}(j\omega )=\frac{K_{z0}}{1+\frac{{\omega }_{dz}}{j\omega }}$ 2.18 gdzie $K_{z0}=\frac{K_0}{1-\beta K_0}$ wzmocnienie układu w zakresie wysokich częstotliwości, a $\omega dz=\frac{{\omega }_d}{1-\beta K_0}$ dolna graniczna pulsacja wzmacniacza objętego sprzężeniem zwrotnym. W zakresie niskich częstotliwości pasmo przenoszenia rozszerza się proporcjonalnie do współczynnika redukcji wzmocnienia.

---

Stabilność Wraz ze wzrostem liczby stopni wzmacniacza objętych pętlą sprzężenia zwrotnego może w pętli sprzężenia zwrotnego wystąpić tak duże przesunięcie fazy, że zmieni się charakter sprzężenia z ujemnego na dodatnie, a to w konsekwencji spowoduje generację drgań i uniemożliwi prawidłową pracę wzmacniacza.

---

Podsumowanie Ujemne sprzężenie zwrotne powoduje w układzie elektronicznym: poprawę liniowości charakterystyki przenoszenia, poszerzenie pasma przenoszenia, modyfikację impedancji wejściowej i wyjściowej, zmniejszenie wrażliwość układu na zakłócenia, np. pochodzące z sieci zasilającej (przydźwięk), zmniejszenie wpływu zmian parametrów zasilania i elementów układu, głównie parametrów tranzystorów na wzmocnienie, stabilizację punkty pracy tranzystorów, zwiększenie stabilność pracy, oraz umożliwia kształtowanie charakterystyki częstotliwościowej układu.

---

Bibliografia

1. Black H. S.: Stabilized feedback amplifiers. Electrical Engineering, Vol. 53,

January 1934, s. 114-120.

1. Kaźmierkowski M. P., Matysik J. T.: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 2005
2. Baranowski J., Nosal Z.: Układy elektroniczne cz. I. Układy analogowe liniowe, Wydawnictwa Naukowo-Techniczne, Warszawa 1998

---