PEE Moduł 9: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd1.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd1.png|500px]] | ||
|valign="top"|'''Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów''' | |valign="top"|'''Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów''' | ||
|} | |} | ||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd2.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd2.png|500px]] | ||
|valign="top"|Weźmy pod uwagę obwód złożony z dowolnych elementów pasywnych RLCM i źródeł sterowanych nie zawierających wewnątrz żadnych źródeł niezależnych. Wyróżnijmy w tym obwodzie jedną parę zacisków uważanych za wejściowe, do których przykładamy źródło wymuszające oraz drugą parę zacisków wyjściowych, z których zbieramy prąd (zaciski zwarte) lub napięcie (zaciski rozwarte). | |valign="top"|Weźmy pod uwagę obwód złożony z dowolnych elementów pasywnych <math>RLCM</math> i źródeł sterowanych nie zawierających wewnątrz żadnych źródeł niezależnych. Wyróżnijmy w tym obwodzie jedną parę zacisków uważanych za wejściowe, do których przykładamy źródło wymuszające oraz drugą parę zacisków wyjściowych, z których zbieramy prąd (zaciski zwarte) lub napięcie (zaciski rozwarte). | ||
Transmitancja operatorowa określa związek między transformatą operatorową sygnału wyjściowego (odpowiedzi), którą tutaj oznaczymy w ogólności przez Y(s) oraz transformatą operatorową wymuszenia (sygnału wejściowego), oznaczoną ogólnie przez X(s). Transmitancją operatorową nazywać będziemy stosunek transformaty sygnału wyjściowego (prądu lub napięcia) do transformaty sygnału wejściowego układu (źródła napięciowego lub prądowego) przy zerowych warunkach początkowych | Transmitancja operatorowa określa związek między transformatą operatorową sygnału wyjściowego (odpowiedzi), którą tutaj oznaczymy w ogólności przez <math>Y(s)</math> oraz transformatą operatorową wymuszenia (sygnału wejściowego), oznaczoną ogólnie przez <math>X(s)</math>. Transmitancją operatorową nazywać będziemy stosunek transformaty sygnału wyjściowego (prądu lub napięcia) do transformaty sygnału wejściowego układu (źródła napięciowego lub prądowego) przy zerowych warunkach początkowych | ||
: <math>T(s)=\frac{Y(s)}{X(s)}</math> | : <math>T(s)=\frac{Y(s)}{X(s)}</math> | ||
| Linia 20: | Linia 20: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd3.png|500px]] | ||
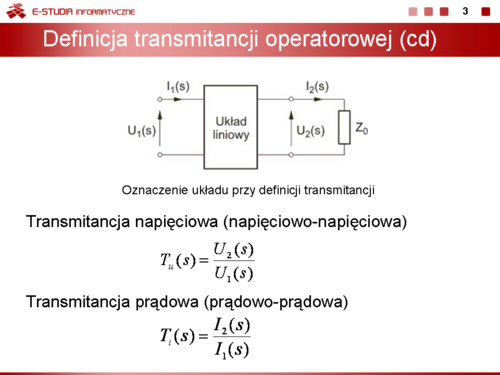
|valign="top"|Przyjmijmy oznaczenie bramy wejściowej cyfrą 1 a bramy wyjściowej cyfrą 2 jak to pokazano na slajdzie obok. | |valign="top"|Przyjmijmy oznaczenie bramy wejściowej cyfrą 1 a bramy wyjściowej cyfrą 2 jak to pokazano na slajdzie obok. | ||
| Linia 43: | Linia 43: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd4.png|500px]] | ||
|valign="top"|'''Transmitancja napięciowo-prądowa''' | |valign="top"|'''Transmitancja napięciowo-prądowa''' | ||
| Linia 69: | Linia 69: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd5.png|500px]] | ||
|valign="top"|Przy założeniu zerowych warunków początkowych dla indukcyjności i pojemności modele tych elementów nie zawierają źródeł a jedynie impedancje operatorowe <math>Z(s)</math>. Zestaw impedancji operatorowych dla elementów pasywnych przedstawiono na slajdzie 5. | |valign="top"|Przy założeniu zerowych warunków początkowych dla indukcyjności i pojemności modele tych elementów nie zawierają źródeł a jedynie impedancje operatorowe <math>Z(s)</math>. Zestaw impedancji operatorowych dla elementów pasywnych przedstawiono na slajdzie 5. | ||
| Linia 92: | Linia 92: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd6.png|500px]] | ||
|valign="top"|'''Odpowiedzią impulsową''' układu nazywamy jego odpowiedź czasową na wymuszenie w postaci impulsu Diraca przy zerowych warunkach początkowych obwodu. Dla wyznaczenia odpowiedzi impulsowej wykorzystuje się pojęcie transmitancji operatorowej <math>T(s)</math>. Transformata funkcji impulsowej Diraca jest równa <math>1</math>, zatem obliczając odpowiedź obwodu przyjmiemy wymuszenie <math>X(s)=1</math>. Bezpośrednio z definicji transmitancji wynika | |valign="top"|'''Odpowiedzią impulsową''' układu nazywamy jego odpowiedź czasową na wymuszenie w postaci impulsu Diraca przy zerowych warunkach początkowych obwodu. Dla wyznaczenia odpowiedzi impulsowej wykorzystuje się pojęcie transmitancji operatorowej <math>T(s)</math>. Transformata funkcji impulsowej Diraca jest równa <math>1</math>, zatem obliczając odpowiedź obwodu przyjmiemy wymuszenie <math>X(s)=1</math>. Bezpośrednio z definicji transmitancji wynika | ||
| Linia 118: | Linia 118: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd7.png|500px]] | ||
|valign="top"|Dla zilustrowania rozważań teoretycznych obliczmy odpowiedź impulsową i skokową układu o zadanej transmitancji operatorowej | |valign="top"|Dla zilustrowania rozważań teoretycznych obliczmy odpowiedź impulsową i skokową układu o zadanej transmitancji operatorowej | ||
| Linia 147: | Linia 147: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd8.png|500px]] | ||
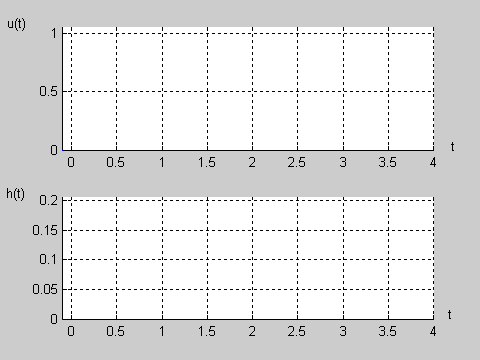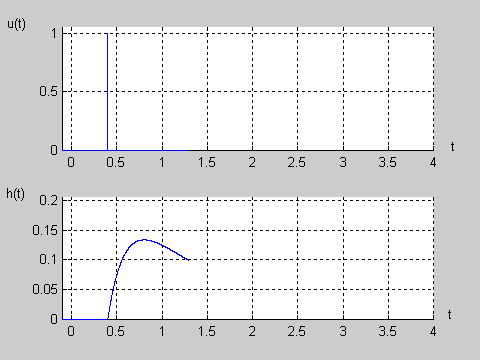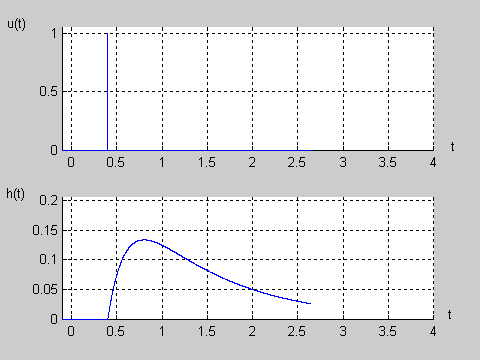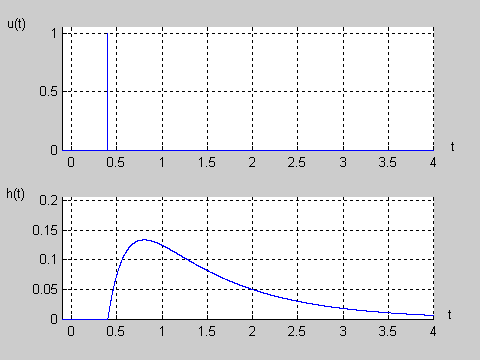
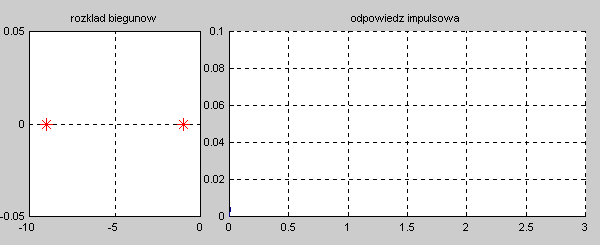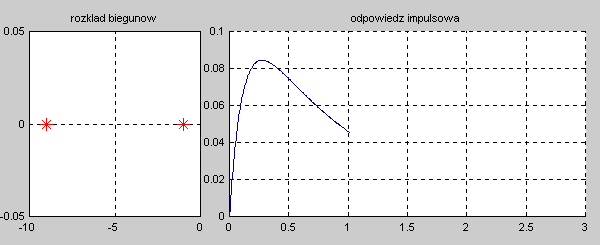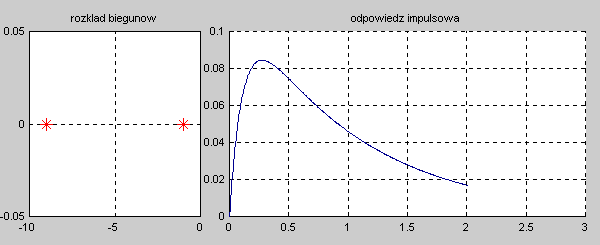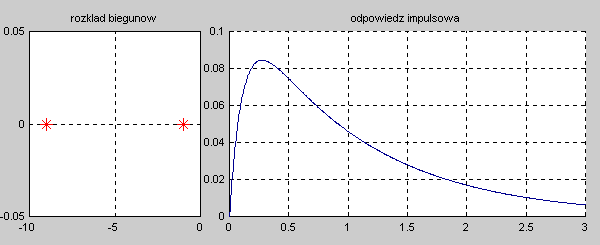
|valign="top"|Na slajdzie obok i animacjach poniżej przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej <math>T(s)</math>. | |valign="top"|Na slajdzie obok i animacjach poniżej przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej <math>T(s)</math>. | ||
| Linia 160: | Linia 160: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd9.png|500px]] | ||
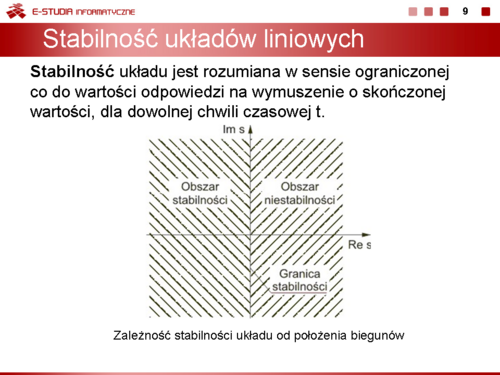
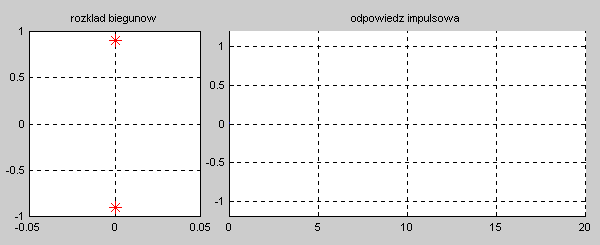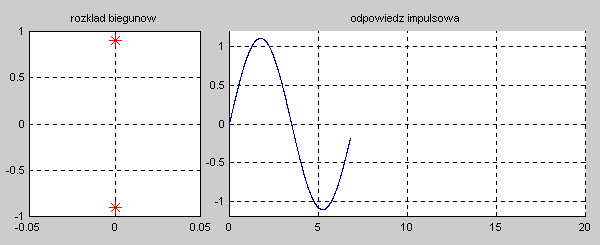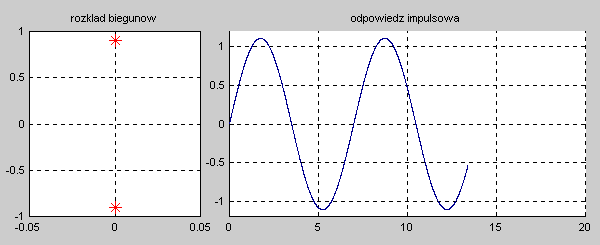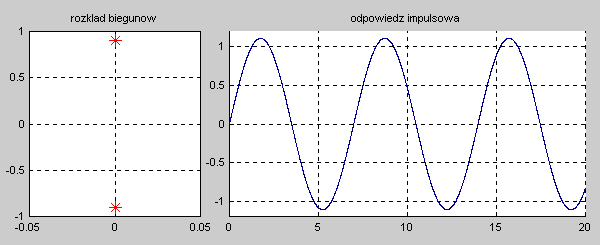
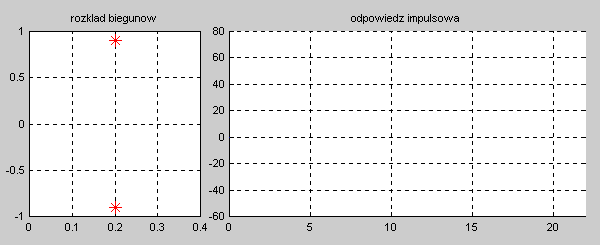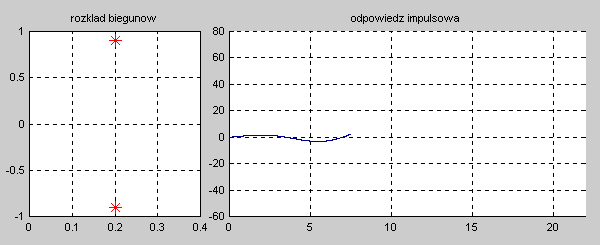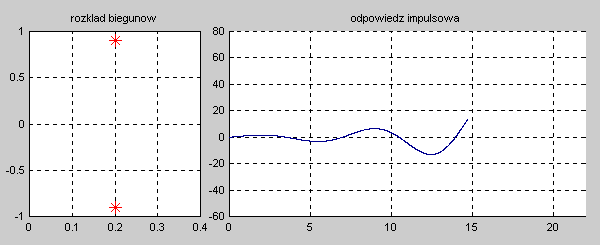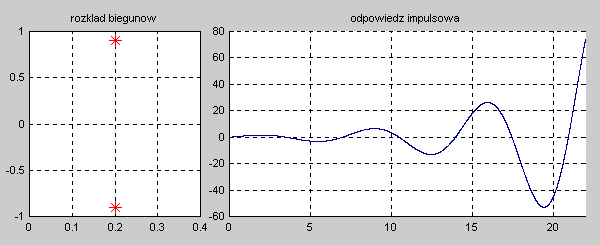
|valign="top"|'''Stabilność układu''' jest rozumiana w sensie ograniczonej co do wartości odpowiedzi na wymuszenie o skończonej wartości, dla dowolnej chwili czasowej <math>t</math>. Układ nazywać będziemy stabilnym, jeśli jego odpowiedź czasowa na skończoną wartość pobudzenia będzie ograniczona co do wartości w dowolnej chwili czasowej <math>t</math>. Stabilność wymaga, aby przy zaniku pobudzenia odpowiedź układu w stanie ustalonym przy <math>t \to \infty</math> była ograniczona co do wartości (stabilność w sensie zwykłym) lub zerowa (stabilność w sensie asymptotycznym). Oznacza to, że dla układów stabilnych odpowiedź w stanie przejściowym powinna zanikać do zera lub co najmniej nie narastać, pozostając na ustalonym poziomie. | |valign="top"|'''Stabilność układu''' jest rozumiana w sensie ograniczonej co do wartości odpowiedzi na wymuszenie o skończonej wartości, dla dowolnej chwili czasowej <math>t</math>. Układ nazywać będziemy stabilnym, jeśli jego odpowiedź czasowa na skończoną wartość pobudzenia będzie ograniczona co do wartości w dowolnej chwili czasowej <math>t</math>. Stabilność wymaga, aby przy zaniku pobudzenia odpowiedź układu w stanie ustalonym przy <math>t \to \infty</math> była ograniczona co do wartości (stabilność w sensie zwykłym) lub zerowa (stabilność w sensie asymptotycznym). Oznacza to, że dla układów stabilnych odpowiedź w stanie przejściowym powinna zanikać do zera lub co najmniej nie narastać, pozostając na ustalonym poziomie. | ||
| Linia 179: | Linia 179: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd10.png|500px]] | ||
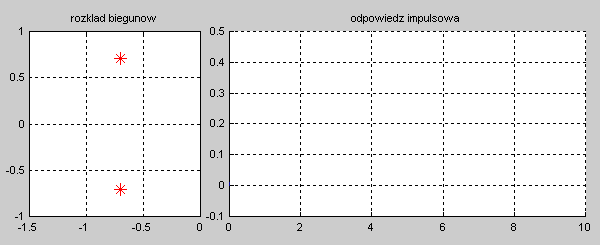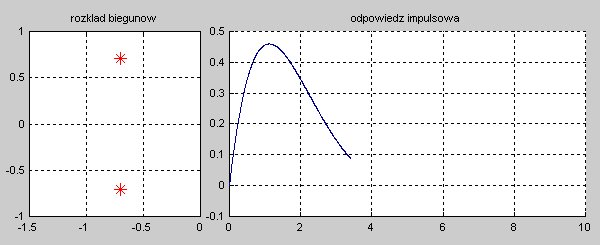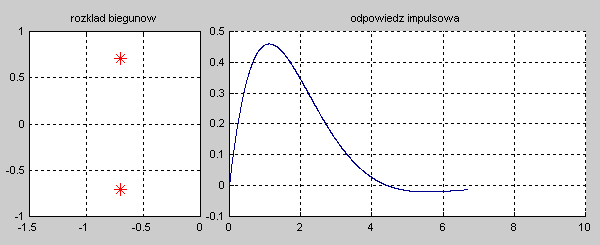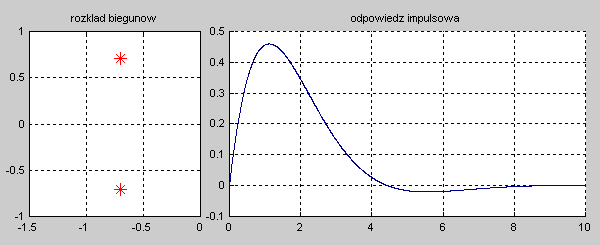
|valign="top"|Na slajdzie obok i poniższych animacjach zilustrowano wpływ położenia biegunów na stabilność układu. Oś urojona rozgraniczająca obszar stabilny od niestabilnego jest obszarem warunkowo stabilnym (stabilny w sensie zwykłym przy biegunach jednokrotnych i niestabilny przy biegunach wielokrotnych). | |valign="top"|Na slajdzie obok i poniższych animacjach zilustrowano wpływ położenia biegunów na stabilność układu. Oś urojona rozgraniczająca obszar stabilny od niestabilnego jest obszarem warunkowo stabilnym (stabilny w sensie zwykłym przy biegunach jednokrotnych i niestabilny przy biegunach wielokrotnych). | ||
| Linia 196: | Linia 196: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd11.png|500px]] | ||
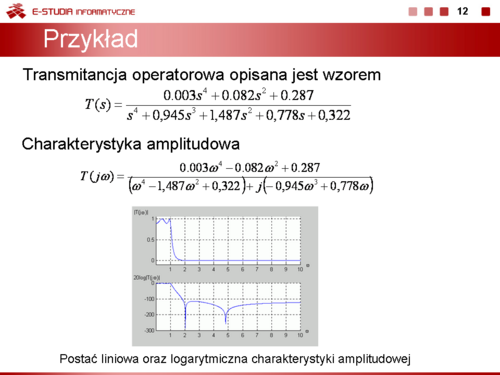
|valign="top"|'''Charakterystyką częstotliwościową''' układu nazywać będziemy zależność wartości sygnału wyjściowego tego układu od częstotliwości przy jednostkowym wymuszeniu sinusoidalnym przyłożonym na wejście układu. Charakterystykę tę można wyznaczyć bezpośrednio na podstawie transmitancji operatorowej T(s). Nosi ona nazwę '''transmitancji widmowej''' układu. | |valign="top"|'''Charakterystyką częstotliwościową''' układu nazywać będziemy zależność wartości sygnału wyjściowego tego układu od częstotliwości przy jednostkowym wymuszeniu sinusoidalnym przyłożonym na wejście układu. Charakterystykę tę można wyznaczyć bezpośrednio na podstawie transmitancji operatorowej T(s). Nosi ona nazwę '''transmitancji widmowej''' układu. | ||
| Linia 218: | Linia 218: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd12.png|500px]] | ||
|valign="top"|Jako przykład rozpatrzmy transmitancję operatorową opisaną wzorem | |valign="top"|Jako przykład rozpatrzmy transmitancję operatorową opisaną wzorem | ||
| Linia 243: | Linia 243: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd13.png|500px]] | ||
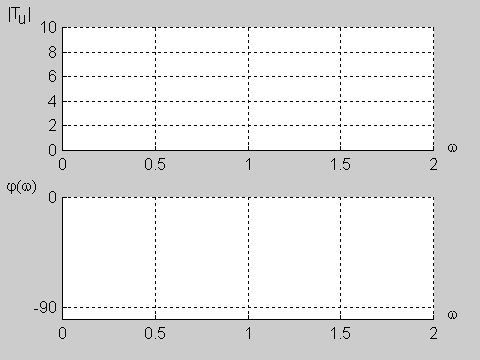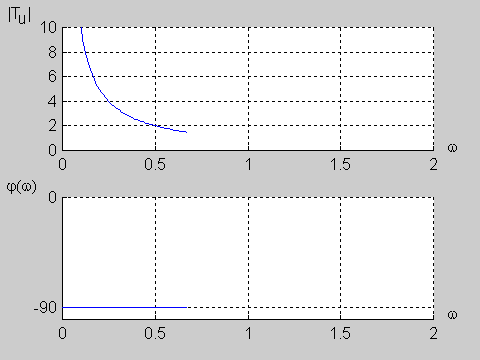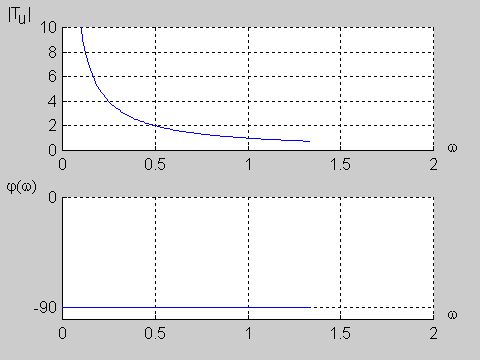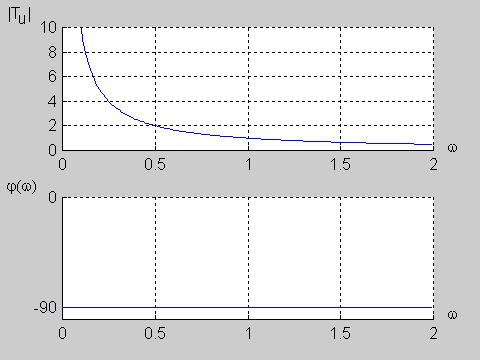
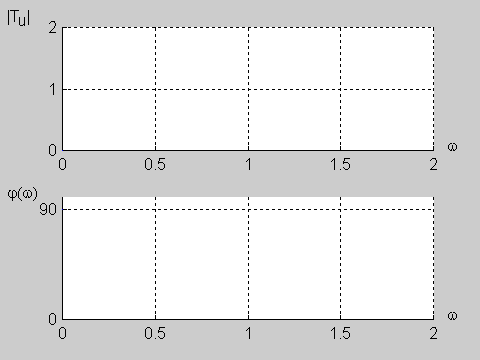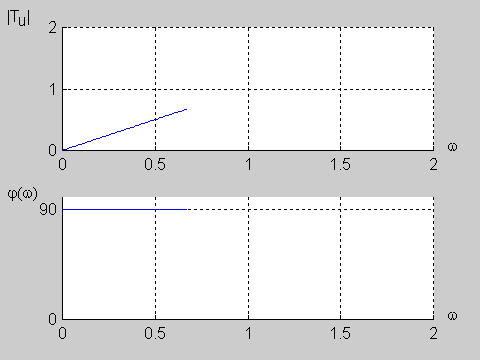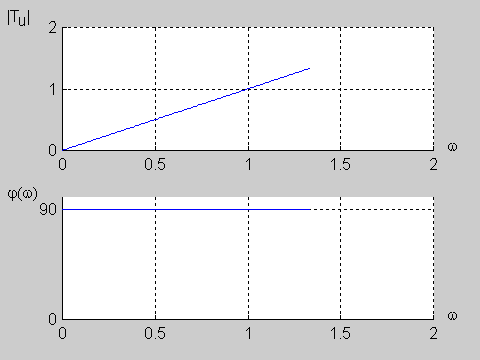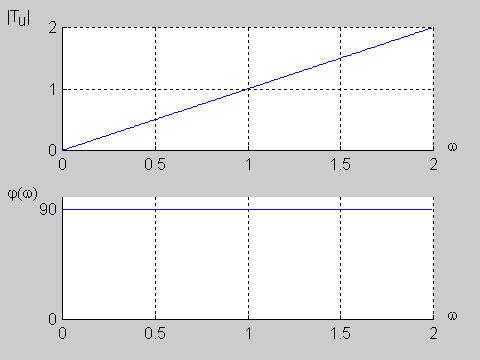
|valign="top"|W praktyce inżynierskiej zdefiniowano wiele użytecznych postaci transmitancji operatorowych. Tutaj ograniczymy się jedynie do trzech najprostszych transmitancji pierwszego rzędu: układu całkującego, różniczkującego oraz przesuwnika fazowego. | |valign="top"|W praktyce inżynierskiej zdefiniowano wiele użytecznych postaci transmitancji operatorowych. Tutaj ograniczymy się jedynie do trzech najprostszych transmitancji pierwszego rzędu: układu całkującego, różniczkującego oraz przesuwnika fazowego. | ||
| Linia 277: | Linia 277: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd14.png|500px]] | ||
|valign="top"|'''Układ różniczkujący''' | |valign="top"|'''Układ różniczkujący''' | ||
| Linia 305: | Linia 305: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd15.png|500px]] | ||
|valign="top"|'''Przesuwnik fazowy''' | |valign="top"|'''Przesuwnik fazowy''' | ||
| Linia 334: | Linia 334: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd16.png|500px]] | ||
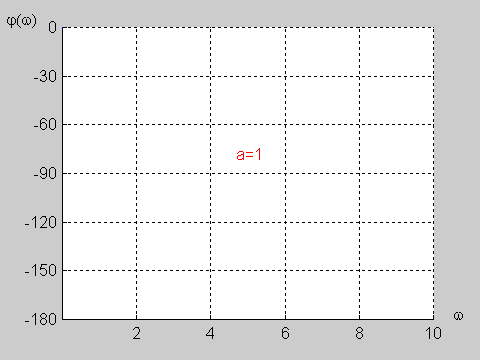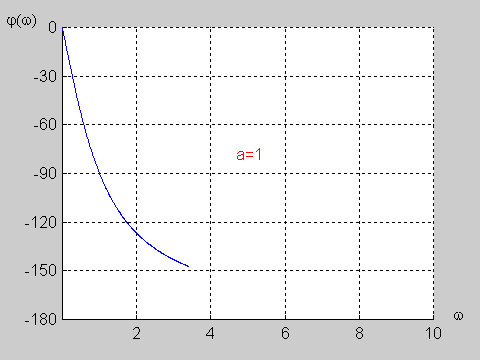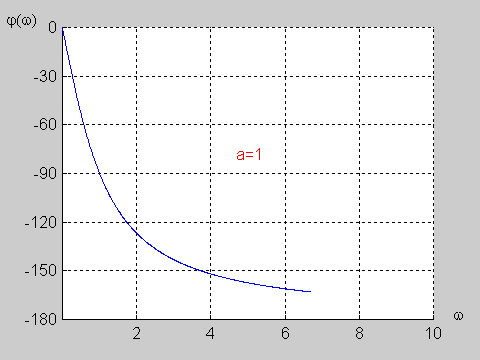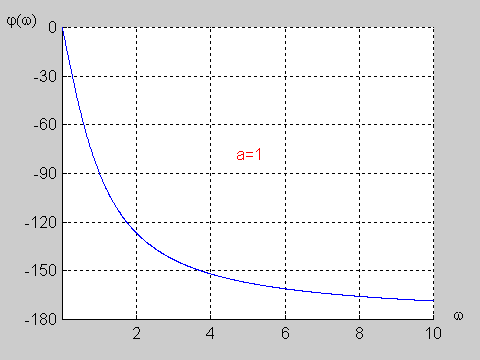
|valign="top"|Najbardziej ogólnym przypadkiem jest układ opisany transmitancją operatorową T(s) n-tego rzędu o postaci ogólnej zadanej wzorem | |valign="top"|Najbardziej ogólnym przypadkiem jest układ opisany transmitancją operatorową T(s) n-tego rzędu o postaci ogólnej zadanej wzorem | ||
| Linia 373: | Linia 373: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd17.png|500px]] | ||
|valign="top"|Jako przykład wyznaczymy transmitancję operatorową typu napięciowego obwodu (górny rysunek na slajdzie obok). Przyjmijmy: <math>R=1\Omega</math>, <math>L=2H\,</math>, <math>C=1F\,</math>. | |valign="top"|Jako przykład wyznaczymy transmitancję operatorową typu napięciowego obwodu (górny rysunek na slajdzie obok). Przyjmijmy: <math>R=1\Omega</math>, <math>L=2H\,</math>, <math>C=1F\,</math>. | ||
| Linia 383: | Linia 383: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M9_Slajd18.png]] | |valign="top" width="500px"|[[Grafika:PEE_M9_Slajd18.png|500px]] | ||
|valign="top"|Kolejne etapy wyznaczania transmitancji: | |valign="top"|Kolejne etapy wyznaczania transmitancji: | ||
| Linia 406: | Linia 406: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top"|'''Zadania sprawdzające''' | |valign="top"|'''Zadania sprawdzające''' | ||
| Linia 441: | Linia 440: | ||
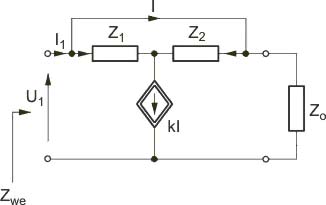
: <math>Z_{we}=\frac{U_1}{I_1}=\frac{Z_1+Z_2-Z_1k}{kZ_2Y_0+Y_0(Z_1+Z_2)}</math> | : <math>Z_{we}=\frac{U_1}{I_1}=\frac{Z_1+Z_2-Z_1k}{kZ_2Y_0+Y_0(Z_1+Z_2)}</math> | ||
---- | |||
''Zadanie 9.2'' | ''Zadanie 9.2'' | ||
Wersja z 12:32, 7 wrz 2006

|
Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów |
|
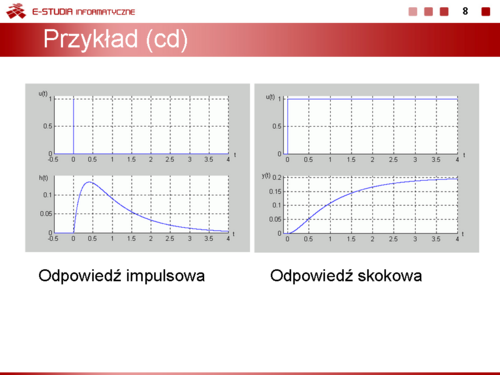
Na slajdzie obok i animacjach poniżej przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej . |

|
Najbardziej ogólnym przypadkiem jest układ opisany transmitancją operatorową T(s) n-tego rzędu o postaci ogólnej zadanej wzorem
Załączony do podręcznika program interakcyjny CHARAKTERYSTYKI umożliwia wykreślanie charakterystyk częstotliwościowych (amplitudowych i fazowych) układów opisanych za pomocą transmitancji operatorowej o postaci określonej wzorem powyższym. Transmitancja widmowa takiego układu wyznaczana jest z transmitancji operatorowej przez podstawienie . W wyniku otrzymuje się Transmitancja widmowa przedstawia sobą funkcję zespoloną pulsacji i może być zapisana w postaci ogólnej jako Część rzeczywista i urojona są funkcjami zarówno współczynników , licznika i mianownika transmitancji operatorowej, jak i aktualnej wartości pulsacji . Charakterystyka amplitudowa przedstawia sobą moduł transmitancji widmowej określony wzorem Charakterystyka fazowa jest fazą transmitancji widmowej i wyznaczana jest z zależności |
| <applet code="filtr.class" archive="images/6/6a/PEE_M9_filtr.jar" width="462" height="363">
</applet> |
Omawiane zależności zostały wykorzystane do badania charakterystyk częstotliwościowych układów opisanych transmitancją operatorową zadawaną przez użytkownika.
Użytkownik ustala stopień licznika i mianownika transmitancji, a także wartości wszystkich współczynników wielomianu licznika i mianownika. Określa również zakres pulsacji, dla którego wykreślane będą charakterystyki częstotliwościowe. W programie założono, że maksymalny rząd układu nie powinien przekroczyć wartości 9. Wykorzystując podane wcześniej zależności częstotliwościowe program wykreśla charakterystyki amplitudowe (liniową i logarytmiczną wyrażoną w decybelach) oraz charakterystykę fazową w stopniach. Charakterystyki filtru zostają wykreślone w oddzielnych oknach, pozwalających na skalowanie oraz oglądanie w powiększeniu poszczególnych odcinków krzywych. |
|
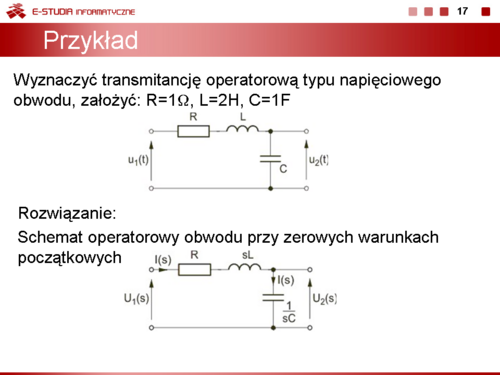
Jako przykład wyznaczymy transmitancję operatorową typu napięciowego obwodu (górny rysunek na slajdzie obok). Przyjmijmy: , , .
|

|
Kolejne etapy wyznaczania transmitancji:
Prąd I(s) Napięcie wyjściowe Transmitancja napięciowa Po podstawieniu wartości liczbowych otrzymuje się |
| Zadania sprawdzające
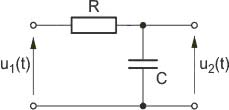
Wyznaczyć impedancję wejściową w postaci operatorowej dla obwodu przedstawionego na poniższym rysunku. Impedancję wejściową potraktować jako transmitancję napięciowo-prądową.
Rozwiązanie Z prawa prądowego i napięciowego Kirchhoffa napisanych dla obwodu z powyzszego rysunku otrzymuje się
Zadanie 9.2 Wyznaczyć charakterystyki częstotliwościowe obwodu przedstawionego na poniższym rysunku biorąc pod uwagę transmitancję napięciową.
Transmitancja napięciowa obwodu określona jest wzorem
|