PEE Moduł 3: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd1.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd1.png|500px]] | ||
|valign="top"|'''Wykład 3. Zagadnienia mocy w obwodach RLC przy wymuszeniu sinusoidalnym''' | |valign="top"|'''Wykład 3. Zagadnienia mocy w obwodach RLC przy wymuszeniu sinusoidalnym''' | ||
|} | |} | ||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd2.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd2.png|500px]] | ||
|valign="top"|'''Moc chwilowa ''' | |valign="top"|'''Moc chwilowa ''' | ||
| Linia 24: | Linia 24: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd3.png|500px]] | ||
|valign="top"|'''Moc czynna''' | |valign="top"|'''Moc czynna''' | ||
| Linia 40: | Linia 40: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd4.png|500px]] | ||
|valign="top"|Moc czynna stanowi składową stałą mocy chwilowej. Jest ona nieujemna dla obwodu RLC a w granicznym przypadku przy <math>\varphi=\pm\pi/2\rightarrow P_L=P_C=0 </math> jest równa zeru. Moc czynna osiąga wartość największą <math>P=|U||I|</math> wtedy, gdy <math>\varphi=0</math> to znaczy gdy odbiornik ma charakter rezystancyjny, <math>cos\varphi=1</math> Wartość najmniejszą <math>(P=0)</math> moc osiąga w przypadku granicznym, gdy <math>\varphi=\pm\pi/2</math> to znaczy gdy odbiornikiem jest cewka idealna lub kondensator idealny, <math>cos\varphi=0</math> Oznacza to, że '''na elementach reaktancyjnych nie wydziela się moc czynna'''. | |valign="top"|Moc czynna stanowi składową stałą mocy chwilowej. Jest ona nieujemna dla obwodu RLC a w granicznym przypadku przy <math>\varphi=\pm\pi/2\rightarrow P_L=P_C=0 </math> jest równa zeru. Moc czynna osiąga wartość największą <math>P=|U||I|</math> wtedy, gdy <math>\varphi=0</math> to znaczy gdy odbiornik ma charakter rezystancyjny, <math>cos\varphi=1</math> Wartość najmniejszą <math>(P=0)</math> moc osiąga w przypadku granicznym, gdy <math>\varphi=\pm\pi/2</math> to znaczy gdy odbiornikiem jest cewka idealna lub kondensator idealny, <math>cos\varphi=0</math> Oznacza to, że '''na elementach reaktancyjnych nie wydziela się moc czynna'''. | ||
| Linia 55: | Linia 55: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd5.png|500px]] | ||
|valign="top"|'''Moc bierna''' | |valign="top"|'''Moc bierna''' | ||
| Linia 73: | Linia 73: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd6.png|500px]] | ||
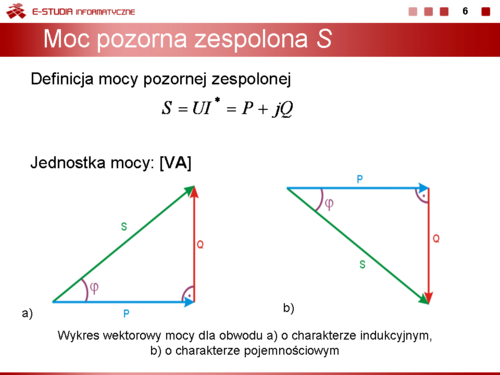
|valign="top"|'''Moc pozorna zespolona''' | |valign="top"|'''Moc pozorna zespolona''' | ||
| Linia 82: | Linia 82: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd7.png|500px]] | ||
|valign="top"|Zależność na moc pozorną zespoloną można przedstawić również w postaci wykładniczej <math>S=|S|e^j^\varphi</math> W zależności tej <math>|S|</math> wyraża '''moduł mocy pozornej zespolonej''', który może być wyrażony w postaci iloczynu modułów wartości skutecznych prądu i napięcia | |valign="top"|Zależność na moc pozorną zespoloną można przedstawić również w postaci wykładniczej <math>S=|S|e^j^\varphi</math> W zależności tej <math>|S|</math> wyraża '''moduł mocy pozornej zespolonej''', który może być wyrażony w postaci iloczynu modułów wartości skutecznych prądu i napięcia | ||
| Linia 97: | Linia 97: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd7.png|500px]] | ||
|valign="top"| | |valign="top"| | ||
Dla ułatwienia korzystania z pojęć mocy zestawiono poniżej najważniejsze postacie wzorów na moc czynną, bierną i pozorną | Dla ułatwienia korzystania z pojęć mocy zestawiono poniżej najważniejsze postacie wzorów na moc czynną, bierną i pozorną | ||
| Linia 119: | Linia 119: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd8.png|500px]] | ||
|valign="top"|'''Bilans mocy''' | |valign="top"|'''Bilans mocy''' | ||
| Linia 138: | Linia 138: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd10.png|500px]] | ||
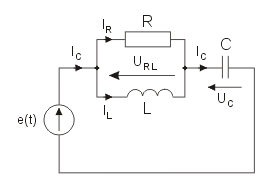
|valign="top"|Dla zilustrowania wprowadzonych tu pojęć mocy oraz zasady bilansowania się mocy rozpatrzymy przykład obwodu przedstawionego na rysunku. | |valign="top"|Dla zilustrowania wprowadzonych tu pojęć mocy oraz zasady bilansowania się mocy rozpatrzymy przykład obwodu przedstawionego na rysunku. | ||
| Linia 153: | Linia 153: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd11.png|500px]] | ||
|valign="top"|''Rozwiązanie'' | |valign="top"|''Rozwiązanie'' | ||
| Linia 172: | Linia 172: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd12.png|500px]] | ||
|valign="top"|Napięcia na poszczególnych elementach obwodu dane są w postaci | |valign="top"|Napięcia na poszczególnych elementach obwodu dane są w postaci | ||
| Linia 192: | Linia 192: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd13.png|500px]] | ||
|valign="top"| | |valign="top"| | ||
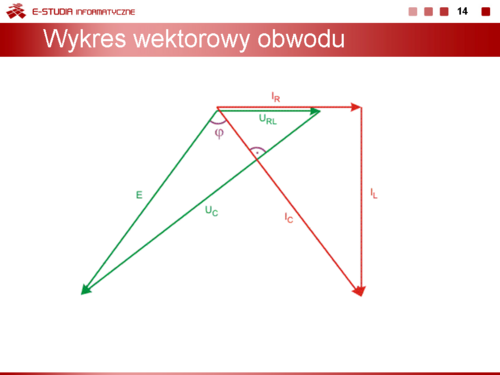
Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie. | Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie. | ||
| Linia 204: | Linia 204: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd14.png|500px]] | ||
|valign="top"|Poszczególne rodzaje mocy wydzielonej w obwodzie równają się: | |valign="top"|Poszczególne rodzaje mocy wydzielonej w obwodzie równają się: | ||
| Linia 232: | Linia 232: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd15.png|500px]] | ||
|valign="top"|'''Energia magazynowana w idealnym kondensatorze''' | |valign="top"|'''Energia magazynowana w idealnym kondensatorze''' | ||
| Linia 258: | Linia 258: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd16.png|500px]] | ||
|valign="top"|'''Energia magazynowana w idealnej cewce''' | |valign="top"|'''Energia magazynowana w idealnej cewce''' | ||
Wersja z 08:51, 6 wrz 2006

|
Wykład 3. Zagadnienia mocy w obwodach RLC przy wymuszeniu sinusoidalnym |
| <applet code="moce_demo.class" archive="images/a/a9/PEE_M3_moce.jar" width="600" height="580"></applet> | Umieszczony obok program pozwala na analizę w trybie on-line obwodu RLC o strukturze przedstawionej na rysunku. Użytkownik wybiera elementy obwodu włączone w strukturę i wpisuje ich wartości. Po naciśnięciu przycisku OBLICZ program automatycznie obliczy wartości wszystkich prądów, napięć i mocy elementów, podając jednocześnie bilans mocy. |

|
Rozwiązanie
Wartości zespolone impedancji i napięcia wymuszającego w obwodzie przy danych wartościach elementów są równe: Impedancja zastępcza połączenia równoległego L i R równa się Impedancja zastępcza połączenia szeregowego i jest równa |

|
Napięcia na poszczególnych elementach obwodu dane są w postaci
|
|
Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie.
|

|
Poszczególne rodzaje mocy wydzielonej w obwodzie równają się:
Moc wydzielona na rezystorze oraz cewce i kondensatorze równa się dokładnie mocy dostarczonej przez źródło. Bilans mocy generowanej przez źródło i mocy wydzielonej w odbiorniku jest zatem równy zeru. |

|
Energia magazynowana w idealnym kondensatorze
Cewka i kondensator traktowane jako idealne elementy obwodowe należą do elementów magazynujących energię elektryczną. Rozpatrzmy kondensator o pojemności zasilony z generatora napięciowego . Obliczymy energię dostarczoną do tego kondensatora w czasie od do . Energia ta może być obliczona jako całka z mocy chwilowej Uwzględniając wzór na moc chwilową i dokonując odpowiednich operacji całkowania otrzymujemy Uwzględniając wzór na moc chwilową i dokonując odpowiednich operacji całkowania otrzymujemy Zasadniczą cechą kondensatora idealnego jest jego bezstratność, co oznacza, że energia zgromadzona na nim pozostaje w nim zmagazynowana. Zatem kondensator naładowany do napięcia stałego U posiada energię równą Jest to bardzo ważna własność kondensatora, wykorzystywana do magazynowania energii elektrycznej. |

|
Energia magazynowana w idealnej cewce
Rozpatrzmy cewkę o indukcyjności zasiloną z generatora napięciowego . Obliczymy energię dostarczoną do tej cewki w czasie od do . Energia ta, podobnie jak w przypadku kondensatora, może być obliczona jako całka z mocy chwilowej Uwzględniając wzór na moc chwilową i dokonując odpowiednich operacji całkowania otrzymujemy Załóżmy, że czas t0 jest taką chwilą, w której prąd cewki jest zerowy. W takim razie wzór na energię upraszcza się do postaci Zasadniczą cechą cewki idealnej jest jej bezstratność, co oznacza, że energia dostarczona do niej pozostaje w niej zmagazynowana. Zatem cewka, przez która przepływa prąd stały I posiada energię równą W odróżnieniu od kondensatora, w którym energia związana była z napięciem między okładkami (ładunkiem) energia cewki jest uzależniona od prądu (strumienia magnetycznego). Stąd przyjmuje się, że kondensator magazynuje energię w polu elektrycznym a cewka w polu magnetycznym. |
| Zadania sprawdzające
Zadanie 3.1 Sporządzić bilans mocy w obwodzie przedstawionym na rysunku. Przyjąć następujące wartości elementów: .
Wartości symboliczne elementów obwodu:
|