PS Moduł 6

W zastosowaniach teorii sygnałów często porównujemy analizowanego sygnału z innym sygnałem, w szczególności ¬z swoją własną przesuniętą w czasie kopią. Podobieństwo sygnałów można charakteryzować za pomocą funkcji korelacyjnych. Przypomnijmy, że na podstawie iloczynu skalarnego możemy wyznaczyć zarówno odległość dwóch sygnałów, jak i kąt między nimi w danej przestrzeni Hilberta. Jeśli $x(t)\in L^2$ , to także $x_{\tau }(t)\in L^2$. Dla różnych wartości przesunięcia $\tau$ całka definicyjna (6.1) przybiera różne wartości. W ten sposób otrzymujemy zależność funkcyjną od zmiennej $\tau$ . Dla ustalonego $\tau$ wartość funkcji autokorelacji jest polem pod wykresem iloczynu sygnału nieprzesuniętego i przesuniętego. Definicja (6.1) została podana od razu dla sygnałów zespolonych. Przedrostek „auto” oznacza, że funkcja korelacyjna (6.1) opisuje korelację czasową między danym sygnałem a wersją przesuniętą tego samego sygnału. Podkreślamy to dodając do symbolu Parser nie mógł rozpoznać (błąd składni): {\displaystyle "\varphi"\,} funkcji autokorelacji indeks sygnału Parser nie mógł rozpoznać (błąd składni): {\displaystyle "x"\,} .

---

Parzystość funkcji autokorelacji w przypadku sygnałów rzeczywistych oznacza, że możemy ją wówczas wyznaczać jedynie dla dodatnich wartości zmiennej $\tau$ (opóźnień sygnału). Wzór (6.2) wynika z podstawienia $\tau =0$ we wzorze definiującym funkcję autokorelacji. Funkcja autokorelacji przybiera maksymalną co do modułu wartość dla $\tau =0$ . Brak korelacji czasowej sygnałów oznacza ich ortogonalność. Funkcja autokorelacji sygnału $x(t)\in L^2$ jest $F$ - transformowalna w zwykłym sensie. Funkcja autokorelacji jest niezmiennicza względem przesunięcia, tj. ${\phi }_x(\tau )={\phi }_{x_{t_0}}(\tau )$ dla dowolnego $t_0$ , gdzie $x_{t_0}(t)=x(t-t_0)$.

---

Przedstawione na rysunku funkcje autokorelacji można wyznaczyć wprost z definicji. Wszystkie funkcje mają jedyne maksimum w punkcie $\tau =0$. Funkcja autokorelacji impulsu prostokątnego jest trójkątna. Sposób jej konstrukcji jest pokazany na rys. e. Trójkątny kształt funkcji autokorelacji występuje również w przypadku ciągu impulsów prostokątnych i prostokątnego impulsu radiowego.

---

Słuszność pary transformat (6.3) można wykazać na podstawie twierdzenia Rayleigha dla klasy sygnałów $L^2$ i twierdzenia o przesunięciu. Ponieważ $F[x(t-\tau )]=X(\omega )e^{-j\omega \tau }$ , zatem: $\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(t)x^{*}(t-\tau )d\tau =\frac{1}{2\pi }\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}X(\omega )X^{*}(\omega )e^{j\omega \tau }d\omega =\frac{1}{2\pi }\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}|X(\omega ){|}^2{e}^{j\omega \tau }d\omega$ Energię sygnału można obliczyć: w dziedzinie czasu, jako całkę z kwadratu modułu sygnału, w dziedzinie korelacyjnej, jako ${\phi }_x(0)$, w dziedzinie częstotliwości, jako całkę z widma energii podzieloną przez $2\pi$.

---

Widmo energii jest zawsze funkcją rzeczywistą parzystą i opisuje rozkład energii wzdłuż osi częstotliwości. Energię sygnału zawartą w przedziale pulsacji $[{\omega }_1,omeg{a}_2]$ można wyznaczyć, obliczając całkę $E_x({\omega }_1,{\omega }_2)=\frac{1}{\pi }\underset{{\omega }_1}{\overset{{\omega }_2}{\int }}{\mathrm{\Phi }}_x(\omega )d\omega$ (por. rys. a). Funkcja autokorelacji idealnego sygnału dolnopasmowego $x(t)=X_{0}Sa{\omega }_{0}t$ ma również kształt funkcji $Sa$. Wynika to z faktu, że zarówno widmo amplitudowe tego sygnału, jak i jego widmo energii są prostokątne.

---

Związki między sygnałem i jego charakterystykami w dziedzinie częstotliwości i dziedzinie korelacyjnej ilustruje prosty diagram. Strzałki podwójne oznaczają na nim związki wzajemnie jednoznaczne, tj. jednoznaczne przejścia od jednej do drugiej wielkości , natomiast strzałki pojedyncze oznaczają przejście tylko w jedną stronę. Funkcja autokorelacji sygnału stanowi jedynie częściowy opis sygnału. Znając te funkcję możemy odtworzyć widmo amplitudowe sygnału, tracimy jednak informację o widmie fazowym. Podana definicja efektywnego czasu korelacji ma sens dla przypadku sygnałów, których funkcja autokorelacji maleje monotonicznie. Dla sygnałów o funkcji autokorelacji dążącej do zera oscylacyjnie można wprowadzić inne miary czasu korelacji. Zasada nieoznaczoności pozostaje w mocy bez względu na sposób definiowania efektywnego czasu korelacji i efektywnej szerokości widma.

---

Funkcje korelacji wzajemnej są określone dla dwóch różnych sygnałów (np. dla sygnału na wejściu i na wyjściu pewnego układu). Tak jak w przypadku funkcji autokorelacji, funkcje korelacji wzajemnej można traktować jako miary wzajemnego położenia sygnałów w odpowiedniej przestrzeni Hilberta dla różnych wartości przesunięcia jednego sygnału względem drugiego. Pojęcie energii wzajemnej ma interesującą interpretację fizyczną. Jeśli $x(t)$ i $y(t)$ są sygnałami napięcia i odpowiednio prądu na zaciskach dwójnika elektrycznego, to wielkość ${\phi }_{xy}=E_{xy}$ jest energią pobraną przez ten dwójnik. Dla ustalonego $\tau$ wartość funkcji korelacji wzajemnej jest polem pod wykresem iloczynu sygnałów (por. rys. c i d). W przeciwieństwie do funkcji autokorelacji, funkcje korelacji wzajemnej sygnałów rzeczywistych nie muszą być parzyste (por. rys. e).

---

Dla sygnałów rzeczywistych związek (6.4) przybiera postać ${\phi }_{xy}(\tau )={\phi }_{yx}(-\tau )$ , co oznacza, że taką samą wartość iloczynu skalarnego otrzymujemy przy przesunięciu sygnału $y(t)$ w kierunku opóźnienia o czas $\tau$ , co przy przesunięciu sygnału $x(t)$ o ten sam czas w kierunku przyspieszenia. Funkcje korelacji wzajemnej sygnałów o ograniczonej energii są $F$ -transformowalne w zwykłym sensie. Funkcje korelacji wzajemnej i widma energii wzajemnej tworzą pary transformat Fouriera.

---

Dla sygnałów o ograniczonej mocy funkcje korelacyjne definiujemy jako wielkości graniczne (dla odróżnienia oznaczamy je literą psi) . Właściwości funkcji autokorelacji sygnałów o ograniczonej mocy są podobne jak w przypadku sygnałów o ograniczonej energii. Wartość funkcji autokorelacji ${\psi }_x(\tau )$ sygnału o ograniczonej mocy w punkcie $\tau =0$ jest rzeczywista i równa jego mocy. Funkcja autokorelacji ${\psi }_x(\tau )$ przybiera maksymalną co do modułu wartość dla $\tau =0$. Brak korelacji czasowej sygnałów oznacza ich ortogonalność. Funkcja autokorelacji sygnału o ograniczonej mocy jest $F$ -transformowalna w sensie granicznym. Funkcja autokorelacji ${\psi }_x(\tau )$ jest niezmiennicza względem przesunięcia, tj. ${\psi }_x(\tau )={\psi }_{x_{t_0}}(\tau )$ dla dowolnego $t_0$ .

---

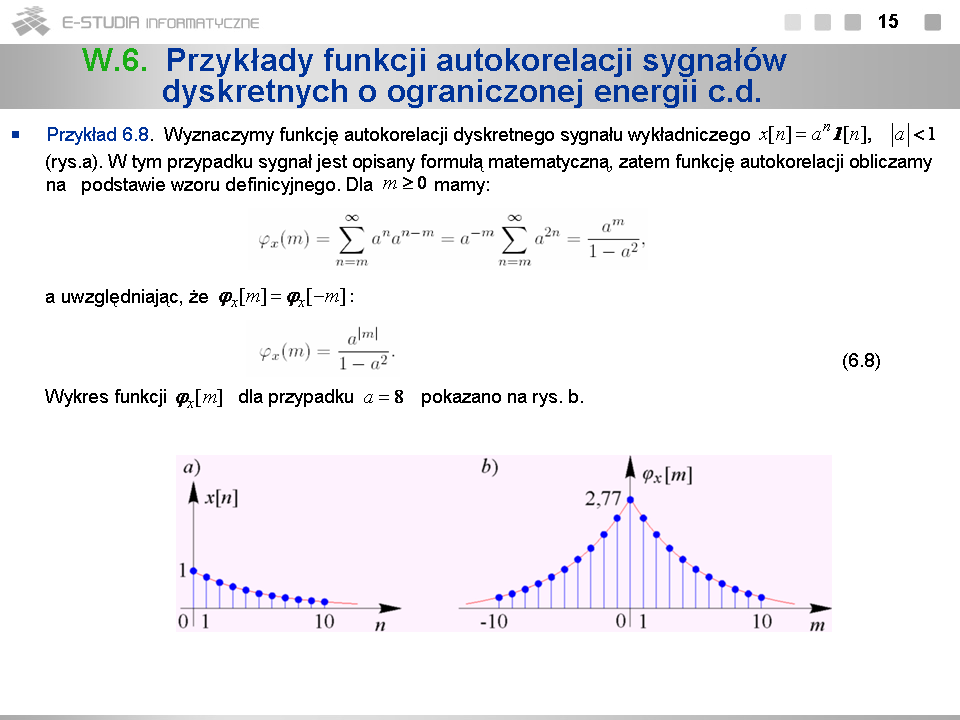
Funkcja autokorelacji skoku jednostkowego $1(t)$ jest stała i równa $1/2$ . Jeśli współczynnik wypełnienia $T/T_0$ unipolarnej fali prostokątnej jest mniejszy bądź równy $1/2$ , jej funkcja autokorelacji jest ciągiem trójkątów o szerokości $2T$ powtarzanych z okresowym $T_0$ (rys a). Jeśli $T/T_0>1/2$ , trójkąty te nakładają się na siebie i funkcja autokorelacji ma postać jak na rys b. Funkcja autokorelacji sygnału harmonicznego jest funkcją kosinusoidalną o tym samym okresie co okres sygnału harmonicznego i nie zależy od jego fazy początkowej ${\phi }_0$. Przykład ten świadczy dobitnie o tym, że funkcja autokorelacji nie zawiera informacji o fazie sygnału.

---

Definicja widma mocy ${\mathrm{\Psi }}_x(\omega )$ sygnału $x(t)$ o ograniczonej mocy ma sens graniczny. Widmo to jest określone jako granica ciągu widm energii ${\mathrm{\Phi }}_T(\omega )$ sygnałów impulsowych $x_T(t)$ będących centralnymi segmentami sygnału $x(t)$ o długości $T$ przy $T\to \mathrm{\infty }$ . Funkcja autokorelacji ${\psi }_x(\omega )$ i widmo mocy ${\mathrm{\Psi }}_x(\omega )$ sygnału $x(t)$ o ograniczonej mocy tworzą parę transformat Fouriera w sensie granicznym. Moc sygnału można obliczyć w dziedzinie częstotliwości jako całkę z widma mocy podzieloną przez $2\pi$. Widmo mocy opisuje zatem rozkład mocy sygnału wzdłuż osi pulsacji (częstotliwości). W przypadku sygnałów okresowych $x(t)$ funkcja autokorelacji ${\psi }_x(\omega )$ jest również okresowa, a więc rozwijalna w zespolony szereg Fouriera. Współczynnikami tego szeregu są kwadraty modułów $|X_k{|}^2$ współczynników $X_k$ zespolonego szeregu Fouriera sygnału $x(t)$ . Widmo mocy sygnału okresowego jest zatem dystrybucyjne.

---

---

---

---

---

---

---

---

---