PS Moduł 6: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 40: | Linia 40: | ||
|valign="top"| | |valign="top"| | ||
*Słuszność pary transformat (6.3) można wykazać na podstawie twierdzenia Rayleigha dla klasy sygnałów <math>L^2\,</math> i twierdzenia o przesunięciu. Ponieważ <math>F\, [x(t-\tau)]=X(\omega)e^{-j\omega \tau}</math> , zatem: | *Słuszność pary transformat (6.3) można wykazać na podstawie twierdzenia Rayleigha dla klasy sygnałów <math>L^2\,</math> i twierdzenia o przesunięciu. Ponieważ <math>F\, [x(t-\tau)]=X(\omega)e^{-j\omega \tau}</math> , zatem: | ||
<math>\int_{-\infty}^{\infty} x(t)x^{*}(t-\tau)\, d\tau=\frac{1}{2\pi}\int_{-\infty}^{\infty} X(\omega)X^{*}(\omega)e^{j\omega \tau}\, d\omega=\frac{1}{2\pi}\int_{-\infty}^{\infty} |X(\omega)|^2e^{j\omega \tau}\, d\omega</math> | <math>\int_{-\infty}^{\infty} x(t)x^{*}(t-\tau)\, d\tau=\frac{1}{2\pi}\int_{-\infty}^{\infty} X(\omega)X^{*}(\omega)e^{j\omega \tau}\, d\omega=\frac{1}{2\pi}\int_{-\infty}^{\infty} |X(\omega)|^2e^{j\omega \tau}\, d\omega</math> | ||
*Energię sygnału można obliczyć: | *Energię sygnału można obliczyć: | ||
| Linia 57: | Linia 55: | ||
|valign="top"| | |valign="top"| | ||
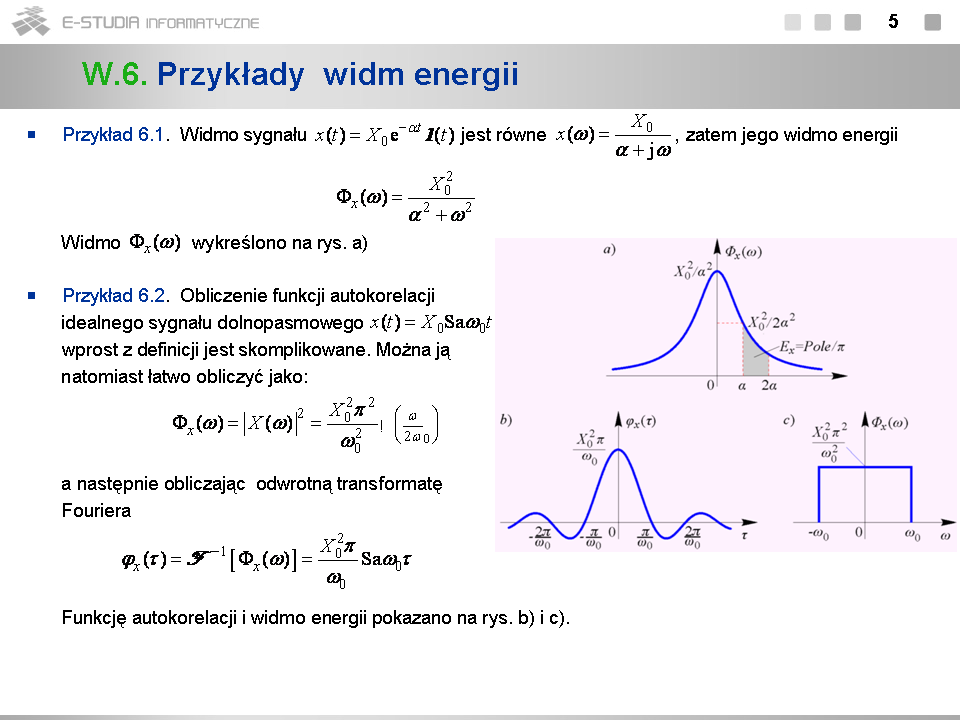
*Widmo energii jest zawsze funkcją rzeczywistą parzystą i opisuje rozkład energii wzdłuż osi częstotliwości. Energię sygnału zawartą w przedziale pulsacji <math>[\omega_1, omega_2]\,</math> można wyznaczyć, obliczając całkę | *Widmo energii jest zawsze funkcją rzeczywistą parzystą i opisuje rozkład energii wzdłuż osi częstotliwości. Energię sygnału zawartą w przedziale pulsacji <math>[\omega_1, omega_2]\,</math> można wyznaczyć, obliczając całkę | ||
<math>E_x(\omega_1, \omega_2)=\frac{1}{\pi}\int_{\omega_1}^{\omega_2} \Phi_x(\omega)\, d\omega</math> (por. rys. a). | <math>E_x(\omega_1, \omega_2)=\frac{1}{\pi}\int_{\omega_1}^{\omega_2} \Phi_x(\omega)\, d\omega</math> (por. rys. a). | ||
| Linia 81: | Linia 78: | ||
|width="500px" valign="top"|[[Grafika:PS_M6_Slajd7.png]] | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd7.png]] | ||
|valign="top"| | |valign="top"| | ||
*''Funkcje korelacji wzajemnej'' są określone dla dwóch różnych sygnałów (np. dla sygnału na wejściu i na wyjściu pewnego układu). Tak jak w przypadku funkcji autokorelacji, funkcje korelacji wzajemnej można traktować jako miary wzajemnego położenia sygnałów w odpowiedniej przestrzeni Hilberta dla różnych wartości przesunięcia jednego sygnału względem drugiego. | |||
*Pojęcie energii wzajemnej ma interesującą interpretację fizyczną. Jeśli <math>x(t)\,</math> i <math>y(t)\,</math> są sygnałami napięcia i odpowiednio prądu na zaciskach dwójnika elektrycznego, to wielkość <math>\varphi_{xy}=E_{xy}</math> jest energią pobraną przez ten dwójnik. | |||
*Dla ustalonego <math>\tau\,</math> wartość funkcji korelacji wzajemnej jest polem pod wykresem iloczynu sygnałów (por. rys. c i d). | |||
*W przeciwieństwie do funkcji autokorelacji, funkcje korelacji wzajemnej sygnałów rzeczywistych nie muszą być parzyste (por. rys. e). | |||
|} | |} | ||
| Linia 88: | Linia 89: | ||
|width="500px" valign="top"|[[Grafika:PS_M6_Slajd8.png]] | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd8.png]] | ||
|valign="top"| | |valign="top"| | ||
*Dla sygnałów rzeczywistych związek (6.4) przybiera postać <math>\varphi_{xy}(\tau)=\varphi_{yx}(-\tau)</math> , co oznacza, że taką samą wartość iloczynu skalarnego otrzymujemy przy przesunięciu sygnału <math>y(t)\,</math> w kierunku opóźnienia o czas <math>\tau\,</math> , co przy przesunięciu sygnału <math>x(t)\,</math> o ten sam czas w kierunku przyspieszenia. | |||
*Funkcje korelacji wzajemnej sygnałów o ograniczonej energii są <math>F\,</math> -transformowalne w zwykłym sensie. | |||
*Funkcje korelacji wzajemnej i widma energii wzajemnej tworzą pary transformat Fouriera. | |||
|} | |} | ||
| Linia 95: | Linia 99: | ||
|width="500px" valign="top"|[[Grafika:PS_M6_Slajd9.png]] | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd9.png]] | ||
|valign="top"| | |valign="top"| | ||
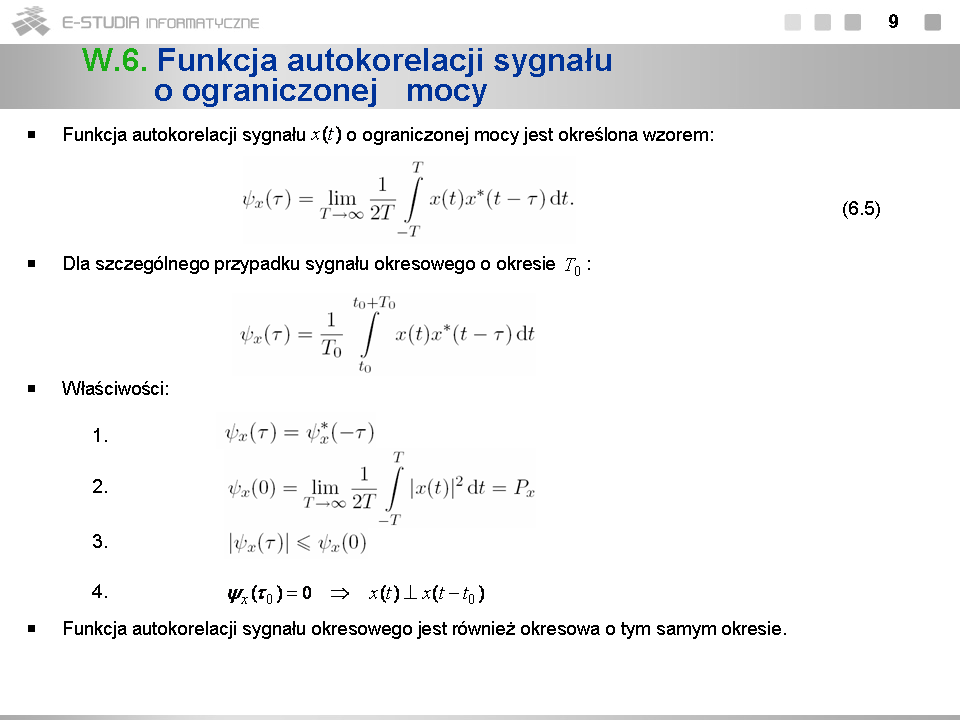
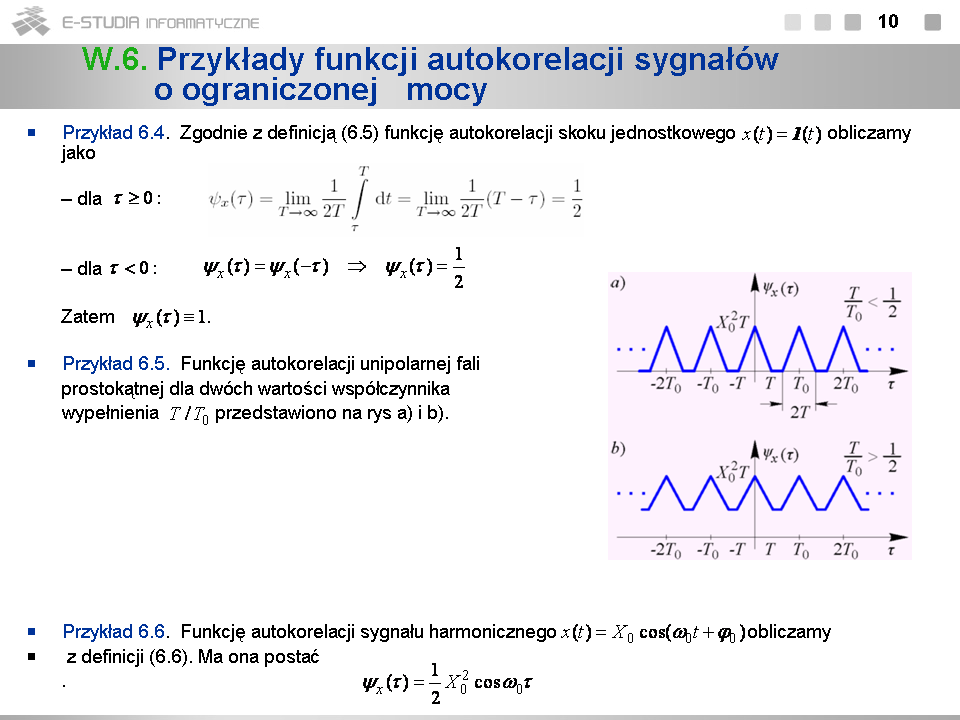
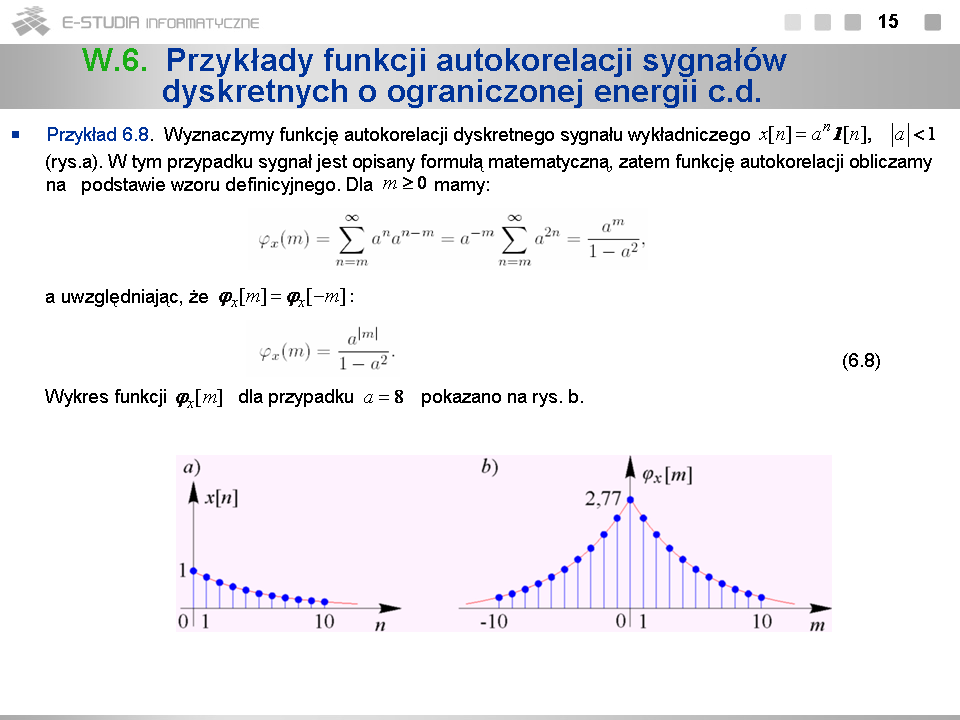
*Dla sygnałów o ograniczonej mocy funkcje korelacyjne definiujemy jako wielkości graniczne (dla odróżnienia oznaczamy je literą ''psi'') . | |||
*Właściwości funkcji autokorelacji sygnałów o ograniczonej mocy są podobne jak w przypadku sygnałów o ograniczonej energii. | |||
*Wartość funkcji autokorelacji <math>\psi_x(\tau)\,</math> sygnału o ograniczonej mocy w punkcie <math>\tau=0</math> jest rzeczywista i równa jego mocy. | |||
*Funkcja autokorelacji <math>\psi_x(\tau)\,</math> przybiera maksymalną co do modułu wartość dla <math>\tau=0</math>. | |||
*Brak korelacji czasowej sygnałów oznacza ich ortogonalność. | |||
*Funkcja autokorelacji sygnału o ograniczonej mocy jest <math>F\,</math> -transformowalna w sensie granicznym. | |||
*Funkcja autokorelacji <math>\psi_x(\tau)\,</math> jest niezmiennicza względem przesunięcia, tj. <math>\psi_x(\tau)=\psi_{x_{t_0}}(\tau)</math> dla dowolnego <math>t_0\,</math> . | |||
|} | |} | ||
Wersja z 14:54, 5 wrz 2006
|

|

|

|

|
|
|

|

|

|