|
|
| Linia 14: |
Linia 14: |
| |width="500px" valign="top"|[[Grafika:PS_M6_Slajd2.png]] | | |width="500px" valign="top"|[[Grafika:PS_M6_Slajd2.png]] |
| |valign="top"| | | |valign="top"| |
| | *Parzystość funkcji autokorelacji w przypadku sygnałów rzeczywistych oznacza, że możemy ją wówczas wyznaczać jedynie dla dodatnich wartości zmiennej <math>\tau\,</math> (opóźnień sygnału). |
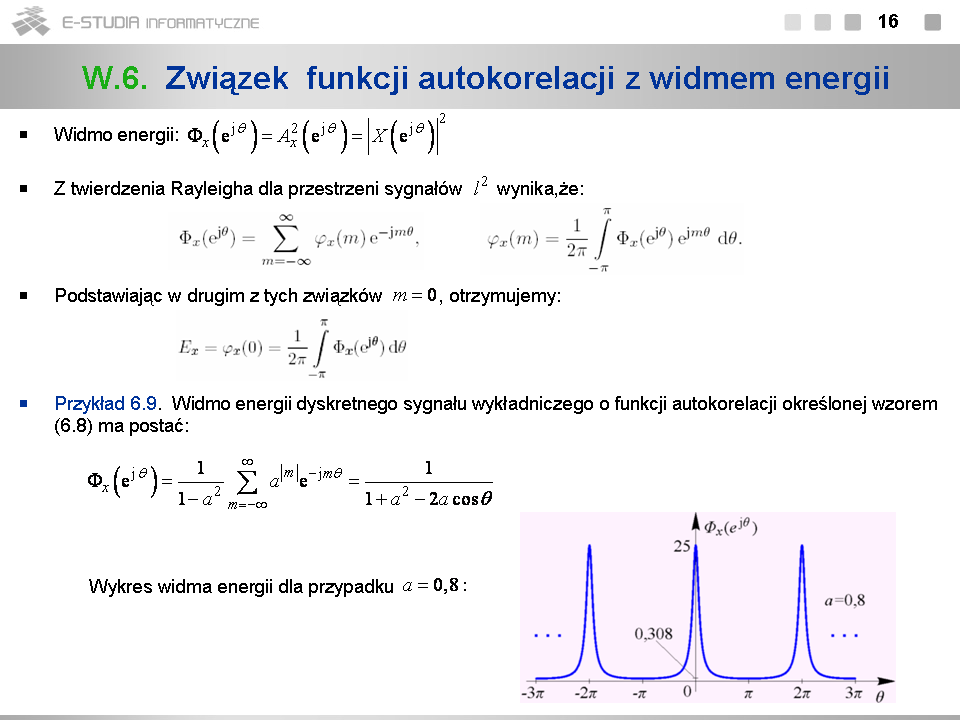
| | *Wzór (6.2) wynika z podstawienia <math>\tau=0</math> we wzorze definiującym funkcję autokorelacji. |
| | *Funkcja autokorelacji przybiera maksymalną co do modułu wartość dla <math>\tau=0</math> . |
| | *Brak korelacji czasowej sygnałów oznacza ich ortogonalność. |
| | *Funkcja autokorelacji sygnału <math>x(t)\in L^2\,</math> jest <math>F\,</math> - transformowalna w zwykłym sensie. |
| | *Funkcja autokorelacji jest niezmiennicza względem przesunięcia, tj. <math>\varphi_x(\tau)=\varphi_{x_{t_0}}(\tau)</math> dla dowolnego <math>t_0\,</math> , gdzie <math>x_{t_0}(t)=x(t-t_0)</math>. |
| | |
|
| |
|
| |} | | |} |