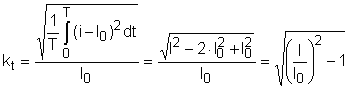Układy elektroniczne i technika pomiarowa/Moduł 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 96: | Linia 96: | ||
W literaturze wyróżnia się dwie definicje współczynnika tętnień: | W literaturze wyróżnia się dwie definicje współczynnika tętnień: | ||
<math>k_t=\frac{I'}{I_0}=\frac{U'}{U_0}</math> oraz <math>M_t=\frac{I_{0t}}{I_0}=\frac{U_{0t}}{U_0}</math> | :<math>k_t=\frac{I'}{I_0}=\frac{U'}{U_0}</math> oraz <math>M_t=\frac{I_{0t}}{I_0}=\frac{U_{0t}}{U_0}</math> | ||
gdzie: | gdzie: | ||
| Linia 109: | Linia 109: | ||
Wyrażenia te są słuszne dla dowolnego kształtu prądu odbiornika. Dla odbiornika rezystancyjnego współczynnik <math>k_t\,</math> można obliczyć ze wzoru: | Wyrażenia te są słuszne dla dowolnego kształtu prądu odbiornika. Dla odbiornika rezystancyjnego współczynnik <math>k_t\,</math> można obliczyć ze wzoru: | ||
[[Grafika:UETP_M7_Wzor1.png]] | |||
|} | |} | ||
Wersja z 11:21, 4 wrz 2006
wersja beta
UKŁADY ELEKTRONICZNE I TECHNIKA POMIAROWA
Moduł 7 - Układy zasilające
|
Wykład 7. Układy zasilające. |
|
Wprowadzenie
W niniejszym wykładzie będą omówione sposoby wytwarzania i stabilizacji napięć stałych. Każde urządzenie elektroniczne jest zasilane jednym lub kilkoma napięciami stałymi. Przy dużych zapotrzebowaniach na energię elektryczną stosowanie baterii lub akumulatorów jest nieekonomiczne. Napięcia stałe wytwarza się przez transformowanie i prostowanie napięcia sieciowego jedno lub trójfazowego. Uzyskane w ten sposób napięcie zawiera najczęściej znaczne tętnienia. Zatem, aby można korzystać z takiego zasilacza należy zastosować odpowiednie filtry tętnień. Ponadto, ponieważ napięcie wyprostowane zmienia się wraz ze zmianami napięcia w sieci zasilającej oraz pod wpływem zmian obciążenia na wyjściu prostownika często jest dołączony układ stabilizatora napięcia. |
|
Klasyczny układ zasilacza składa się z czterech podstawowych elementów: transformatora sieciowego, prostownika, filtru i jeżeli to jest potrzebne ze stabilizatora napięcia lub rzadziej prądu. |
|
Transformatory przekształcające napięcie sieciowe na napięcie o innej, najczęściej mniejszej wartości niż napięcie sieci zasilającej nazywamy transformatorami sieciowymi. Transformatory sieciowe są zasilane przebiegami sinusoidalnymi
o częstotliwości 50 Hz. |
|
Prostowniki sieciowe niesterowane
W zależności od liczby faz zasilających układ wyróżnia się:
W zależności od liczby pulsów napięcia wyjściowego prostownika w jednym okresie napięcia zasilającego układ wyróżnia się,
Ze względu na topologię układu prostownika wyróżnia się:
|
|
Prostowniki sieciowe sterowane buduje się zastępując diody prostownicze w układach niesterowanych, tyrystorami. |
|
Prostowniki jednofazowe. Przy obciążeniu rezystancyjnym kształty przebiegów prądu odbiornika i napięcia na jego zaciskach są identyczne, a każda dioda w układzie prostownika przewodzi przez pół okresu zmienności przebiegu napięcia zasilania. |
|
Filtry tętnień
W celu zmniejszenia amplitudy napięcia tętnień na zaciskach odbiornika, a co za tym idzie także amplitudy tętnień prądu odbiornika, pomiędzy prostownik i odbiornik włącza się filtr tętnień. Zadaniem filtru jest zmniejszenie wartości składowej zmiennej w przebiegu napięcia wyprostowanego. W filtrach wykorzystuje się właściwości akumulowania energii przez elementy inercyjne: kondensator w polu elektrycznym i dławik indukcyjny w polu magnetycznym.
|
|
Parametry filtrów prostowniczych
W literaturze wyróżnia się dwie definicje współczynnika tętnień:
gdzie:
Wyrażenia te są słuszne dla dowolnego kształtu prądu odbiornika. Dla odbiornika rezystancyjnego współczynnik można obliczyć ze wzoru:
|
|
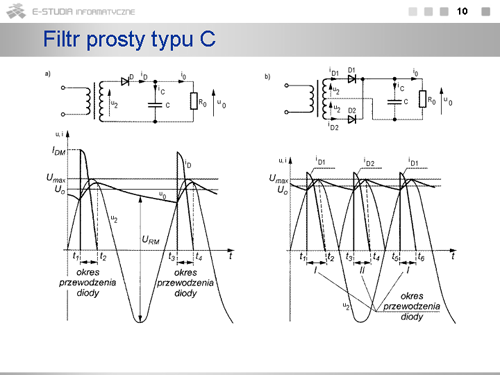
opis |
|
opis |
|
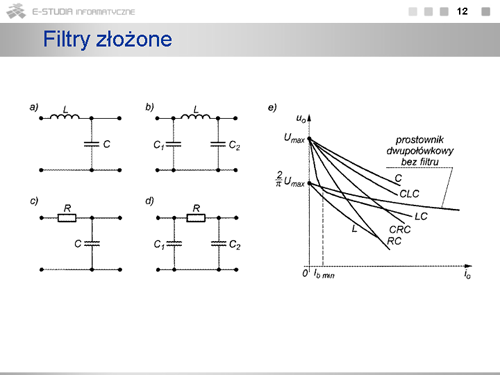
opis |
|
opis |
|
opis |
|
opis |
|
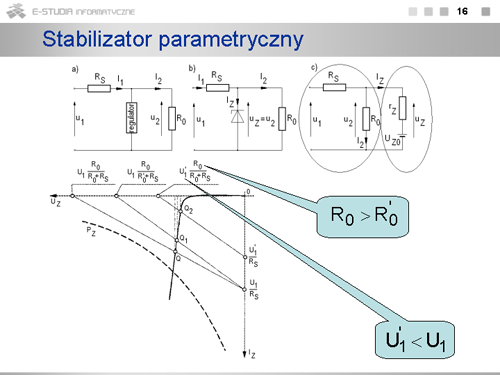
opis |
|
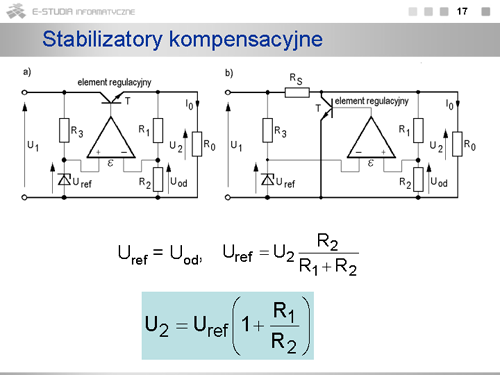
opis |
|
opis |
|
opis |
|
opis |
|
|
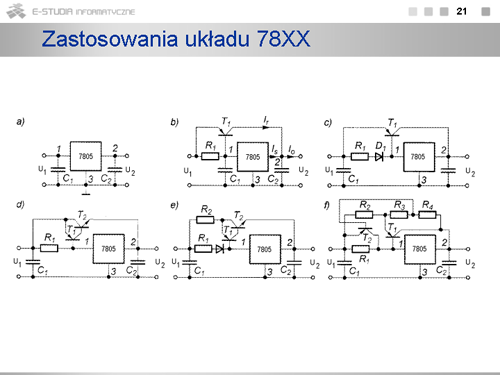
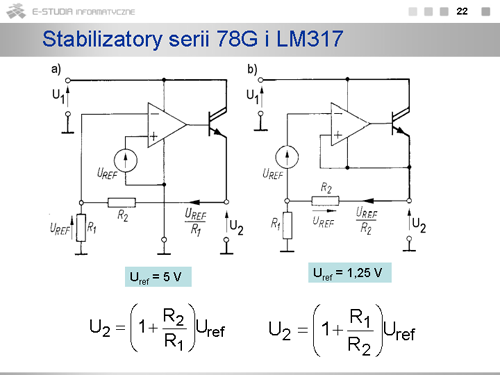
opis |
|
opis |
</math>
