Teoria informacji/TI Wykład 5

Entropia warunkowa i informacja wzajemna

Definicja [Entropia zmiennej losowej]

Jeśli $X:S\to {𝒳}$ jest zmienną losową, określamy jej entropię jako

$H_r(X)=\sum _{t\in {𝒳}}p(X=t)\cdot {\log }_r\frac{1}{p(X=t)}$

Innymi słowy, $H_r(X)$ jest równe wartości oczekiwanej

$H_r(X)=E\left({\log }_r\frac{1}{p(X)}\right)$

gdzie p(X) jest zmienną losową na S zdefiniowaną jako $p(X):s\mapsto p(X=X(s))$

$\sum _{t\in {𝒳}}p(X=t)\cdot {\log }_r\frac{1}{p(X=t)}=\sum _{t\in {𝒳}}\sum _{X(s)=t}p(s)\cdot \frac{1}{p(X=t)}=\sum _{s\in S}p(s)\cdot \frac{1}{p(X=X(s))}$

Umowa notacyjna Jeśli zmienne losowe o których mowa będą wynikały z kontekstu, często będziemy omijać zapis $X=a$ i pisać po prostu a. Przykładowo będziemy pisać p(x|y) zamiast $p(X=x|Y=y)$, $p(x\wedge y)$ zamiast $p((X=x)\wedge (Y=y))$ itp.

Definicja [Entropia warunkowa]

Niech $A:S\to {𝒜}$,$B:S\to {ℬ}$ będą dwiema zmiennymi losowymi. Dla $b\in {ℬ}$ określamy $H_r(A|b)=\sum _{a\in {𝒜}}p(a|b)\cdot {\log }_r\frac{1}{p(a|b)}$

i ogólnie

$H_r(A|B)=\sum _{b\in {ℬ}}p(b)H_r(A|b)$. Powyższą wartość nazywamy entropią warunkową A od B

Zauważmy że jeśli A i B są niezależne, to w powyższej formule $p(a|b)=a$ a więc $H_r(A|B)=A$. Z drugiej strony $H_r(A|A)=0$. Ogólnie dla dowolnej funkcji $\phi :{𝒜}\to {ℬ}$ mamy

$H_r(\phi (A)|A)=0$

Rzeczywiście, jeśli $p(A=a)>0$ to $p(\phi (A)=\phi (a)|A=a)=1$, i w konsekwencji ${\log }_r\frac{1}{p(\phi (A)=\phi (a)|A=a)}=0$.

Entropia łączna Będziemy również rozważać pary (A,B) jako jedną zmienną losową $(A,B):S\to {𝒜}\times {ℬ}$,

$(A,B)(s)=(A(s),B(s))$

Prawdopodobieństwo że ta zmienna przyjmie wartość (a,b) wynosi $p((A,B)=(a,b))=p((A=a)\wedge (B=b))$, co zapisujemy w skrócie jako $p(a\wedge b)$. To prawdopodobieństwo w ogólności jest inne niż $p(a)\cdot p(b)$. Jeśli dla dowolnych $a\in {𝒜},b\in {ℬ}$ $p(a\wedge b)=p(a)\cdot p(b)$, mówimy że zmienne losowe A i B są niezależne.

Entropia $H_r(A,B)$ wprost z definicji wynosi

$H_r(A,B)=\sum _{a\in {𝒜},b\in {ℬ}}p(a\wedge b)\cdot {\log }_r\frac{1}{p(a\wedge b)}$

Jeśli A i B są niezależne, to

${\log }_r\frac{1}{p(A,B)}={\log }_r\frac{1}{p(A)}+{\log }_r\frac{1}{p(B)}$

Z liniowości wartości oczekiwanej dostajemy wtedy

$H_r(A,B)=H_r(A)+H_r(B)$

W ogólnym przypadku możemy udowodnić:

Twierdzenie

Dla dowolnych A i B zachodzi $H_r(A,B)\le H_r(A)+H_r(B)$ i równość zachodzi jedynie gdy A i B są niezależne.

Dowód

Rozpiszemy prawą stronę tak żebyśmy mogli użyć Złotego Lematu. Użyjemy w tym celu oczywistych równości

$p(a)=\sum _{b\in {ℬ}}p(a\wedge b)$ i $p(b)=\sum _{a\in {𝒜}}p(a\wedge b)$.

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \aligned H_r (A) + H_r (B) & = \sum_{a \in {\mathcal A}} p (a) \log_r \frac{1}{p(a)} + \sum_{b \in {\mathcal B}} p(b) \log_r \frac{1}{p(b)}\\ & = \sum_{a \in {\mathcal A}} \sum_{b \in {\mathcal B}} p( a \wedge b) \log_r \frac{1}{p(a)} + \sum_{b \in {\mathcal B}} \sum_{a \in {\mathcal A}} p( a \wedge b) \log_r \frac{1}{p(b)}\\ & = \sum_{a \in {\mathcal A}, b \in {\mathcal B}} p( a \wedge b) \log_r \frac{1}{p(a)p(b)} \endaligned }

Ważne że powyższe wyrażenie jest dobrze zdefiniowane, bo gdy $p(a)=0$ lub $p(b)=0$, to również $p(a\wedge b)=0$.

Oznaczmy chwilowo

$({𝒜}\times {ℬ}{)}^{+}=\{(a,b):p(a)>0\text{ i }p(b)>0\}$

Mamy wtedy

$\sum _{(a,b)\in ({𝒜}\times {ℬ}{)}^{+}}p(a\wedge b)=\sum _{(a,b)\in ({𝒜}\times {ℬ}{)}^{+}}p(a)\cdot p(b)=1$.

Używając Złotego Lematu dla $x=p(a\wedge b)$, $y=p(a)\cdot p(b)$ dla wszystkich $(a,b)\in ({𝒜}\times {ℬ}{)}^{+}$ otrzymujemy

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \aligned H_r (A,B) & = \sum_{ (a,b) \in ({\mathcal A} \times {\mathcal B})^{+}} p( a \wedge b) \log_r \frac{1}{p( a \wedge b)}\\ & \leq \sum_{ (a,b) \in ({\mathcal A} \times {\mathcal B})^{+}} p( a \wedge b) \log_r \frac{1}{p(a)p(b) }\\ & = H_r (A) + H_r (B) \endaligned } Dodatkowo równość zachodzi wyłącznie gdy $p(a\wedge b)=p(a)\cdot p(b)$ dla wszystkich $(a,b)\in ({𝒜}\times {ℬ}{)}^{+}$ (czyli w ogóle dla wszystkich $a\in {𝒜},b\in {ℬ}$. W drugą stronę, wiemy już że niezależność A i B implikuje tutaj równość.

Definicja [Informacja]

Wartość $I(A;B)=H_r(A)+H_r(B)-H_r(A,B)$ nazywamy informacją wzajemną zmiennych A i B.

Komentarz Powyższę definicję łatwo zrozumieć w odniesieniu do Gry w 20 pytań. Przypuścmy że mamy zidentyfikować obiekt który jest parą (a,b) gdzie a i b są wartościami zmiennych losowych A i B. Jeśli A i B są niezależne, najlepsze co możemy zrobić to zidentyfikować niezależnie a i b. Tym samym gramy w dwie niezależne gry „pytania o a” i „pytania o b” (co odpowiada równości $H_r(A,B)=H_r(A)+H_r(B)$). Jeśli jednak A i B są zależne, możemy wykorzystać tę wzajemną informację do zmniejszenia liczby pytań.

Dla zwiększenia czytelności tekstu, od tej pory będziemy zwykle omijać dolny indeks r, pisząc H, I, itp. Wszędzie tam gdzie nie napisano inaczej, wszystkie twierdzenia odnoszą się do przypadku dowolnego $r>1$. Bez utraty ogólności czytelnik może założyć r=2.

Komentarz Przekształcając definicję informacji analogicznie jak w ostatnim dowodzie, otrzymujemy:

$I(A;B)=\sum _{a\in {𝒜},b\in {ℬ}}p(a\wedge b)(\log \frac{1}{p(a)p(b)}-\log \frac{1}{p(a\wedge b)})$

W takiej postaci widać że informacja jest pewną miarą odległości pomiędzy faktycznym rozkładem zmiennej (A;B), a jej rozkładem gdyby A i B były niezależne.

Warto zauważyć że powyższa suma jest nieujemna, choć niektóre składniki $(\log \frac{1}{p(a)p(b)}-\log \frac{1}{p(a\wedge b)})$ mogą być ujemne.

Istnieje odpowiednik równości $H(A,B)=H(A)+H(B)$, który stosuje się do zmiennych zależnych:

Fakt [Zasada łańcuchowa]

Dla dowolnych A i B zachodzi $H(A,B)=H(A|B)+H(B)$

Dowód

Obliczamy: Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \aligned H(A,B) & = \sum_{a \in {\mathcal A}, b \in {\mathcal B}} p ( a \wedge b) \cdot \log \frac{1}{p( a \wedge b)}\\ & = \sum_{a \in {\mathcal A}} \sum_{b \in {\mathcal B}} p(a|b) p(b) \cdot \log \frac{1}{p(a|b) p(b)} \\ & = \sum_{a \in {\mathcal A}} \sum_{b \in {\mathcal B}} p(a|b) p(b) \cdot \left( \log \frac{1}{p(a|b)} + \log \frac{1}{p(b)} \right)\\ & = \sum_{b \in {\mathcal B}} p(b) \cdot \sum_{a \in {\mathcal A}} p(a|b) \cdot \log \frac{1}{p(a|b)} + \sum_{b \in {\mathcal B}} p(b) \log \frac{1}{p(b)} \cdot \sum_{a \in {\mathcal A}} p(a|b) \\ & = H(A|B) + H(B) \endaligned }

Używając zasady łańcuchowej, możemy wyliczać informację na różne sposoby:

$I(A;B)=H(A)-H(A|B)=H(B)-H(B|A)$

Kolejną rzeczą jaką możemy zauważyć to $I(A;B)\le \min \{H(A),H(B)\}$

Łatwo możemy też uogólnić zasadę łańcuchową na przypadek $n\ge 2$ zmiennych $A_1,A_2,\dots ,A_n$

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \aligned H(A_1, \ldots , A_n ) & = H(A_1 | A_2, \ldots , A_n ) + H(A_2, \ldots , A_n ) \\ & = H(A_1 | A_2, \ldots , A_n ) + H(A_2 | A_3 , \ldots , A_n) + H(A_3, \ldots , A_n)\\ & = \sum_{i = 1}^n H(A_i | A_{i+1} , \ldots , A_n) \endaligned }

(przyjmujemy konwencję $H(A|\mathrm{\varnothing })=H(A)$)

Bardziej wyrafinowane uogólnienie możemy uzyskać stosując entropię warunkową:

Fakt [Warunkowa zasada łańcuchowa]

Dla dowolnych A, B i C zachodzi $H(A,B|C)=H(A|B,C)+H(B|C)$

Dowód

Dla dowolnego $c\in {𝒞}$ rozwijamy Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \aligned H(A,B| c) & = \sum_{a \in {\mathcal A}, b \in {\mathcal B}} p ( a \wedge b | c) \cdot \log \frac{1}{p( a \wedge b| c )}\\ & = \sum_{a, b} p (a | b \wedge c) \cdot p(b|c) \cdot \left( \log \frac{1}{p (a | b \wedge c)} + \log \frac{1}{p (b|c) } \right)\\ & = \sum_{b} p(b|c) \cdot \sum_{a} p (a | b \wedge c) \cdot \log \frac{1}{p (a | b \wedge c)} + \sum_{b} p(b|c) \cdot \log \frac{1}{p (b|c) } \cdot \underbrace{\sum_{a} p (a | b \wedge c)}_{=1} \endaligned }

W powyższym wyliczeniu sumy po a i b obejmują te wartości, dla których odpowiednie prawdopodobieństwa zależne są zdefiniowane ($p(x|y)$ nie jest określone jeśli $p(y)=0$).

Używamy tu łatwego faktu, że jeśli $p(a\wedge b|c)>0$, to

$p(a\wedge b|c)=\frac{p(a\wedge b\wedge c)}{p(c)}=\frac{p(a\wedge b\wedge c)}{p(b\wedge c)}\cdot \frac{p(b\wedge c)}{p(c)}=p(a|b\wedge c)\cdot p(b|c)$

Uśredniając po $p(c)$ dostajemy:

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \aligned H(A,B|C) & = \sum_{c \in {\mathcal C}} p(c) \cdot H (A,B | c)\\ & = \sum_{c} p(c) \cdot \sum_{b} p(b|c) \cdot \sum_{a} p (a | b \wedge c) \cdot \log \frac{1}{p (a | b \wedge c)} + \sum_{c} p(c) \cdot \sum_{b} p(b|c) \cdot \log \frac{1}{p (b|c) }\\ & = \underbrace{\sum_{b,c} p(b \wedge c) \cdot \sum_{a} p (a | b \wedge c) \cdot \log \frac{1}{p (a | b \wedge c)}}_{=H(A| B,C)} + \underbrace{\sum_{c} p(c) \cdot \sum_{b} p(b|c) \cdot \log \frac{1}{p (b|c) }}_{=H (B | C)} \endaligned }

Definicja [Informacja warunkowa]

Definiujemy informację wzajemną A i B warunkowaną przez C jako

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \aligned I(A;B |C) & = H(A |C) + H(B|C) - \underbrace{H(A,B|C)}_{=H(A|B,C) + H(B|C)} \\ & = H(A |C) - H(A|B,C) \endaligned }

I wreszcie, informację wzajemną A, B i C definiujemy jako:

$R(A;B;C)=I(A;B)-I(A;B|C)$

Łatwo sprawdzimy że ta definicja jest rzeczywiście symetryczna, tzn nie zależy od kolejności A, B i C:

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \aligned I(A;C) - I(A;C|B) = H(A) - H(A|C) - \left( H (A|B) - H(A| B,C) \right) \\ & = \underbrace{H(A) - H (A|B)}_{=I(A;B)} - \underbrace{ H(A|C) - H(A| B,C)}_{=I(A;B |C)} \endaligned }

Należy jednak pamiętać że w przeciwieństwie do $I(A;B)$ i $I(A;B|C)$, zdefiniowana powyżej $R(A;B;C)$ może mieć ujemną wartość.

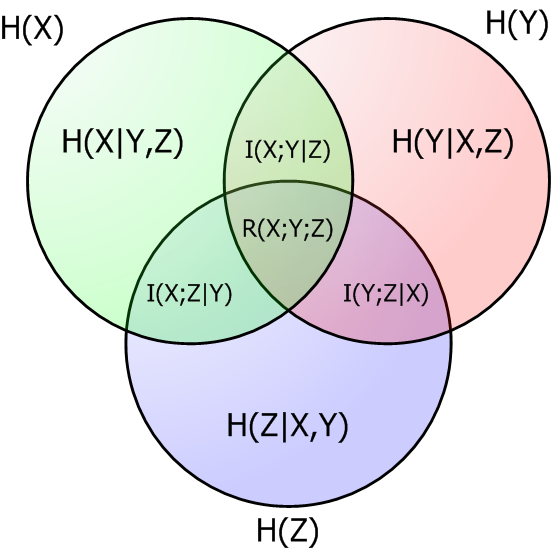
Zależności pomiędzy wartościami $H(X),H(Y),H(Z),H(X,Y),H(X,Y|Z),I(X;Y),I(X;Y|Z),R(X;Y;Z)$ itd. można przedstawić w postaci diagramu: