ED-4.2-m12-1.0-Slajd19: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 4: | Linia 4: | ||
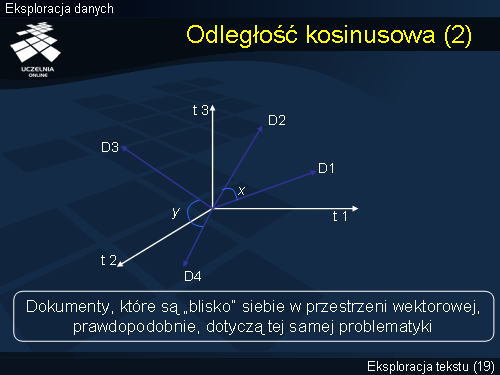
Prezentowany slajd ilustruje ideę miary kosinusowej. Dane są 3 słowa kluczowe t1, t2, i t3, oraz 4 dokumenty reprezentowane przez wektory D1, D2, D3 i D4. Jeżeli kosinus kąta pomiędzy wektorami reprezentującymi dwa dokumenty jest bliski 0, wówczas kosinus kąta zmierza do 1. Takie dokumenty leżą | Prezentowany slajd ilustruje ideę miary kosinusowej. Dane są 3 słowa kluczowe t1, t2, i t3, oraz 4 dokumenty reprezentowane przez wektory D1, D2, D3 i D4. Jeżeli kosinus kąta pomiędzy wektorami reprezentującymi dwa dokumenty jest bliski 0, wówczas kosinus kąta zmierza do 1. Takie dokumenty leżą „blisko” siebie w przestrzeni wektorowej, i, prawdopodobnie, dotyczą tej samej problematyki. | ||
[[ED-4.2-m12-1.0-Slajd18 | << Poprzedni slajd]] | [[ED-4.2-m12-1.0-toc|Spis treści ]] | [[ED-4.2-m12-1.0-Slajd20 | Następny slajd >>]] | [[ED-4.2-m12-1.0-Slajd18 | << Poprzedni slajd]] | [[ED-4.2-m12-1.0-toc|Spis treści ]] | [[ED-4.2-m12-1.0-Slajd20 | Następny slajd >>]] | ||
Aktualna wersja na dzień 12:53, 31 sie 2006
Odległość kosinusowa (2)
Prezentowany slajd ilustruje ideę miary kosinusowej. Dane są 3 słowa kluczowe t1, t2, i t3, oraz 4 dokumenty reprezentowane przez wektory D1, D2, D3 i D4. Jeżeli kosinus kąta pomiędzy wektorami reprezentującymi dwa dokumenty jest bliski 0, wówczas kosinus kąta zmierza do 1. Takie dokumenty leżą „blisko” siebie w przestrzeni wektorowej, i, prawdopodobnie, dotyczą tej samej problematyki.