PEE Moduł 3: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 145: | Linia 145: | ||
|} | |} | ||
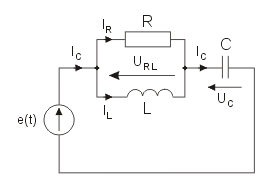
Niech dany będzie obwód RLC o strukturze przedstawionej na rysunku zasilany z sinusoidalnego źródła napięcia <math>e(t)=100\sqrt 2 sin(\omega t+45^o)</math> V o wartości <math>\omega=1\frac{rad}{s}</math> Wartości elementów obwodu są następujące: <math>R=1\Omega , C=0,5F, L=1H</math> | Niech dany będzie obwód RLC o strukturze przedstawionej na rysunku zasilany z sinusoidalnego źródła napięcia <math>e(t)=100\sqrt 2 sin(\omega t+45^o)</math> V o wartości <math>\omega=1\frac{rad}{s}</math>. Wartości elementów obwodu są następujące: <math>R=1\Omega , C=0,5F, L=1H</math>. | ||
Należy wyznaczyć wartości skuteczne zespolone prądów i napięć elementów oraz moce i bilans mocy w obwodzie. | Należy wyznaczyć wartości skuteczne zespolone prądów i napięć elementów oraz moce i bilans mocy w obwodzie. | ||
| Linia 154: | Linia 154: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd11.png]] | ||
|valign="top"| | |valign="top"|''Rozwiązanie'' | ||
Wartości zespolone impedancji i napięcia wymuszającego w obwodzie przy danych wartościach elementów są równe: | Wartości zespolone impedancji i napięcia wymuszającego w obwodzie przy danych wartościach elementów są równe: | ||
: <math>Z_L=j\omega L=j1, Z_C=-j1/\omega C=-j2, E=100e^j^{45^o}</math> | |||
<math>Z_L=j\omega L=j1, Z_C=-j1/\omega C=-j2, E=100e^j^{45^o}</math> | |||
Impedancja zastępcza połączenia równoległego L i R równa się | Impedancja zastępcza połączenia równoległego L i R równa się | ||
: <math>Z_R_L=\frac{RZ_L}{R+Z_L}=0,707e^j^{45^o}</math> | |||
<math>Z_R_L=\frac{RZ_L}{R+Z_L}=0,707e^j^{45^o}</math> | |||
Impedancja zastępcza połączenia szeregowego <math>Z_C</math> i <math>Z_{RL}</math> jest równa | Impedancja zastępcza połączenia szeregowego <math>Z_C</math> i <math>Z_{RL}</math> jest równa | ||
: <math>Z=Z_C+Z_{RL}=-j2 + 0,5 + j0,5 = 1,58e^{-j 71,6^o}</math> | |||
<math>Z=Z_C+Z_{RL}=-j2 + 0,5 + j0,5 = 1,58e^{-j 71,6^o}</math> | |||
|} | |} | ||
| Linia 178: | Linia 173: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd12.png]] | ||
|valign="top"| | |valign="top"|Napięcia na poszczególnych elementach obwodu dane są w postaci | ||
Napięcia na poszczególnych elementach obwodu dane są w postaci | |||
<math> | : <math>I_C = \frac{E}{Z} = \frac{100e^{j45^o}}{1,58e^{-j71,6^o}} = 63,3 e^{j116,6^o}</math> | ||
: <math>U_C=Z_CI_C=126,6e^j^{26,6^o}</math> | |||
<math>U_R_L=Z_R_L I_C=44,72e^j^{161,6^o}</math> | : <math>U_R_L=Z_R_L I_C=44,72e^j^{161,6^o}</math> | ||
Prądy cewki i rezystora obliczone z prawa Ohma równają się | Prądy cewki i rezystora obliczone z prawa Ohma równają się | ||
: <math>I_L=\frac{U_R_L}{Z_L}=44,72e^j^{71,6^o}</math> | |||
: <math>I_R=\frac{U_R_L}{R}=44,72e^j^{161,6^o}</math> | |||
<math>I_R=\frac{U_R_L}{R}=44,72e^j^{161,6^o}</math> | |||
|} | |} | ||
| Linia 208: | Linia 194: | ||
|valign="top" width="500px"|[[Grafika:PEE_M3_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M3_Slajd13.png]] | ||
|valign="top"| | |valign="top"| | ||
Na rysunku przedstawiono wykres wektorowy prądów i napięć w obwodzie. | Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie. | ||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M3_rys3_3_animacja.gif]] | |||
|} | |||
|} | |} | ||
Wersja z 08:50, 30 sie 2006

|
Wykład 3. Zagadnienia mocy w obwodach RLC przy wymuszeniu sinusoidalnym |
| <applet code="moce_demo.class" archive="images/a/a9/PEE_M3_moce.jar" width="600" height="580"></applet> | Umieszczony obok program pozwala na analizę w trybie on-line obwodu RLC o strukturze przedstawionej na rysunku. Użytkownik wybiera elementy obwodu włączone w strukturę i wpisuje ich wartości. Po naciśnięciu przycisku OBLICZ program automatycznie obliczy wartości wszystkich prądów, napięć i mocy elementów, podając jednocześnie bilans mocy. |

|
Rozwiązanie
Wartości zespolone impedancji i napięcia wymuszającego w obwodzie przy danych wartościach elementów są równe: Impedancja zastępcza połączenia równoległego L i R równa się Impedancja zastępcza połączenia szeregowego i jest równa |

|
Napięcia na poszczególnych elementach obwodu dane są w postaci
|

|
Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie.
|

|
Poszczególne rodzaje mocy wydzielonej w obwodzie równają się:
|

|
Energia magazynowana w idealnym kondensatorze
Cewka i kondensator traktowane jako idealne elementy obwodowe należą do elementów magazynujących energię elektryczną. Rozpatrzmy kondensator o pojemności zasilony z generatora napięciowego . Obliczymy energię dostarczoną do tego kondensatora w czasie od do . Energia ta może być obliczona jako całka z mocy chwilowej
Uwzględniając wzór na moc chwilową i dokonując odpowiednich operacji całkowania otrzymujemy
Uwzględniając wzór na moc chwilową i dokonując odpowiednich operacji całkowania otrzymujemy
Zasadniczą cechą kondensatora idealnego jest jego bezstratność, co oznacza, że energia zgromadzona na nim pozostaje w nim zmagazynowana. Zatem kondensator naładowany do napięcia stałego U posiada energię równą
Jest to bardzo ważna własność kondensatora, wykorzystywana do magazynowania energii elektrycznej. |

|
Energia magazynowana w idealnej cewce
Rozpatrzmy cewkę o indukcyjności zasiloną z generatora napięciowego . Obliczymy energię dostarczoną do tej cewki w czasie od do . Energia ta, podobnie jak w przypadku kondensatora, może być obliczona jako całka z mocy chwilowej
Uwzględniając wzór na moc chwilową i dokonując odpowiednich operacji całkowania otrzymujemy
Załóżmy, że czas t0 jest taką chwilą, w której prąd cewki jest zerowy. W takim razie wzór na energię upraszcza się do postaci
Zasadniczą cechą cewki idealnej jest jej bezstratność, co oznacza, że energia dostarczona do niej pozostaje w niej zmagazynowana. Zatem cewka, przez która przepływa prąd stały I posiada energię równą
W odróżnieniu od kondensatora, w którym energia związana była z napięciem między okładkami (ładunkiem) energia cewki jest uzależniona od prądu (strumienia magnetycznego). Stąd przyjmuje się, że kondensator magazynuje energię w polu elektrycznym a cewka w polu magnetycznym. |
| Zadania sprawdzające
Zadanie 3.1 Sporządzić bilans mocy w obwodzie przedstawionym na rysunku. Przyjąć następujące wartości elementów:
Wartości symboliczne elementów obwodu:
Parser nie mógł rozpoznać (nieznana funkcja „\omegaL”): {\displaystyle Z_L=j\omegaL=j10}
Moc odbiornika jest dokładnie równa mocy źródła.
|