TC Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 161: | Linia 161: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd17.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd17.png]] | ||
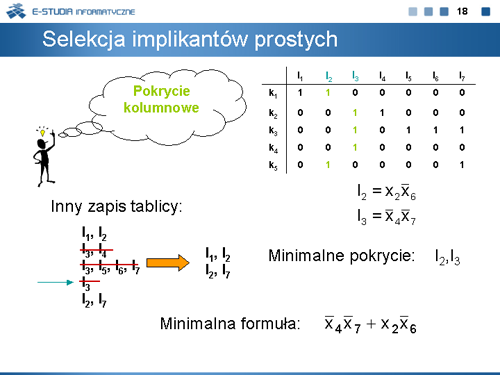
|valign="top"| | |valign="top"|Tablicę implikantów prostych konstruujemy w następujący sposób. Jeśli implikant <math>I_j\,</math> pokrywa kostkę <math>k_i\,</math> , to na przecięciu wiersza wiersza <math>k_i\,</math> z kolumną <math>I_j\,</math> piszemy 1, w przeciwnym przypadku piszemy 0. | ||
Tablica implikantów prostych umożliwia wybór (selekcję) takiego minimalnego zbioru implikantów, który pokrywa wszystkie kostki funkcji pierwotnej | |||
|} | |} | ||
| Linia 168: | Linia 171: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd18.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd18.png]] | ||
|valign="top"| | |valign="top"|Minimalny zbiór implikantów prostych reprezentujących funkcję <math>f\,</math> można wyznaczyć obliczając minimalne pokrycie kolumnowe tablicy implikantów prostych. W tym celu zapisujemy wiersze tablicy w postaci zbiorów kolumn wskazywanych przez pozycje jedynek w danym wierszu, a następnie zauważając, że implikant <math>I_3\,</math> tworzy zbiór jednoelementowy wykreślamy wiersze z tym implikantem. Po takiej redukcji wierszy spostrzegamy, że I2 jest wspólny dla obu wierszy. Zatem minimalne pokrycie tworzą implikanty <math>I_2\,</math> , <math>I_3\,</math>. Czyli <math>f=\overline{x}_4\overline{x}_7+x_2\overline{x}_6</math> . | ||
|} | |} | ||
| Linia 175: | Linia 179: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd19.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd19.png]] | ||
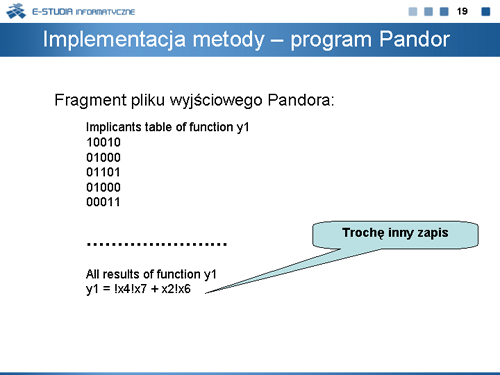
|valign="top"| | |valign="top"|Analogiczny wynik obliczy program PANDOR. | ||
Pandor jest akademickim narzędziem minimalizacji funkcji boolowskich zmodyfikowaną metodą ekspansji z zastosowaniem dodatkowej procedury redukcji argumentów. Pandor został opracowany w ramach pracy dyplomowej Mirosława Cagary w Ośrodku Kształcenia na Odległość OKNO Politechniki Warszawskiej. Program Pandor jest dostępny na stronie internetowej www.zpt.tele.pw.edu.pl, a także na stronie internetowej jego autora www.domicil.pl. | |||
|} | |} | ||
| Linia 182: | Linia 189: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd20.png]][[Grafika:TC_M4_Slajd21.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd20.png]][[Grafika:TC_M4_Slajd21.png]] | ||
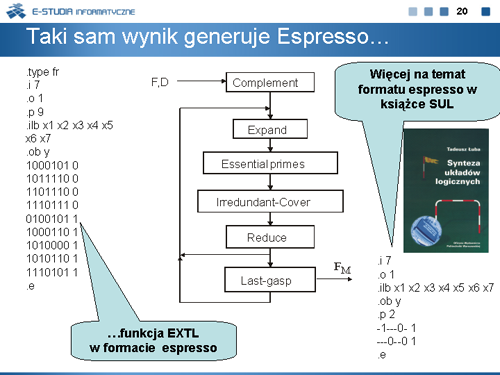
|valign="top"| | |valign="top"|Również program ESPRESSO obliczy taki sam wynik. Zapis funkcji EXTL w standardzie Espresso podano na planszach 20 i 21. Więcej informacji na temat standardu Espresso można znaleźć w książce ''Synteza układów logicznych''. | ||
Taki sam wynik minimalizacji funkcji EXTL w programie PANDOR (wyposażonym tylko w jedną procedurę ekspansji) oraz w programie ESPRESSO (zbudowanym z wielu procedur) nasuwa wątpliwości. Dlaczego program PANDOR za pomocą jednej procedury minimalizuje tak samo dobrze jak ESPRESSO zbudowane z wielu procedur. | |||
|} | |} | ||
| Linia 190: | Linia 200: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd22.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd22.png]] | ||
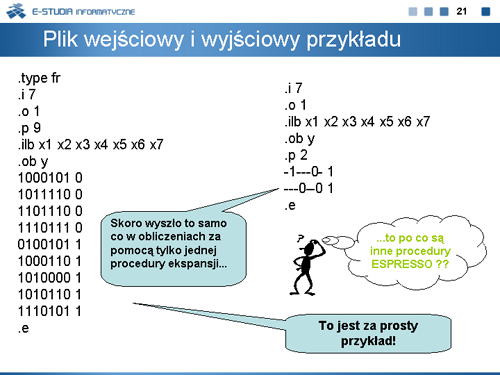
|valign="top"| | |valign="top"|Barierą ograniczającą obliczenia systematyczną metodą zastosowaną w Pandorze jest ogromna złożoność obliczeniowa zarówno w procesie generacji, jak też w procesie obliczania pokrycia kolumnowego. | ||
Program PANDOR został stworzony po to, aby naocznie zaobserwować zjawisko wzrostu złożoności obliczeniowej wraz ze wzrostem liczby argumentów funkcji. | |||
Funkcja EXTL ma 7 implikantów (Pandor dokonuje lepszej selekcji i oblicza ich zaledwie 5). W tym przypadku obliczenie minimalnego pokrycia kolumnowego jest zadaniem łatwym. Ale już dla bardziej skomplikowanych funkcji takich jak TL27 i KAZ, których tablice w standardzie Espresso są podane na planszy, sytuacja jest całkiem inna – właśnie ze względu na dużą liczbę implikantów. Czas obliczeń programem PANDOR jest drastycznie większy od czasu obliczeń programem Espresso. Oczywiście Espresso nie zawsze poda wynik minimalny. W celu uzyskania minimalnych rozwiązań w rozsądnym czasie obliczeń w programie PANDOR zastosowano procedurę redukcji argumentów. Jej wpływ na proces minimalizacji omówimy w następnym wykładzie. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 23:20, 28 sie 2006

|
Minimalizacja funkcji boolowskich metodą ekspansji. |

|
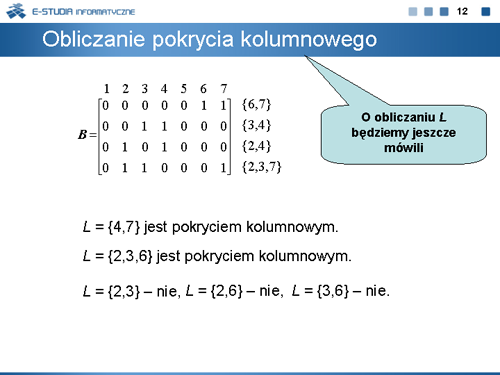
Pokryciem kolumnowym macierzy , , jest zbiór taki, że dla każdego istnieje , dla którego . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje , który jest pokryciem macierzy . |
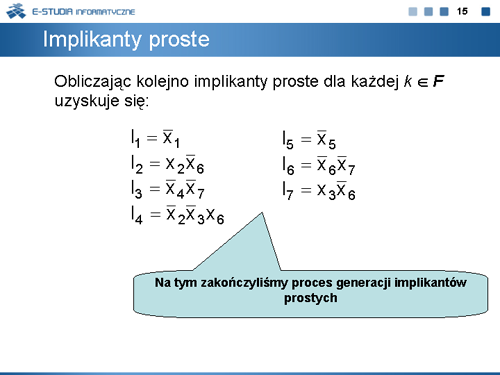
|

|