TC Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 119: | Linia 119: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M4_Slajd13.png]] | |valign="top" width="450px"|[[Grafika:TC_M4_Slajd13.png]] | ||
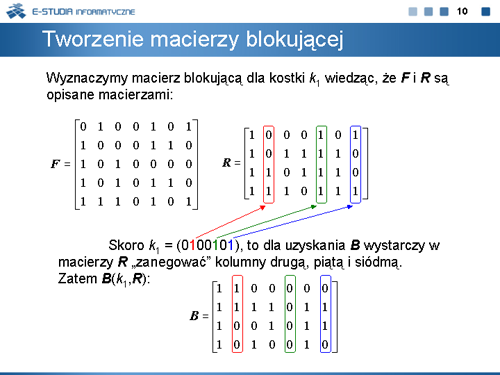
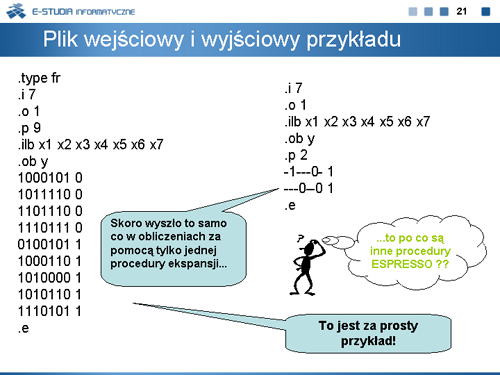
|valign="top"| | |valign="top"|Macierz blokująca <math>B(k,R)\,</math> pozwala wyznaczyć rozwinięcie (ekspansję) kostki <math>k\,</math> oznaczane <math>k^{+}(L,k)\,</math> w sposób następujący: | ||
<math>k^{+}_j = \begin{cases}k_j & ,gdy\, j\,\epsilon\, L \\ * & ,w\, pozostalych\, przypadkach \end{cases}</math> | |||
Można wykazać, że <math>k^{+}(L,k)\,</math> jest implikantem funkcji <math>f=(F,R)\,</math>. W szczególności <math>k^{+}(L,k)\,</math> jest implikantem prostym, gdy <math>L\,</math> jest minimalnym pokryciem kolumnowym macierzy <math>B(k,R)\,</math>. | |||
|} | |} | ||
Wersja z 22:54, 28 sie 2006

|
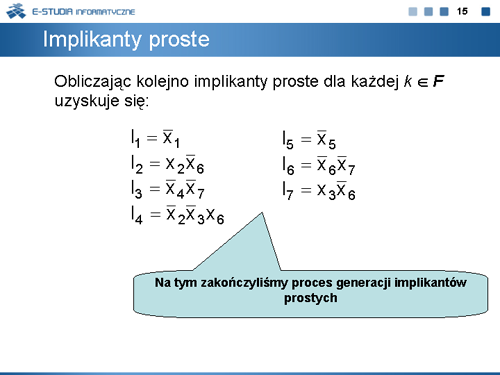
Minimalizacja funkcji boolowskich metodą ekspansji. |

|
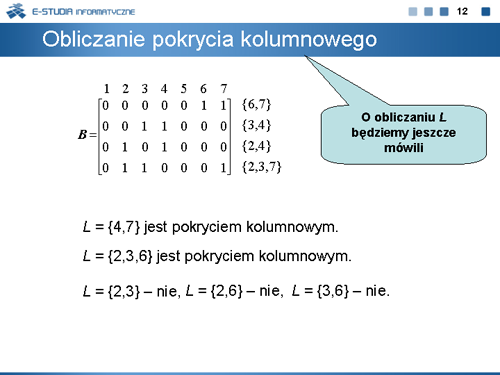
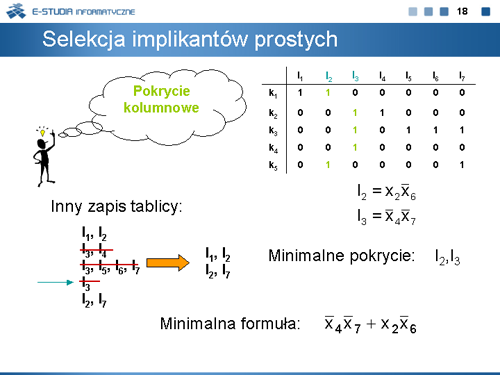
Pokryciem kolumnowym macierzy , , jest zbiór taki, że dla każdego istnieje , dla którego . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje , który jest pokryciem macierzy . |

|
|

|

|
|
|
|

|