PS Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 4: | Linia 4: | ||
*Przypominamy, że sygnały dyskretne o skończonej energii należą do przestrzeni Hilberta <math>l^2\,</math> , w której iloczyn skalarny jest określony wzorem <math>(x, y)_{l^2}=\sum_{-\infty}^{\infty} {x(nT_s)y^{*}(nT_s)}</math> . | *Przypominamy, że sygnały dyskretne o skończonej energii należą do przestrzeni Hilberta <math>l^2\,</math> , w której iloczyn skalarny jest określony wzorem <math>(x, y)_{l^2}=\sum_{-\infty}^{\infty} {x(nT_s)y^{*}(nT_s)}</math> . | ||
*Celowo przyjmujemy na razie nieunormowaną skalę czasu. | *Celowo przyjmujemy na razie nieunormowaną skalę czasu. | ||
*Podobnie jak w przypadku sygnałów analogowych widmo sygnału dyskretnego jest w ogólnym przypadku ciągłą funkcją zespoloną zmiennej rzeczywistej <math>\omega</math> . | *Podobnie jak w przypadku sygnałów analogowych widmo sygnału dyskretnego jest w ogólnym przypadku ciągłą funkcją zespoloną zmiennej rzeczywistej <math>\omega\,</math> . | ||
*W teorii sygnałów dyskretnych argument widma jest oznaczany zwyczajowo przez <math>e^{j\omega T_s}\,</math> , a nie w sposób naturalny przez <math>\omega</math> . | *W teorii sygnałów dyskretnych argument widma jest oznaczany zwyczajowo przez <math>e^{j\omega T_s}\,</math> , a nie w sposób naturalny przez <math>\omega\,</math> . | ||
|} | |} | ||
| Linia 14: | Linia 14: | ||
|width="500px" valign="top"|[[Grafika:PS_M4_Slajd2.png]] | |width="500px" valign="top"|[[Grafika:PS_M4_Slajd2.png]] | ||
|valign="top"| | |valign="top"| | ||
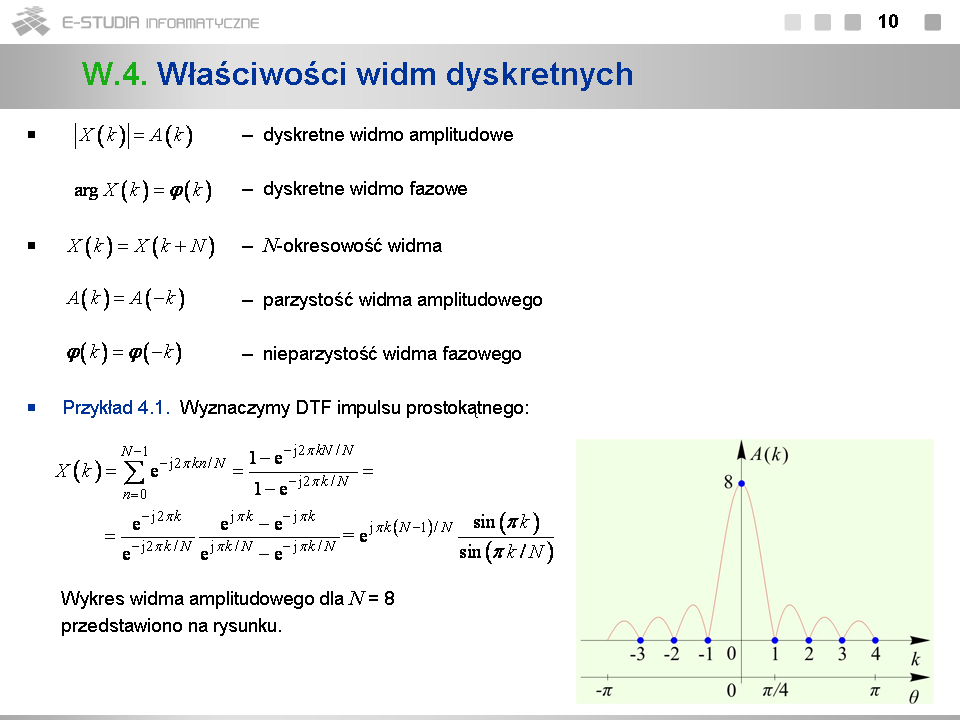
*Okresowość widm sygnałów dyskretnych jest ich podstawową cechą. Gdybyśmy widma te wyrazili w funkcji częstotliwości <math>f=\omega/2\pi</math> , ich okres byłby równy częstotliwości próbkowania <math>f_s\,</math> . | |||
*Jeśli widmo sygnału dyskretnego jest wyrażone w funkcji pulsacji unormowanej <math>\theta=\omega/2\pi</math> , jego okres jest równy <math>\pi\,</math> . | |||
*Widmo (4.2) można także zapisać w funkcji częstotliwości unormowanej <math>\nu=\omega/{\omega_s}=f/f_s=\theta/2\pi</math> . Jego okres jest wówczas równy <math>1\,</math>. | |||
|} | |} | ||
| Linia 22: | Linia 25: | ||
|width="500px" valign="top"|[[Grafika:PS_M4_Slajd3.png]] | |width="500px" valign="top"|[[Grafika:PS_M4_Slajd3.png]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo impulsu Kroneckera jest stałe przedziale <math>-\pi\le \theta \le \pi\,</math> , a zarazem na całej osi <math>\theta\,</math> . | |||
*Korzystanie ze wzorów na sumę skończonego lub nieskończonego szeregu geometrycznego jest charakterystyczne dla obliczania widm wielu sygnałów dyskretnych. | |||
|} | |} | ||
| Linia 30: | Linia 35: | ||
|width="500px" valign="top"|[[Grafika:PS_M4_Slajd4.png]] | |width="500px" valign="top"|[[Grafika:PS_M4_Slajd4.png]] | ||
|valign="top"| | |valign="top"| | ||
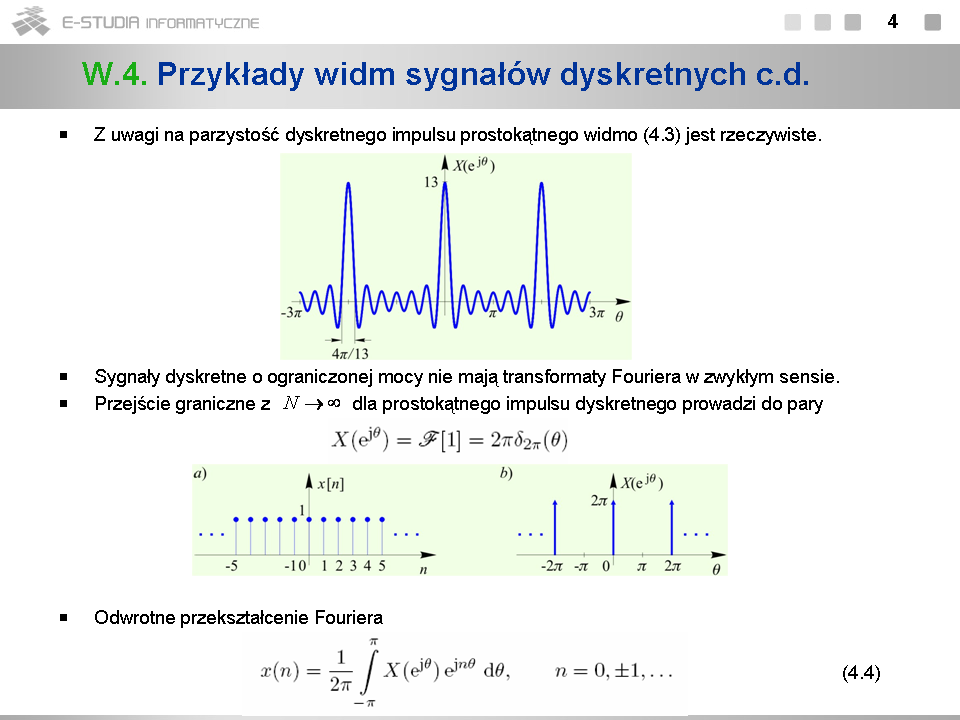
*Wykres widma amplitudowego dyskretnego impulsu prostokątnego został sporządzony dla <math>N=6\,</math> w przedziale <math>[-3\pi, 3\pi]\,</math> . Jeśli <math>N\,</math> rośnie, wysokość okresowo powtarzanych „listków” głównych widma rośnie, a ich szerokość maleje. Jednocześnie maleje poziom listków bocznych. | |||
*Zwiększając <math>N\,</math> do nieskończoności otrzymujemy w granicy dyskretny sygnał stały. Przejściu granicznemu towarzyszy wzrost wysokości listków głównych widma do nieskończoności i zanikanie listków bocznych do zera. W efekcie otrzymujemy dystrybucję grzebieniową w dziedzinie częstotliwości (rys. b) | |||
*Wzór (4.4) określa wartości kolejnych próbek sygnału dla <math>n \epsilon \Box\,</math> . | |||
|} | |} | ||
Wersja z 16:44, 25 sie 2006

|

|

|

|

|
|

|

|

|

|
|