|
|
| Linia 2: |
Linia 2: |
| |width="500px" valign="top"|[[Grafika:PS_M4_Slajd1.png]] | | |width="500px" valign="top"|[[Grafika:PS_M4_Slajd1.png]] |
| |valign="top"| | | |valign="top"| |
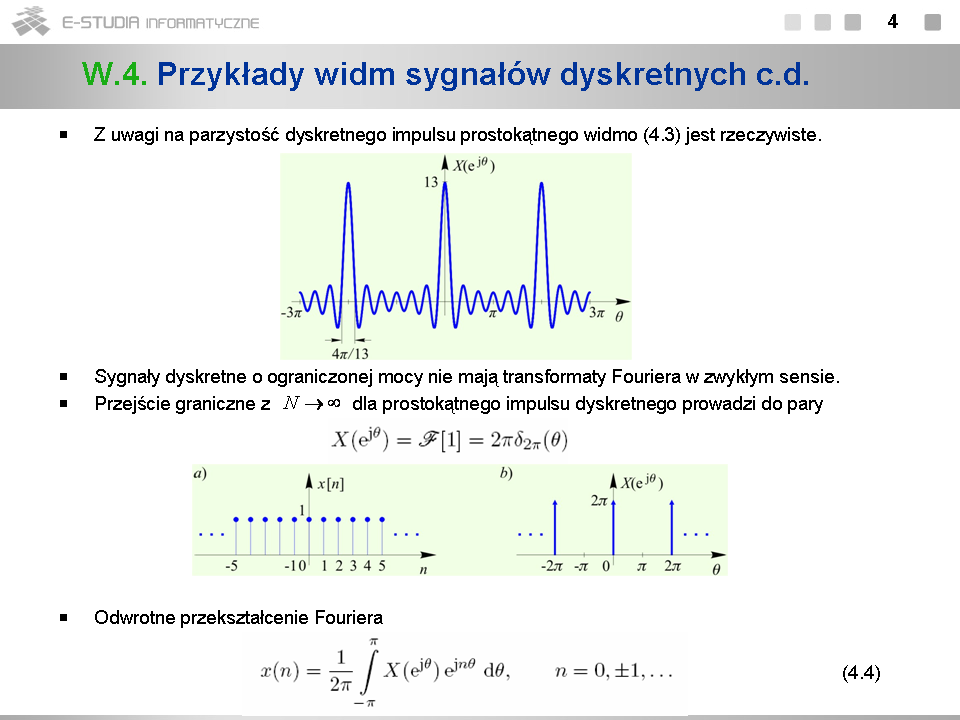
| | *Przypominamy, że sygnały dyskretne o skończonej energii należą do przestrzeni Hilberta <math>l^2\,</math> , w której iloczyn skalarny jest określony wzorem <math>(x, y)_{l^2}=\sum_{-\infty}^{\infty} {x(nT_s)y^{*}(nT_s)}</math> . |
| | *Celowo przyjmujemy na razie nieunormowaną skalę czasu. |
| | *Podobnie jak w przypadku sygnałów analogowych widmo sygnału dyskretnego jest w ogólnym przypadku ciągłą funkcją zespoloną zmiennej rzeczywistej <math>\omega</math> . |
| | *W teorii sygnałów dyskretnych argument widma jest oznaczany zwyczajowo przez <math>e^{j\omega T_s}\,</math> , a nie w sposób naturalny przez <math>\omega</math> . |
|
| |
|
| |} | | |} |