PS Moduł 3

Metody analizy sygnałów w dziedzinie częstotliwości noszą nazwę metod częstotliwościowych lub metod widmowych. W „języku” częstotliwościowym można w wielu przypadkach w sposób prostszy opisać podstawowe cechy sygnału. Łatwiej jest też rozpatrywać i interpretować niektóre operacje na sygnałach, a zwłaszcza operację filtracji. Widmo $X(\omega )$ sygnału $x(t)$ jest jego równoważną reprezentacją w dziedzinie częstotliwości. Ponieważ widmo jest w ogólnym przypadku funkcją zespoloną zmiennej rzeczywistej $\omega$ (por. przykład 3.1), reprezentacja ta ma charakter formalny, niefizyczny.

---

Zwróćmy uwagę, że w przykładzie 3.2 otrzymaliśmy widmo rzeczywiste. Jest to konsekwencją parzystości sygnału $x(t)=X_0\mathrm{\Pi }(t/T)$ . Widmo to ma kształt funkcji Sa w dziedzinie częstotliwości. Dla sygnałów o ograniczonej energii (należących do przestrzeni $L^2(-\mathrm{\infty },\mathrm{\infty })$ ) przekształcenie Fouriera jest wzajemnie jednoznaczne, jeśli całkę (3.1) rozumie się w sensie Lebesgue’a. Wzory (3.1) i (3.2) określają proste i odwrotne przekształcenie Fouriera w sensie zwykłym.

---

Chcąc wyprowadzić parę transformat w sensie granicznym należy w każdym indywidualnym przypadku skonstruować odpowiedni ciąg sygnałów o ograniczonej energii aproksymujący sygnał o ograniczonej mocy i dokonać przejścia granicznego. Bardzo często w wyniku przejścia granicznego otrzymujemy w granicy widma dystrybucyjne. Ciąg aproksymujący sygnał $x(t)$ o ograniczonej mocy konstruuje się zwykle mnożąc go przez funkcje dążące dostatecznie szybko do zera dla $t\to \pm \mathrm{\infty }$ typu: $e^{-\alpha t}1(t)$ , jeśli $tϵ[0,\mathrm{\infty })$ , oraz Parser nie mógł rozpoznać (błąd składni): {\displaystyle e^{-\alpha |t|}\} lub Parser nie mógł rozpoznać (błąd składni): {\displaystyle e^{-\alpha t^2}\} , jeśli $tϵ(-\mathrm{\infty },\mathrm{\infty })$ .

---

Widmo amplitudowe i widmo fazowe są funkcjami rzeczywistymi zmiennej $\omega$ i mają wyraźną interpretację fizyczną. Widma amplitudowe sygnału z przykładu 3.3 dąży do zera, gdy $\omega \to \pm \mathrm{\infty }$ . Jego gęstość widmowa jest skoncentrowana głównie w zakresie małych wartości pulsacji. Sygnały takie nazywamy dolnopasmowymi.

---

Widmo amplitudowe impulsu prostokątnego z przykładu 3.4 ma charakterystyczną strukturę „listkową”. Środkowy przedział pulsacji $|\omega |<2\pi /T$ obejmuje tzw. listek główny, a po obu jego stronach występują listki boczne. Impuls prostokątny jest również sygnałem dolnopasmowym.

---

Widmo amplitudowe sygnałów rzeczywistych jest funkcją parzystą, a widmo fazowe funkcją nieparzystą zmiennej $\omega$ . Widmo tych sygnałów jest zatem funkcją hermitowską, tj. $X(\omega )=X^{*}(-\omega )$ . Operacje zwierciadlanego odbicia sygnału względem osi rzędnych i jego sprzężenia odpowiadają podobnym operacjom na jego widmie. Przekształcenie Fouriera jest liniowe, tzn. widmo kombinacji liniowej sygnałów jest taką samą kombinacją liniową ich widm. Przy przekształceniu Fouriera kształt sygnału i jego widma jest cechą wymienną. Rozciągnięciu skali czasu sygnału odpowiada zawężenie skali częstotliwości jego widma i odwrotnie. Jednocześnie zmianie ulega skala wartości widma. Przesunięciu sygnału wzdłuż osi czasu o czas $t_0$ odpowiada mnożenie jego widma przez czynnik $e^{j\omega t_0}$ . Widmo amplitudowe nie zmienia się przy tym, a fazowe ulega zmianie o składnik $-\omega t_0$ . Mnożenie sygnału przez zespolony sygnał harmoniczny o pulsacji ${\omega }_0$ powoduje przesunięcie jego widma wzdłuż osi pulsacji o wartość ${\omega }_0$ . Mnożenie sygnału przez rzeczywisty sygnał harmoniczny o pulsacji ${\omega }_0$ (jego modulacja) powoduje rozczepienie widma na dwie części przesunięte wzdłuż osi pulsacji do punktów $\pm {\omega }_0$ . Jednocześnie gęstość widmowa maleje dwukrotnie

---

Różniczkowaniu sygnału w dziedzinie czasu odpowiada mnożenie jego widma przez $j\omega$ w dziedzinie częstotliwości. Całkowaniu sygnału w dziedzinie czasu odpowiada dzielenie jego widma przez $j\omega$ w dziedzinie częstotliwości. Splotowi sygnałów odpowiada mnożenie ich widm i odwrotnie, mnożeniu sygnałów odpowiada splatanie ich widm. Twierdzenie Rayleigha orzeka, że (z dokładnością do czynnika $2\pi$ ) w przestrzeniach sygnałów ${L^2}_t$ i widm ${L^2}_{\omega }$ jest zachowany iloczyn skalarny. Wynikające z niego twierdzenie Parsevala orzeka, że z dokładnością do czynnika $2\pi$ zachowana jest norma w obu przestrzeniach (lub równoważnie energia). Widmo gęstości energii opisuje rozkład całkowitej energii sygnału wzdłuż osi pulsacji.

---

Ponieważ sygnał wykładniczy obustronny jest parzysty jego widmo jest rzeczywiste i parzyste. Jak widać, jest to sygnał dolnopasmowy. Parę tę można bez trudu wyprowadzić wprost z definicji przekształcenia Fouriera. Obliczenie widma sygnału $Sa$ wprost z definicji jest bardzo złożone. Korzystając natomiast z twierdzenia o symetrii względem wcześniej wyprowadzonej pary transformat dla impulsu prostokątnego, widmo to można wyznaczyć bez trudu. Ponieważ widmo sygnału Sa jest prostokątne, sygnał ten nazywamy idealnym sygnałem dolnopasmowym. Widmo impulsu trójkątnego można wyznaczyć z twierdzenia o splocie w dziedzinie czasu przyjmując $x(t)=y(t)=\mathrm{\Pi }(t/T)$ . Widmo sygnału $S{a}^2$ wynika z twierdzenia o symetrii i ostatniej pary transformat.

---

Widmo sygnału Gaussa ma również kształt krzywej Gaussa. Jest to jedna z nielicznych par transformat Fouriera o tej właściwości Widmo prostokątnego impulsu radiowego można wyznaczyć z twierdzenia o modulacji zastosowanego do widma impulsu prostokątnego.

---

Widmo impulsu Diraca jest stałe w całym przedziale pulsacji. Widmo takie nazywamy białym. Widmo sygnału stałego jest dystrybucją Diraca w dziedzinie częstotliwości o polu $2\pi$ w punkcie $\omega =0$ . Sygnał $sgnt$ jest nieparzysty, dlatego jego widmo jest urojone. Para $1/\pi t\leftrightarrow -jsgn\omega$ jest dualna względem pary $sgnt\leftrightarrow 2/j\omega$ i wynika z twierdzenia o symetrii.

---

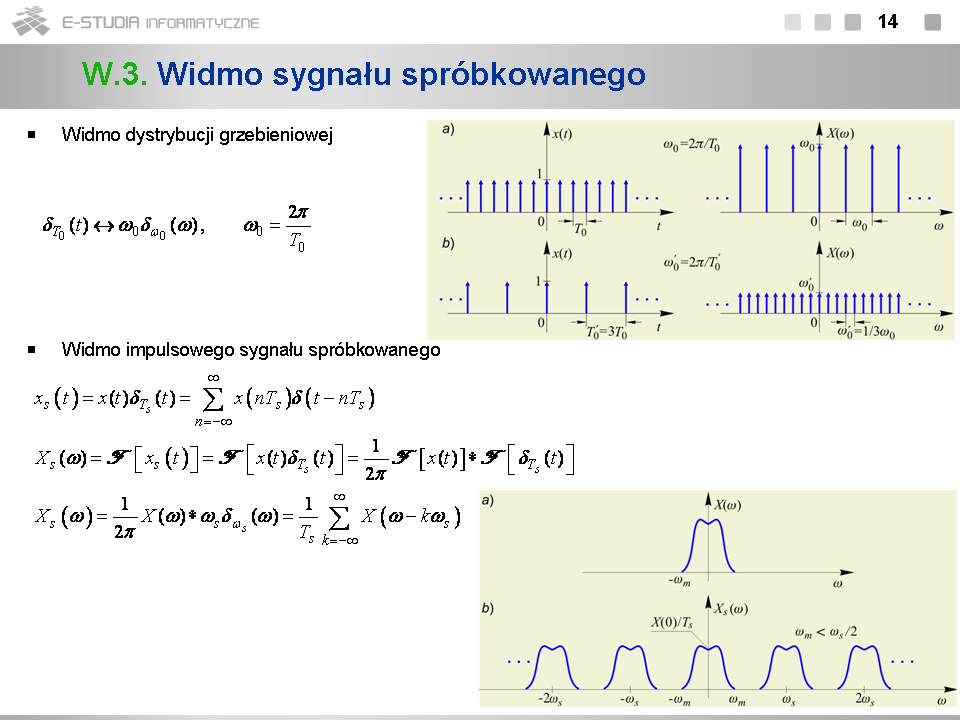
Widmo skoku jednostkowego można wyznaczyć, przedstawiając go w postaci $1(t)=1/2+(sgnt)/2$ i korzystając z poprzednio omówionych par. Widmo sygnału harmonicznego wynika z twierdzenia o modulacji zastosowanego do pary $1\leftrightarrow 2\pi \delta (\omega )$ . Widmo to składa się z dwóch dystrybucji Diraca (prążków) występujących w punktach $\pm {\omega }_0$ . Widmo zespolonego sygnału harmonicznego o pulsacji ${\omega }_0$ jest dystrybucją Diraca w punkcie ${\omega }_0$ o polu $2\pi$ .

---

---

---

---

---

---

</math>