PS Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 33: | Linia 33: | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd4.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd4.png]] | ||
|valign="top"| | |valign="top"| | ||
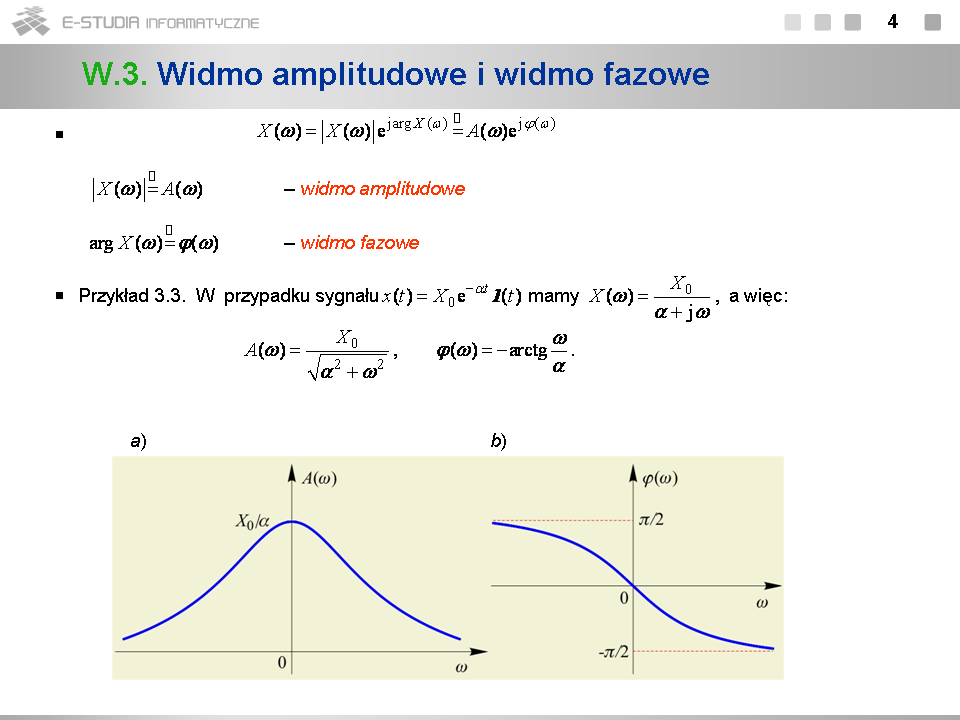
*Widmo amplitudowe i widmo fazowe są funkcjami rzeczywistymi zmiennej <math>\omega\,</math> i mają wyraźną interpretację fizyczną. | |||
*Widma amplitudowe sygnału z przykładu 3.3 dąży do zera, gdy <math>\omega\to \pm \infty\,</math> . Jego gęstość widmowa jest skoncentrowana głównie w zakresie małych wartości pulsacji. Sygnały takie nazywamy ''dolnopasmowymi''. | |||
|} | |} | ||
| Linia 41: | Linia 43: | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd5.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd5.png]] | ||
|valign="top"| | |valign="top"| | ||
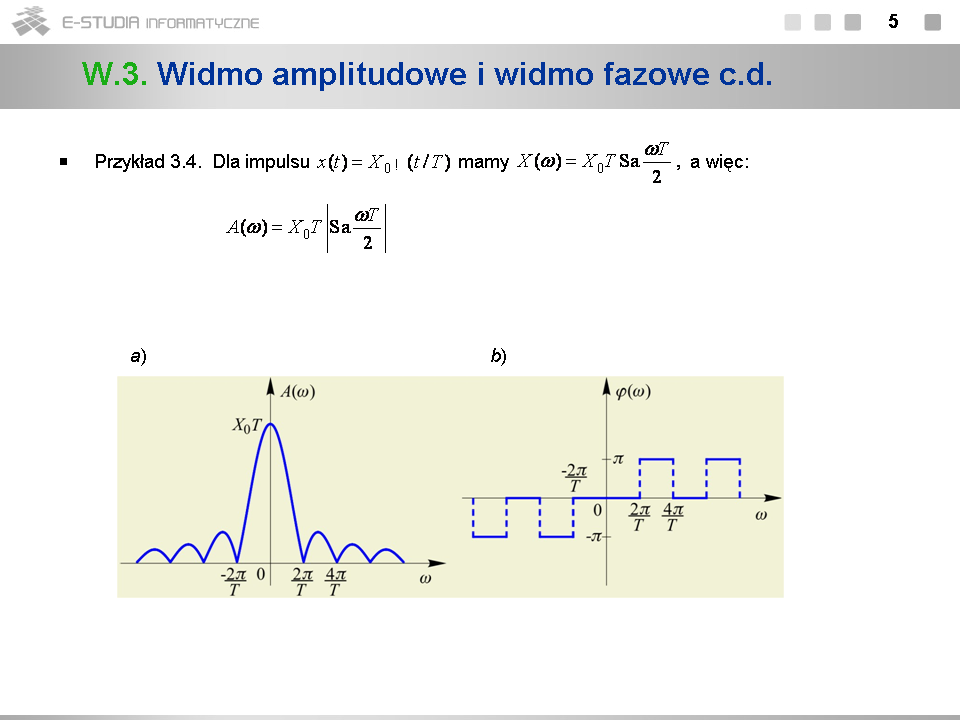
*Widmo amplitudowe impulsu prostokątnego z przykładu 3.4 ma charakterystyczną strukturę „listkową”. Środkowy przedział pulsacji <math>|\omega|<2\pi /T</math> obejmuje tzw. ''listek główny'', a po obu jego stronach występują ''listki boczne''. | |||
*Impuls prostokątny jest również sygnałem dolnopasmowym. | |||
|} | |} | ||
| Linia 49: | Linia 53: | ||
|width="500px" valign="top"|[[Grafika:PS_M3_Slajd6.png]] | |width="500px" valign="top"|[[Grafika:PS_M3_Slajd6.png]] | ||
|valign="top"| | |valign="top"| | ||
*Widmo amplitudowe sygnałów rzeczywistych jest funkcją parzystą, a widmo fazowe funkcją nieparzystą zmiennej <math>\omega\,</math> . Widmo tych sygnałów jest zatem ''funkcją hermitowską'', tj. <math>X(\omega)=X^{*}(-\omega)</math> . | |||
*Operacje zwierciadlanego odbicia sygnału względem osi rzędnych i jego sprzężenia odpowiadają podobnym operacjom na jego widmie. | |||
*Przekształcenie Fouriera jest liniowe, tzn. widmo kombinacji liniowej sygnałów jest taką samą kombinacją liniową ich widm. | |||
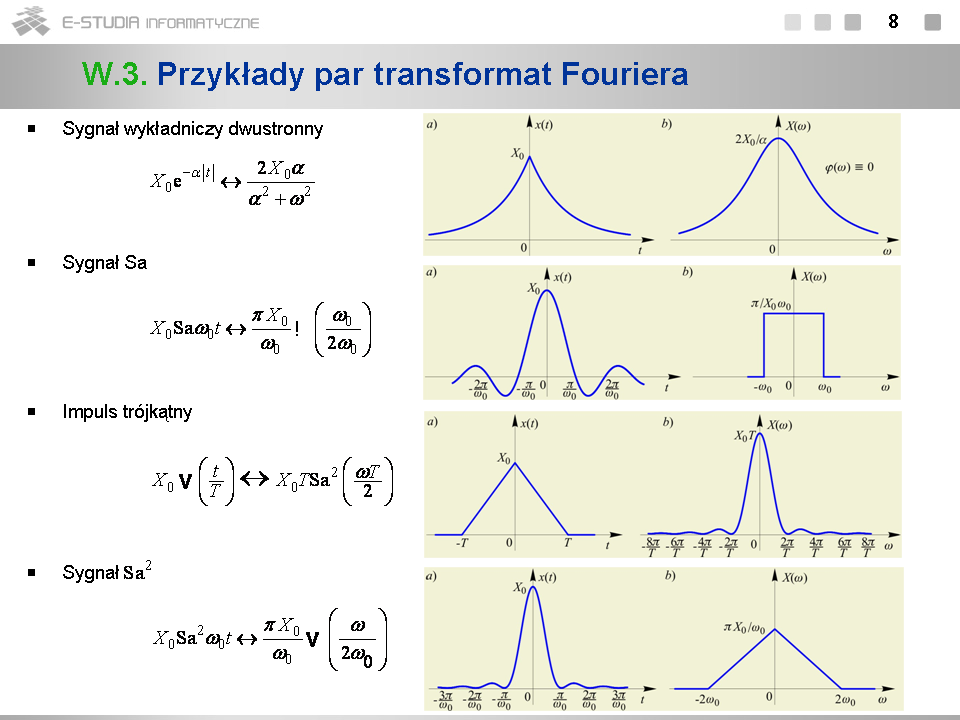
*Przy przekształceniu Fouriera kształt sygnału i jego widma jest cechą wymienną. | |||
*Rozciągnięciu skali czasu sygnału odpowiada zawężenie skali częstotliwości jego widma i odwrotnie. Jednocześnie zmianie ulega skala wartości widma. | |||
*Przesunięciu sygnału wzdłuż osi czasu o czas <math>t_0\,</math> odpowiada mnożenie jego widma przez czynnik <math>e^{j\omega t_0}\,</math> . Widmo amplitudowe nie zmienia się przy tym, a fazowe ulega zmianie o składnik <math>-\omega t_0\,</math> . | |||
*Mnożenie sygnału przez zespolony sygnał harmoniczny o pulsacji <math>\omega_0\,</math> powoduje przesunięcie jego widma wzdłuż osi pulsacji o wartość <math>\omega_0\,</math> . | |||
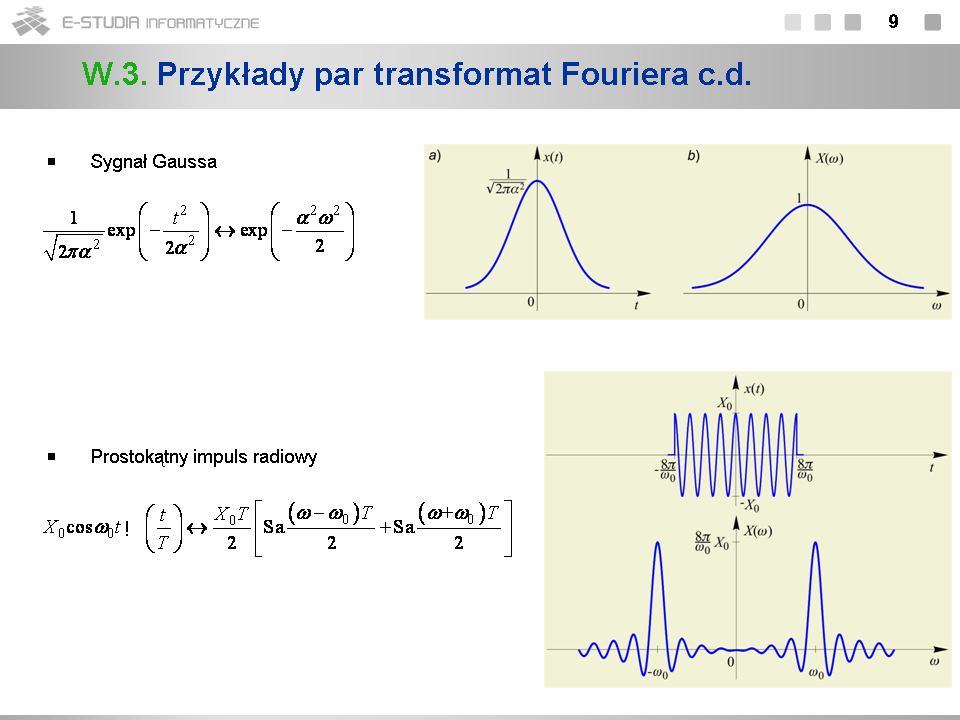
*Mnożenie sygnału przez rzeczywisty sygnał harmoniczny o pulsacji <math>\omega_0\,</math> (jego modulacja) powoduje rozczepienie widma na dwie części przesunięte wzdłuż osi pulsacji do punktów <math>\pm \omega_0\,</math> . Jednocześnie gęstość widmowa maleje dwukrotnie | |||
|} | |} | ||
Wersja z 15:26, 25 sie 2006

|
|
|
|
|

|

|
|

|
|
</math>