PS Moduł 3

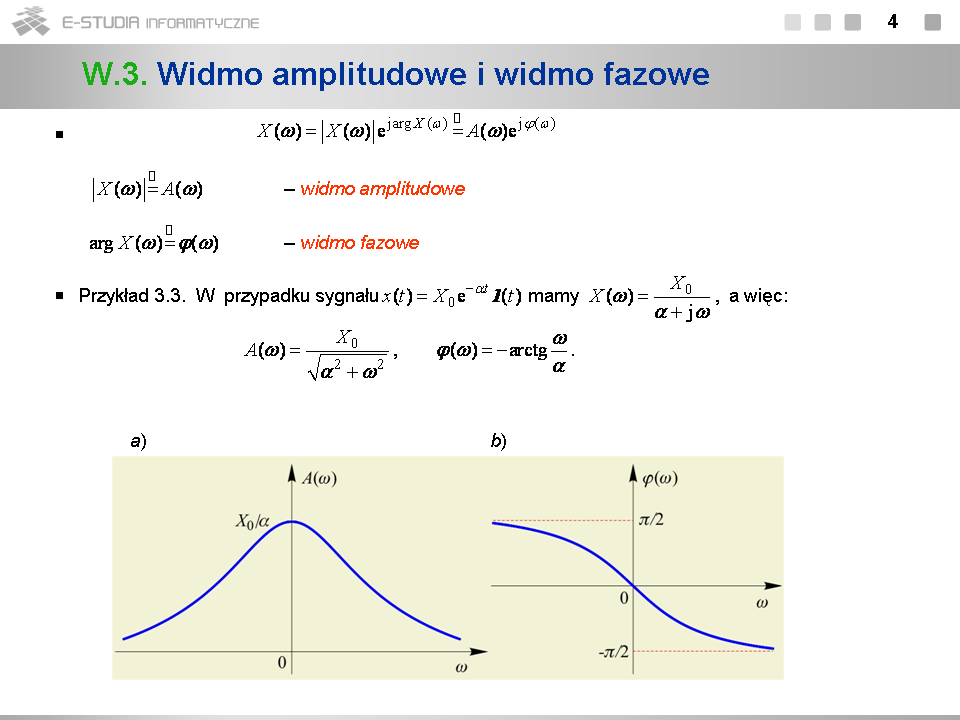
Metody analizy sygnałów w dziedzinie częstotliwości noszą nazwę metod częstotliwościowych lub metod widmowych. W „języku” częstotliwościowym można w wielu przypadkach w sposób prostszy opisać podstawowe cechy sygnału. Łatwiej jest też rozpatrywać i interpretować niektóre operacje na sygnałach, a zwłaszcza operację filtracji. Widmo $X(\omega )$ sygnału $x(t)$ jest jego równoważną reprezentacją w dziedzinie częstotliwości. Ponieważ widmo jest w ogólnym przypadku funkcją zespoloną zmiennej rzeczywistej $\omega$ (por. przykład 3.1), reprezentacja ta ma charakter formalny, niefizyczny.

---

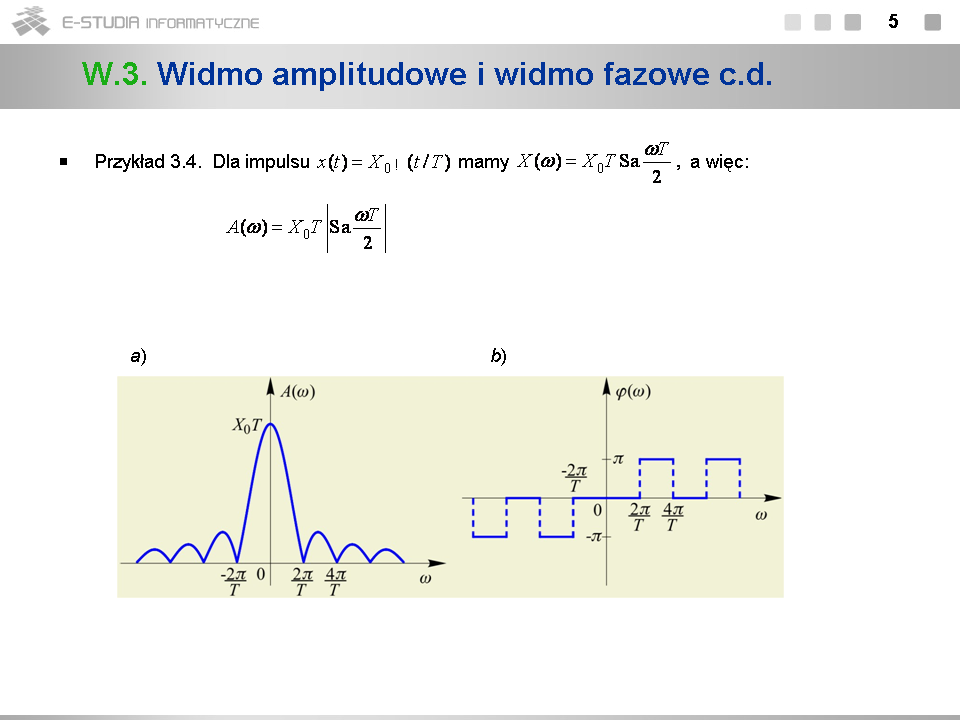
Zwróćmy uwagę, że w przykładzie 3.2 otrzymaliśmy widmo rzeczywiste. Jest to konsekwencją parzystości sygnału $x(t)=X_0\mathrm{\Pi }(t/T)$ . Widmo to ma kształt funkcji Sa w dziedzinie częstotliwości. Dla sygnałów o ograniczonej energii (należących do przestrzeni $L^2(-\mathrm{\infty },\mathrm{\infty })$ ) przekształcenie Fouriera jest wzajemnie jednoznaczne, jeśli całkę (3.1) rozumie się w sensie Lebesgue’a. Wzory (3.1) i (3.2) określają proste i odwrotne przekształcenie Fouriera w sensie zwykłym.

---

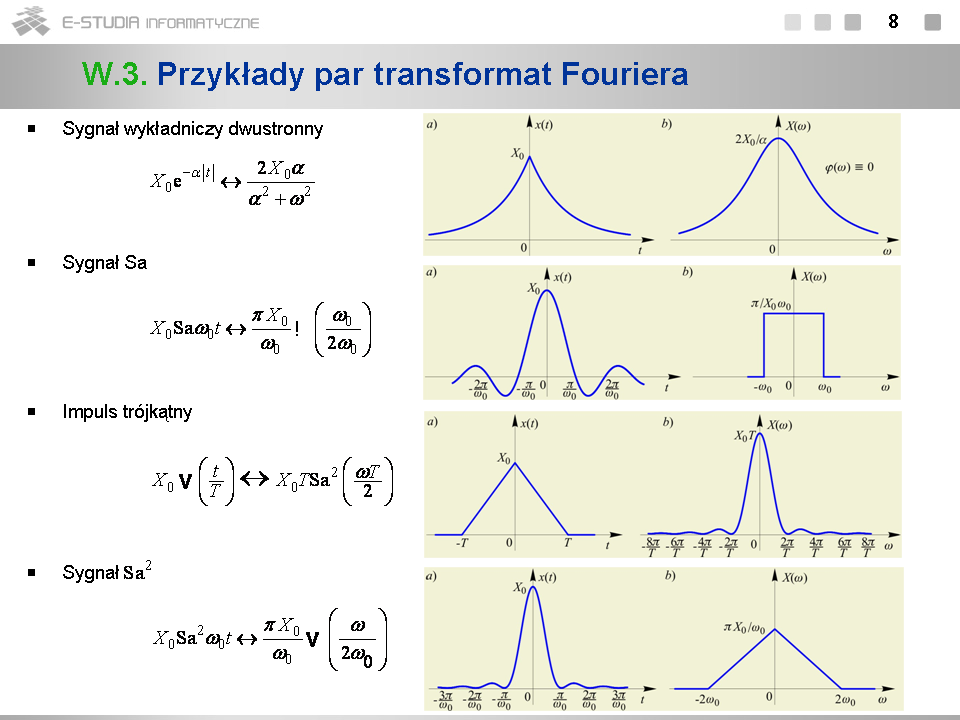
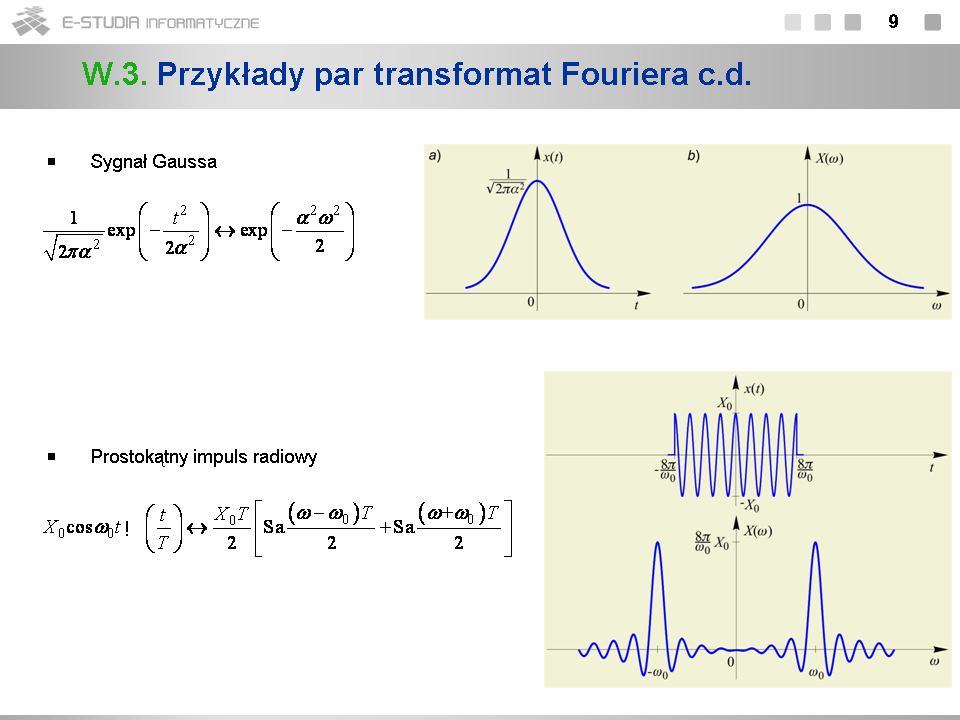
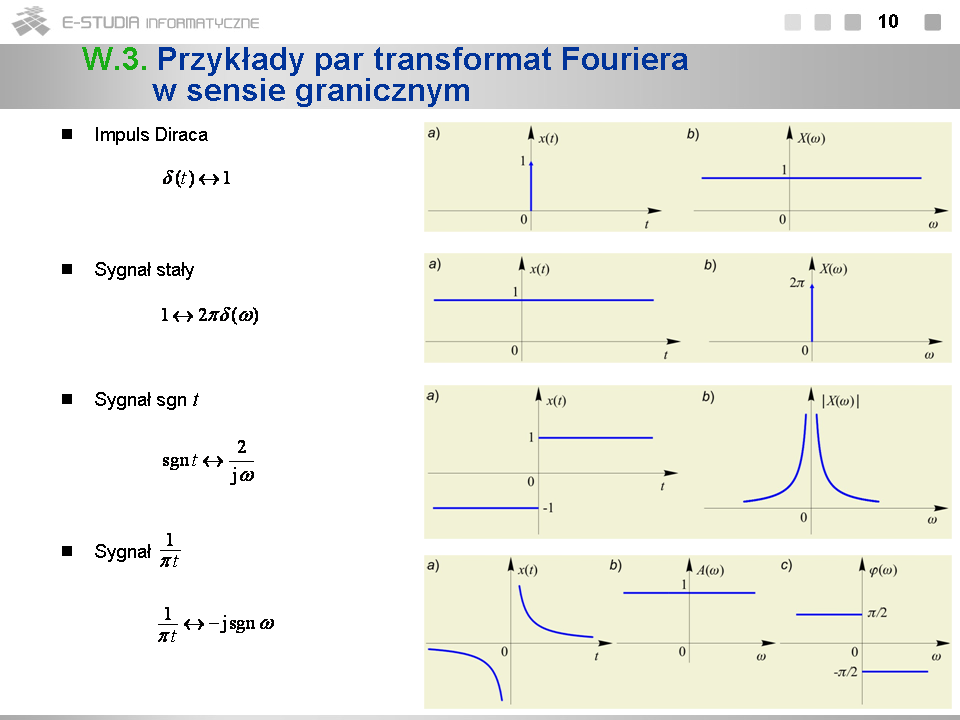
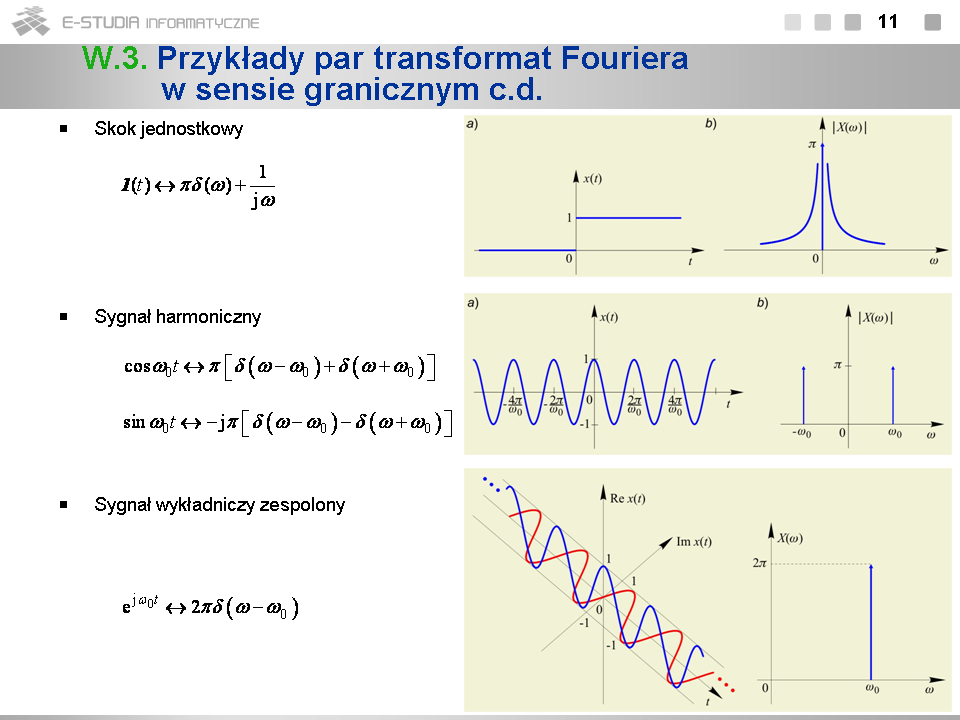
Chcąc wyprowadzić parę transformat w sensie granicznym należy w każdym indywidualnym przypadku skonstruować odpowiedni ciąg sygnałów o ograniczonej energii aproksymujący sygnał o ograniczonej mocy i dokonać przejścia granicznego. Bardzo często w wyniku przejścia granicznego otrzymujemy w granicy widma dystrybucyjne. Ciąg aproksymujący sygnał $x(t)$ o ograniczonej mocy konstruuje się zwykle mnożąc go przez funkcje dążące dostatecznie szybko do zera dla $t\to \pm \mathrm{\infty }$ typu: $e^{-\alpha t}1(t)$ , jeśli $tϵ[0,\mathrm{\infty })$ , oraz Parser nie mógł rozpoznać (błąd składni): {\displaystyle e^{-\alpha |t|}\} lub Parser nie mógł rozpoznać (błąd składni): {\displaystyle e^{-\alpha t^2}\} , jeśli $tϵ(-\mathrm{\infty },\mathrm{\infty })$ .

---

---

---

---

---

---

---

---

---

---

---

---

---

---

</math>