PS Moduł 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 202: | Linia 202: | ||
|width="500px" valign="top"|[[Grafika:PS_M2_Slajd19.png]] | |width="500px" valign="top"|[[Grafika:PS_M2_Slajd19.png]] | ||
|valign="top"| | |valign="top"| | ||
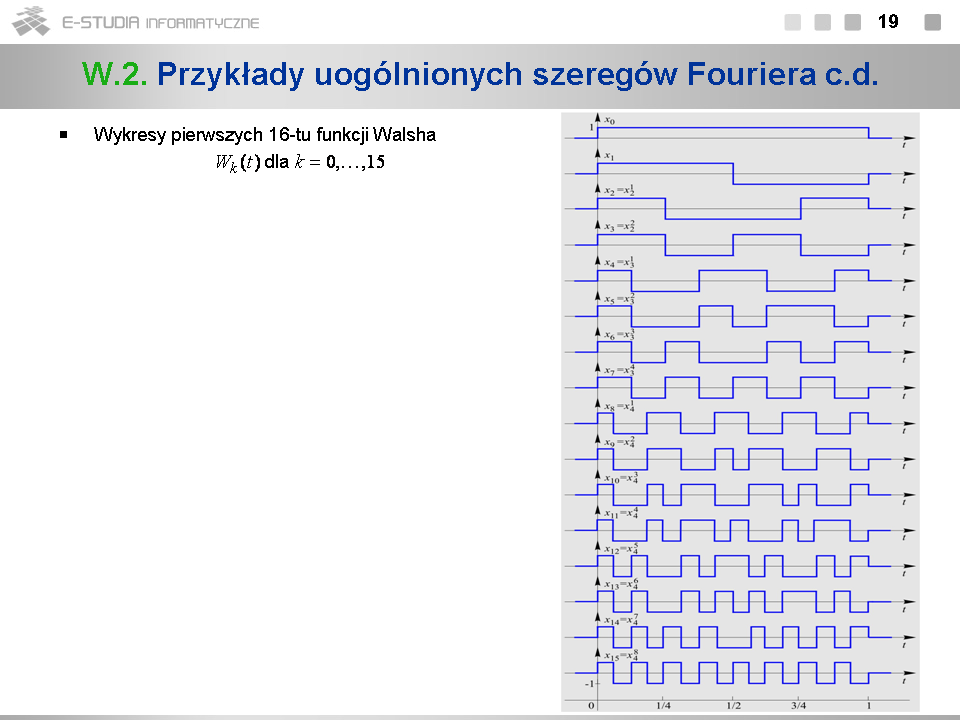
*Podobnie jak funkcje Haara funkcje Walsha można uporządkować według jednego wskaźnika <math>k\,</math> , definiując: <math>W_0(t)=x_0(t)</math> , <math>W_1(t)=x_1(t)</math> , <math>W_k(t)={x^i}_m(t)</math> dla <math>k=2,3,...\,</math> , gdzie <math>k=2^{m-1}+i-1\,</math> oraz <math> | *Podobnie jak funkcje Haara funkcje Walsha można uporządkować według jednego wskaźnika <math>k\,</math> , definiując: <math>W_0(t)=x_0(t)</math> , <math>W_1(t)=x_1(t)</math> , <math>W_k(t)={x^i}_m(t)</math> dla <math>k=2,3,...\,</math> , gdzie <math>k=2^{m-1}+i-1\,</math> oraz <math>i=1,...,2^{m-1}\,</math> . | ||
*Przy takiej numeracji numer <math>k\,</math> funkcji Walsha <math>W_k(t)\,</math> jest równy liczbie jej przejść przez zero. | *Przy takiej numeracji numer <math>k\,</math> funkcji Walsha <math>W_k(t)\,</math> jest równy liczbie jej przejść przez zero. | ||
*Funkcje o numerach <math>2^k-1\,</math> , <math>k=1,2,...\,</math> są odcinkami zwykłych okresowych bipolarnych fal prostokątnych. | *Funkcje o numerach <math>2^k-1\,</math> , <math>k=1,2,...\,</math> są odcinkami zwykłych okresowych bipolarnych fal prostokątnych. | ||
Wersja z 14:17, 25 sie 2006

|
|

|
|