PS Moduł 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 202: | Linia 202: | ||
|width="500px" valign="top"|[[Grafika:PS_M2_Slajd19.png]] | |width="500px" valign="top"|[[Grafika:PS_M2_Slajd19.png]] | ||
|valign="top"| | |valign="top"| | ||
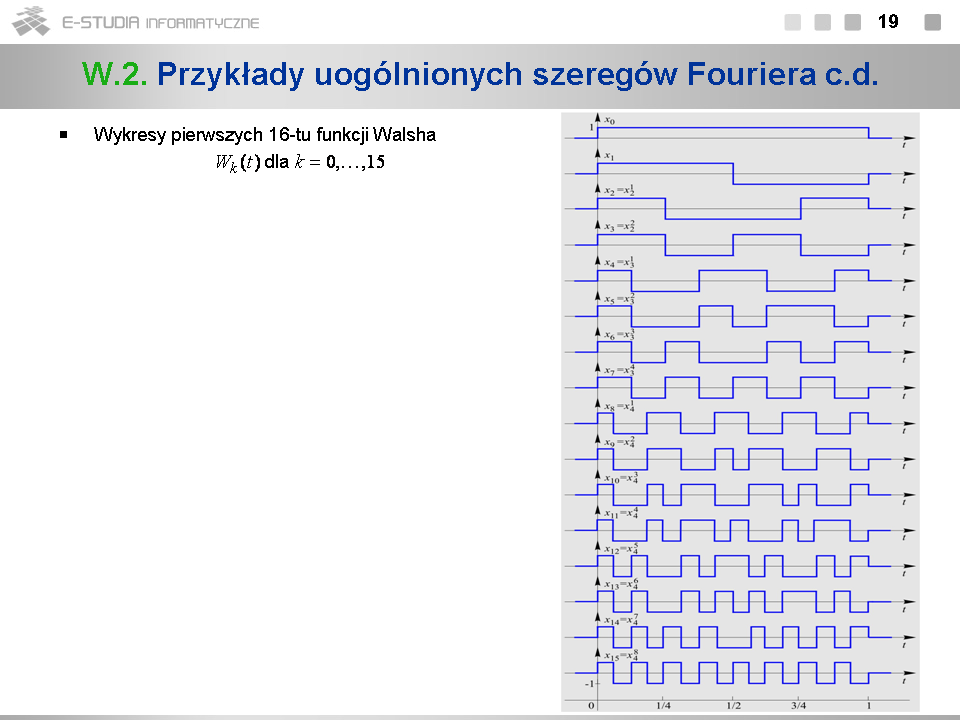
*Podobnie jak funkcje Haara funkcje Walsha można uporządkować według jednego wskaźnika | *Podobnie jak funkcje Haara funkcje Walsha można uporządkować według jednego wskaźnika <math>k\,</math> , definiując: <math>W_0(t)=x_0(t)</math> , <math>W_1(t)=x_1(t)</math> , <math>W_k(t)={x^i}_m(t)</math> dla <math>k=2,3,...\,</math> , gdzie <math>k=2^{m-1}+i-1\,</math> oraz <math>l=1,...,2^{m-1}\,</math> . | ||
*Przy takiej numeracji numer <math>k\,</math> funkcji Walsha <math>W_k(t)\,</math> jest równy liczbie jej przejść przez zero. | |||
*Funkcje o numerach <math>2^k-1\,</math> , <math>k=1,2,...\,</math> są odcinkami zwykłych okresowych bipolarnych fal prostokątnych. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M2_Slajd20.png]] | |||
|valign="top"| | |||
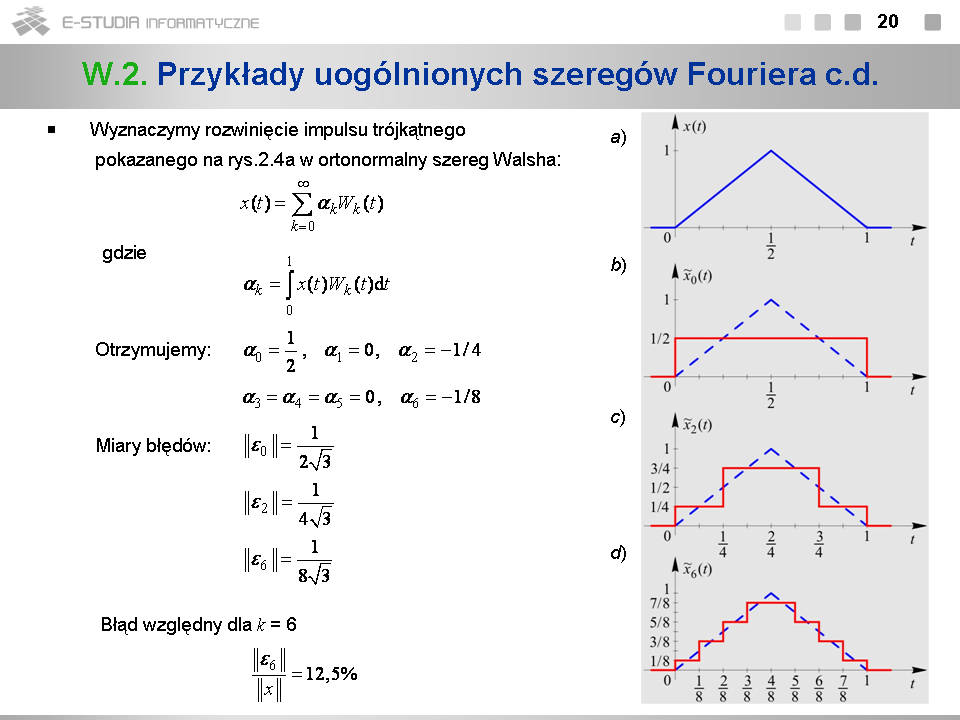
*Widzimy, że w miarę zwiększania liczby znaczących wyrazów szeregu Walsha sygnał aproksymujący coraz bardziej zbliża się kształtem do impulsu trójkątnego. Dodanie następnych wyrazów niezerowych jeszcze bardziej zwiększy dokładność aproksymacji. | |||
*Gdyby jako miarę błędu przyjąć nie normę sygnału błędu, lecz jego energię (kwadrat normy), błąd względny aproksymacji dla <math>k=6\,</math> wyniósłby <math>1,56\%\,</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M2_Slajd21.png]] | |||
|valign="top"| | |||
*Rozwinięcie sygnału <math>x(t)\epsilon {L^2}_{T_0}</math> w trygonometryczny rzeczywisty lub zespolony szereg Fouriera względem baz ortogonalnych prowadzi do nieco prostszych zapisów tych szeregów, niż w przypadku ich rozwijania względem baz ortonormalnych. Dlatego z reguły korzysta się z tych drugich postaci szeregów Fouriera. Podkreślmy, że postacie te (przy oznaczeniu <math>\omega_0=2\pi/T_0</math> ) były już cytowane na wykładzie 1 przy okazji omawiania przykładów różnych rodzajów reprezentacji sygnałów. | |||
*Miedzy współczynnikami rzeczywistego i zespolonego szeregu Fouriera zachodzą związki: | |||
:<math>X_0=a_0</math> , <math>X_k=\frac{a_k+jb_k}{2}</math> | |||
:oraz związki odwrotne: | |||
<math>a_0=X_0</math> , <math>a_k=X_k+X_{-k}</math> , <math>b_k=j(X_k-X_{-k})</math> | |||
:Umożliwiają one przejście z jednej postaci szeregu na drugą. | |||
Wersja z 14:04, 25 sie 2006

|
|

|
|