PS Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 17: | Linia 17: | ||
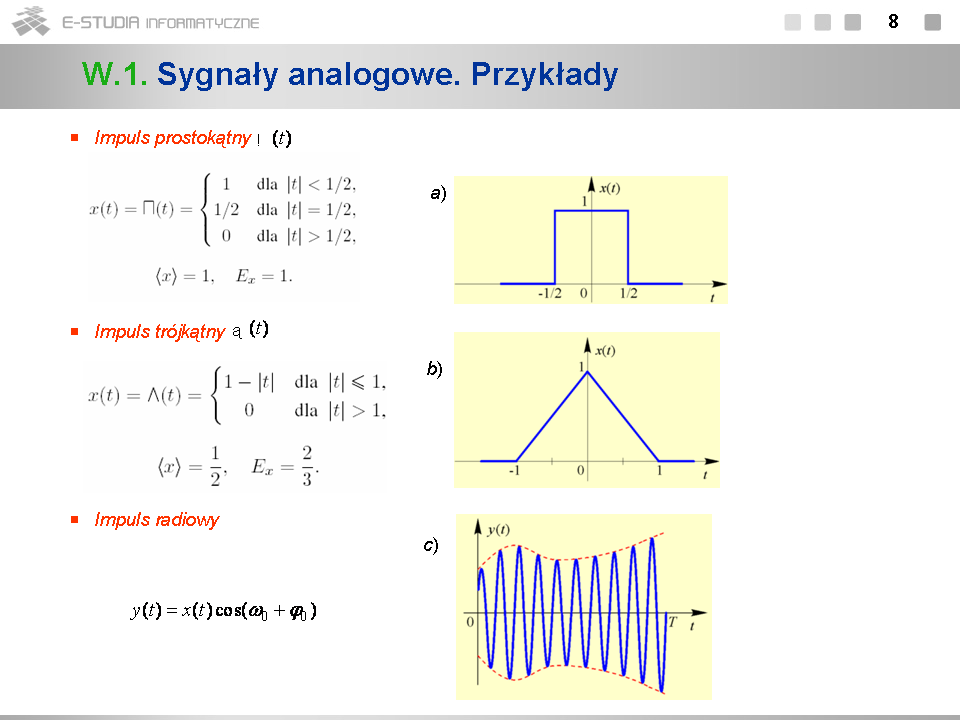
*Rozważania ograniczymy wyłącznie do ''sygnałów deterministycznych''. Omówienie sygnałów losowych wymaga znajomości teorii procesów stochastycznych. | *Rozważania ograniczymy wyłącznie do ''sygnałów deterministycznych''. Omówienie sygnałów losowych wymaga znajomości teorii procesów stochastycznych. | ||
*Sygnały dzielimy także ze względu na ich przeciwdziedzinę (zbiór wartości). Jeżeli zbiór ten jest ciągły, sygnał nazywamy ''ciągłym w amplitudzie''. Jeżeli jest on dyskretny (w szczególności skończony) sygnał nazywamy ''dyskretnym w amplitudzie''. | *Sygnały dzielimy także ze względu na ich przeciwdziedzinę (zbiór wartości). Jeżeli zbiór ten jest ciągły, sygnał nazywamy ''ciągłym w amplitudzie''. Jeżeli jest on dyskretny (w szczególności skończony) sygnał nazywamy ''dyskretnym w amplitudzie''. | ||
*Łącząc kryteria podziału sygnałów ze względu na rodzaj ich dziedziny i przeciwdziedziny, można wyodrębnić cztery klasy sygnałów: | *Łącząc kryteria podziału sygnałów ze względu na rodzaj ich dziedziny i przeciwdziedziny, można wyodrębnić cztery klasy sygnałów: | ||
**''z czasem ciągłym i ciągłe w amplitudzie'' | **''z czasem ciągłym i ciągłe w amplitudzie'' | ||
| Linia 186: | Linia 188: | ||
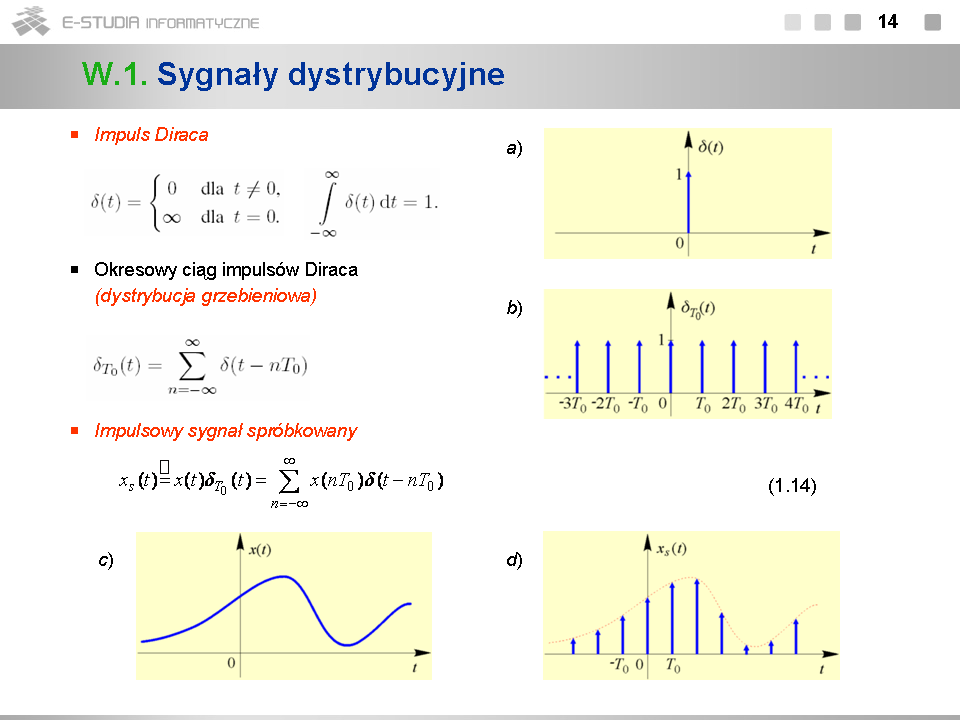
*Całka impulsu Diraca w granicach od <math>-\infty\,</math> do <math>t\,</math> jest równa sygnałowi skoku jednostkowego. Pochodna skoku jednostkowego jest równa impulsowi Diraca. Związki te należy jednak rozumieć w sensie dystrybucyjnym. | *Całka impulsu Diraca w granicach od <math>-\infty\,</math> do <math>t\,</math> jest równa sygnałowi skoku jednostkowego. Pochodna skoku jednostkowego jest równa impulsowi Diraca. Związki te należy jednak rozumieć w sensie dystrybucyjnym. | ||
*Splot sygnału <math>x(t)\,</math> z impulsem Diraca <math>\delta(t)\,</math> daje w wyniku ponownie sygnał <math>x(t)\,</math> . Oznacza to, że <math>\delta(t)\,</math> jest elementem identycznościowym operacji splotu. Splot sygnału <math>x(t)\,</math> z impulsem Diraca przesuniętym o czas <math>t_0\,</math> daje w wyniku niezmienioną kopię tego sygnału przesuniętą o ten sam czas. | *Splot sygnału <math>x(t)\,</math> z impulsem Diraca <math>\delta(t)\,</math> daje w wyniku ponownie sygnał <math>x(t)\,</math> . Oznacza to, że <math>\delta(t)\,</math> jest elementem identycznościowym operacji splotu. Splot sygnału <math>x(t)\,</math> z impulsem Diraca przesuniętym o czas <math>t_0\,</math> daje w wyniku niezmienioną kopię tego sygnału przesuniętą o ten sam czas. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd16.png]] | |||
|valign="top"| | |||
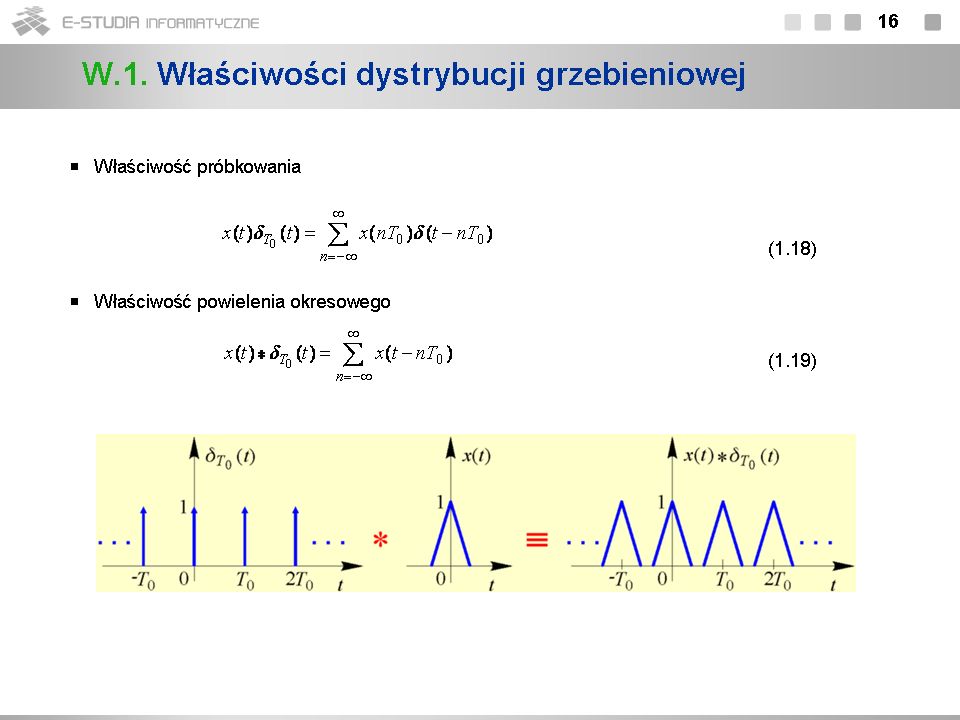
*Właściwość (1.18) jest uogólnieniem właściwości (1.15). Mnożenie sygnału <math>x(t)\,</math> przez ''dystrybucję grzebieniową'' daje w wyniku reprezentację dystrybucyjną sygnału sprókowanego w postaci impulsowego sygnału sprókowanego (1.14). | |||
*Zgodnie z właściwością (1.19), w wyniku splecenia sygnału <math>x(t)\,</math> z dystrybucją grzebieniową <math>\delta_{T_0}(t)\,</math> powstaje sygnał, który jest przedłużeniem okresowym sygnału <math>x(t)\,</math> z okresem <math>T_0\,</math> . Jeśli sygnał <math>x(t)\,</math> jest sygnałem impulsowym o czasie trwania mniejszym bądź równym <math>T_0\,</math> , to przedłużenie to jest ciągiem dokładnych kopii sygnału <math>x(t)\,</math> powtarzanych co odcinek czasu <math>T_0\,</math> . W przeciwnym przypadku powielone kopie nakładają się na siebie i w sygnale przedłużonym okresowo nie jest zachowany kształt sygnału <math>x(t)\,</math> . | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd17.png]] | |||
|valign="top"| | |||
*Podobnie jak w przypadku sygnałów analogowych, wartość średnia sygnału dyskretnego jest definiowana odmiennie dla różnych klas sygnałów. Definicje te są analogiczne, z tym że całki we wzorach (1.2) –(1.4) są zastąpione odpowiednimi sumami. | |||
*W przypadku sygnałów dyskretnych o nieskończonym czasie trwania ich wartość średnia – tak jak dla sygnałów analogowych – jest definiowana jako wielkość graniczna. Także inne wielkości charakteryzujące tę klasę sygnałów będą definiowane w sensie granicznym. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd18.png]] | |||
|valign="top"| | |||
*Wzory (1.23)–(1.26), określające parametry energetyczne sygnałów dyskretnych, są odpowiednikami wzorów (1.6)–(1.9) definiujących te parametry dla sygnałów analogowych. | |||
*Jeśli energia sygnału dyskretnego <math>x[n]\,</math> , określona wzorem (1.23), spełnia warunek <math>0<E_x<\infty\,</math> , to sygnał taki nazywamy sygnałem o ograniczonej energii. Jeśli moc sygnału dyskretnego <math>x[n]\,</math> , określona wzorem (1.24) lub (1.25), spełnia warunek <math>0<P_x<\infty\,</math> , to sygnał ten nazywamy sygnałem o ograniczonej mocy. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd19.png]] | |||
|valign="top"| | |||
*Zgodnie z przyjętą konwencją we wszystkich przytoczonych tu przykładach sygnałów dyskretnych wyrażamy je jako funkcje czasu <math>n\epsilon \Box\,</math> unormowanego względem okresu próbkowania. | |||
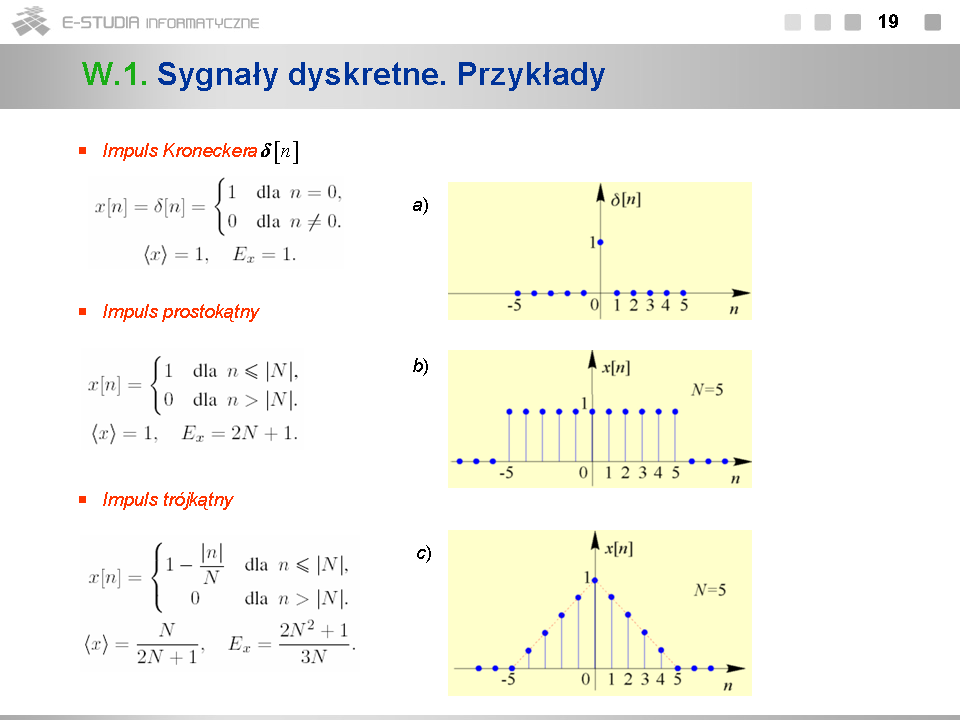
*Impuls Kroneckera <math>\delta[n]\,</math> (rys. a) jest sygnałem dyskretnym przybierającym wartość niezerową i równą <math>1\,</math> jedynie w chwili <math>n=0\,</math> . Pozostałe jego próbki są zerowe. Jest on odpowiednikiem analogowego impulsu Diraca <math>\delta(t)\,</math> , jednak w przeciwieństwie do niego impuls <math>\delta[n]\,</math> jest zwykłą funkcją. Symbol <math>X_0\delta[n-n_0]\,</math> oznacza sygnał dyskretny przybierający jedyną niezerową wartość <math>X_0\,</math> w chwili <math>n_0\,</math> . | |||
*Zarówno impuls Kroneckera, jak i impuls prostokątny (rys. b) oraz impuls trójkątny (rys. c) są przykładami impulsowych sygnałów dyskretnych o ograniczonej energii. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd20.png]] | |||
|valign="top"| | |||
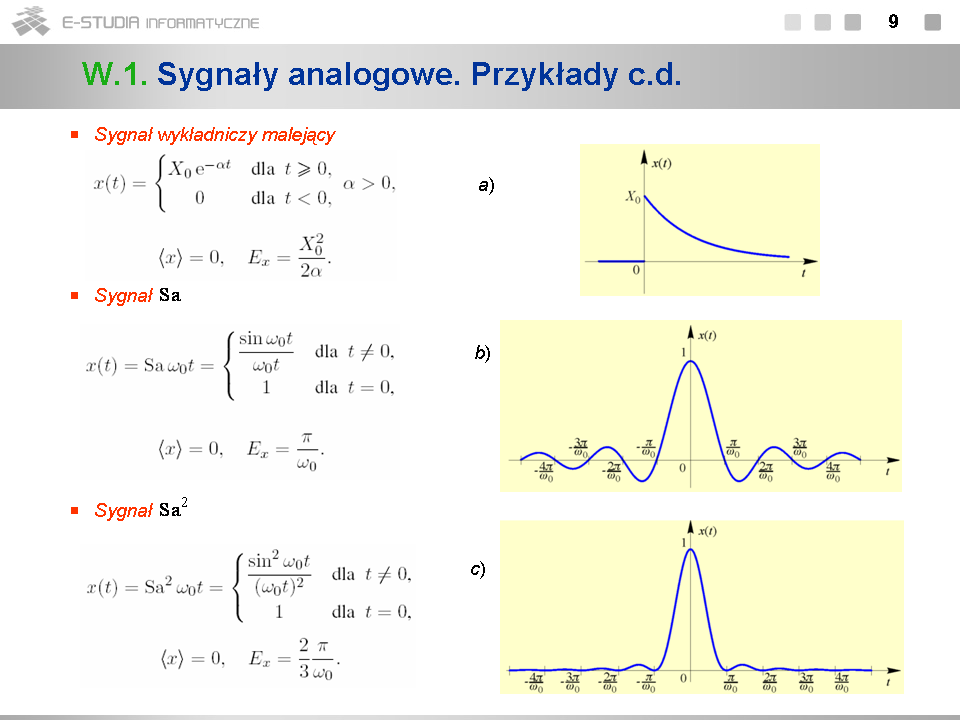
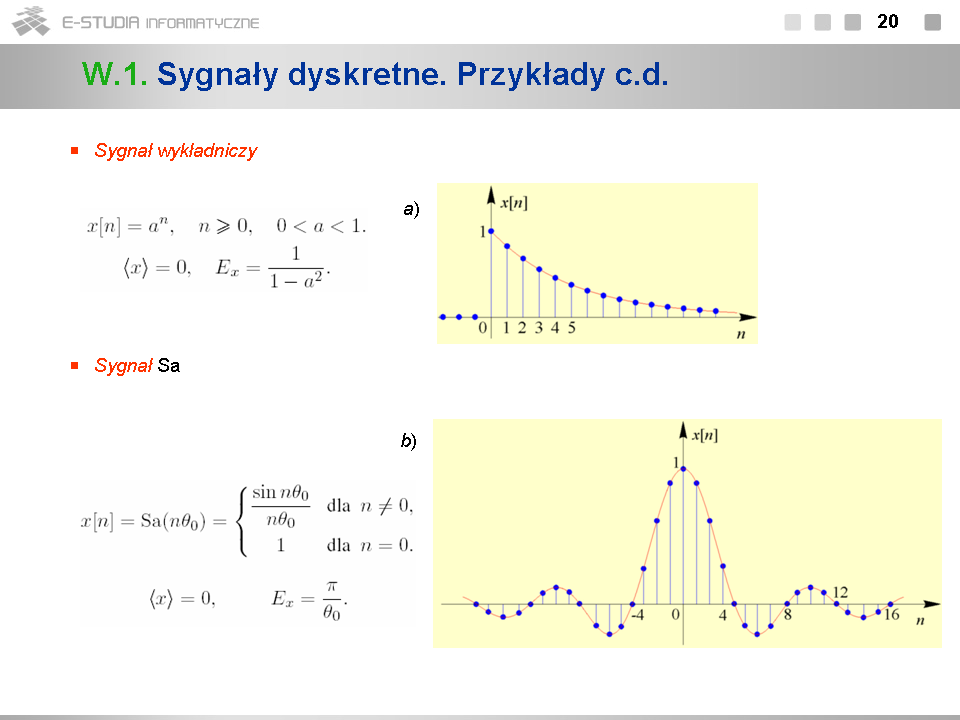
*Sygnały pokazane na rys. a) i b) są przykładami sygnałów dyskretnych o nieskończonym czasie trwania i ograniczonej energii. Są one dyskretnymi odpowiednikami sygnałów analogowych: wykładniczego malejącego oraz <math>Sa\,</math> . | |||
*Parametr <math>\theta_0\,</math> występujący w zapisie dyskretnego sygnału <math>Sa\,</math> ma znaczenie ''pulsacji unormowanej''. W teorii sygnałów dyskretnych normuje się bowiem nie tylko czas, ale także pulsację (częstotliwość) sygnałów. Pojęcie pulsacji unormowanej można wyjaśnić na przykładzie dyskretnego sygnału <math>Sa\,</math> następująco. Sygnał ten można mianowicie traktować jako sygnał otrzymany w wyniku próbkowania analogowego sygnału <math>x(t)=Sa\omega_0 t</math> w chwilach <math>t_n=nT_s\,</math> , gdzie <math>T_s\,</math> jest okresem próbkowania. W wyniku otrzymuje się dyskretny sygnał <math>x[n]=Sa\, n\omega_0 T_s</math> . Wprowadzając bezwymiarowy parametr <math>\theta_0=\omega_0 T_s\,</math> , sygnał ten można zapisać jako <math>x[n]=Sa\, n\theta_0\,</math> . Mówimy, że <math>\theta_0\,</math> jest pulsacją unormowaną względem okresu próbkowania <math>T_s\,</math> . Zauważmy, że wykres dyskretnego sygnału <math>Sa\,</math> z rys. b) został sporządzony dla <math>\theta_0=\pi/4</math> . | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PS_M1_Slajd21.png]] | |||
|valign="top"| | |||
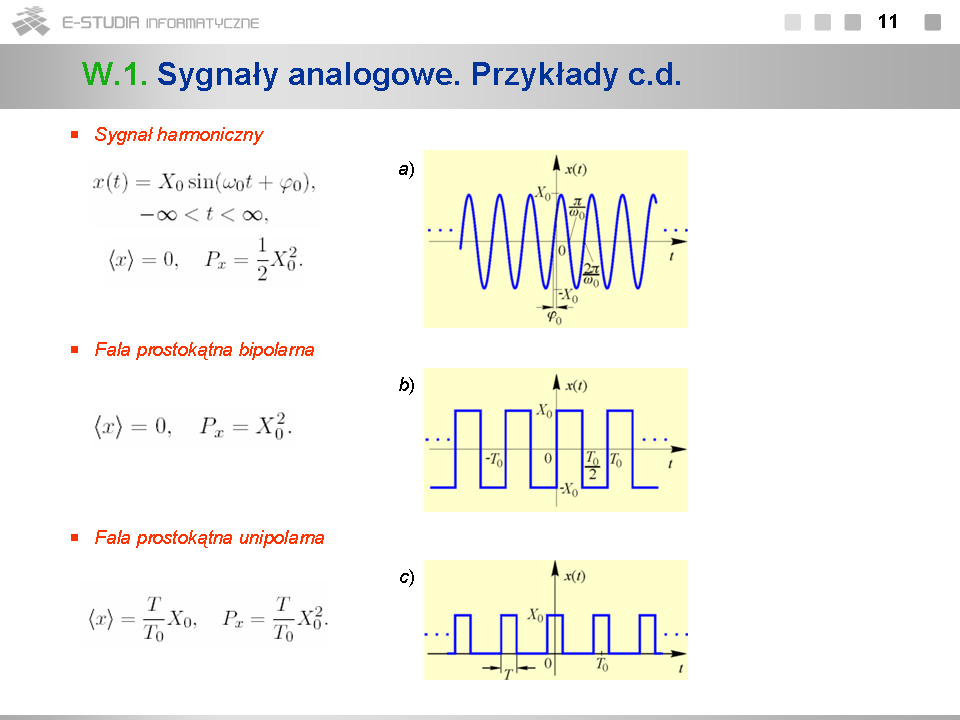
*Sygnały dyskretne pokazane na rys. a)-c) należą do klasy sygnałów o nieskończonym czasie trwania i ograniczonej mocy. | |||
*Dyskretny skok jednostkowy <math>1[n]\,</math> (rys. b) jest odpowiednikiem analogowego skoku jednostkowego <math>1(t)\,</math> . Skok sygnału o dowolną wartość <math>X_0\,</math> przesunięty w czasie o <math>n_0\,</math> próbek można zapisać jako <math>X_01[n-n_0]\,</math> . | |||
*Dyskretny sygnał harmoniczny pokazany na rys. c), nazywany także dyskretną sinusoidą, otrzymujemy w wyniku próbkowania analogowego sygnału harmonicznego <math>x(t)=X_0sin(\omega_0 t+\varphi_0)</math> w chwilach <math>t_n=nT_s</math> . Parametr <math>\theta_0=\omega_0 T_s</math> jest pulsacją unormowaną. Należy podkreślić, że dyskretny sygnał harmoniczny nie musi być sygnałem okresowym zmiennej <math>n\,</math> . Można pokazać, że warunkiem jego okresowości jest, aby liczba <math>2\pi/{\theta_0}\,</math> była liczbą wymierną. Wykres na rys. c) został sporządzony dla <math>\theta_0=\pi/6\,</math> oraz <math>\varphi_0=0\,</math> . W tym przypadku dyskretny sygnał harmoniczny jest oczywiście okresowy. | |||
|} | |||
<hr width="100%"> | |||